完了,对不起各位,这是个意外,我本来计划写完再发的,结果不小心点到提交了


(众所周知,定点转动是解决陀螺类问题的,所以镇楼图当然得是我红色陀螺右方之火大爷啊

在我学习理论力学的过程中,遇到了一个很棘手的问题——定点转动。我使用的是周衍柏先生的理论力学教程,里面推导了欧拉运动学方程组和欧拉动力学方程组,但对于它的求解,书上直言其极其繁琐,并未给出解法。毕竟是一个六个未知数,六个微分方程构成的方程组,真的感觉只能看一眼(真·再看一眼就会爆炸)。对于这样的方程组,工程上一般使用数值解法,而历史上,物理学家们在寻找解析解。最终,在无数工程师与物理学家的努力下,工程上,人类已经可以数值求解定点转动,在计算机上模拟其转动并且在实际上应用,理论上,我们已经在找到了一些可求得解析解的情形。这里我们重点看理论上的求解。电磁学中,可以求较容易求得磁场下电流环的定点转动(也就是拉莫尔情况),它比起后面要说的极其简单,而且也较为出名,可以很容易搜到并且能在几分钟内搞懂,所以这个不讨论了,可以参考理论力学教程,这里写得很详细。我们重点讨论重刚体的定点转动。重刚体定点转动,即仅在重力作用下绕固定点转动。看似很受限,但很快我们会发现可以运用到比较广泛的地方。但是,它的求解极其繁琐,以至于除了翻论文外我甚至找不到完整的求解过程(当然翻论文也很难找到),于是我索性放弃寻找,转而自己推导,并写下此文,希望能帮助更多网友。由初学者个人推导的公式难免有错误,发现了还请指出,谢谢。以下是本文的目录:
前置知识(主要以简要说明+链接的方式呈现)
重刚体定点转动可解情况的分类
对称欧拉潘索情况的求解(这里我将发周衍柏先生的理论力学教程里的推导的图片)
一般的欧拉潘索情况的求解、对称情况的推导及刚体转动的稳定性讨论
拉格朗日泊松情形的求解
刚体一般运动的简要讨论
应用的讨论
好啦,让我们开始正题吧!
一、
以下是本文的前置知识:(我先列知识点,后面会有那里可以学习)
矩阵乘法、矩阵相似对角化等等知识(本文不会出现,但这是前置知识的前置知识);
欧拉角的定义:
;
刚体定点转动的知识:惯量张量、惯量主轴、刚体角动量、转动动能、欧拉运动学方程和动力学方程等等;
接下来会给出这些公式,但在此之前,先做一个规范:
本文中所出现的坐标系有空间中的固定坐标系,其三轴分别为x、y、z轴,对应的单位矢量分别为ex、ey、ez
(我的天用电脑打字好爽,矢量可以直接加粗,再也不用打箭头了)
固连在刚体上的坐标系,其三轴分别是惯量主轴,记为1、2、3轴,对应单位矢量分别为e1、e2、e3
[修改于 9个月27天前 - 2024/01/29 18:20:51]
那么继续第一部分的第三点:
由此规范,我们有:
欧拉运动学方程:
\(\omega_{1} =\dot{\varphi}sin(\theta)sin(\psi)+\dot{\theta}cos(\psi)\) (1.2.1)
\(\omega_{2} =\dot{\varphi}sin(\theta)cos(\psi)-\dot{\theta}sin(\psi)\) (1.2.2)
\(\omega_{3} =\dot{\varphi}cos(\theta)+\dot{\psi}\)(1.2.3)
定点转动角动量:
\(\vec{L} = I_{1}\omega_{1}\vec{e_{1}}+I_{2}\omega_{2}\vec{e_{2}}+I_{3}\omega_{3}\vec{e_{3}}\)(1.3)
定点转动动能:
\(T = \frac{1}{2}(I_{1}\omega_{1}^{2}+I_{2}\omega_{2}^{2}+I_{3}\omega_{3}^{2})\)(1.4)
200字以内,仅用于支线交流,主线讨论请采用回复功能。
那么,由能量守恒\(T + V = E\)得:
\( \frac{1}{2}(I_{1}\omega_{1}^{2}+I_{2}\omega_{2}^{2}+I_{3}\omega_{3}^{2})+ V = E\)(1.5)
由角动量定理\(\dot{\vec{L}} = \vec{M}\)得欧拉动力学公式:
\(I_{1}\dot{\omega_{1}}-(I_{2}-I_{3})\omega_{2}\omega_{3}=M_{1}\)(1.6.1)
\(I_{2}\dot{\omega_{2}}-(I_{3}-I_{1})\omega_{3}\omega_{1}=M_{2}\)(1.6.2)
\(I_{3}\dot{\omega_{3}}-(I_{1}-I_{2})\omega_{1}\omega_{2}=M_{3}\)(1.6.3)
200字以内,仅用于支线交流,主线讨论请采用回复功能。
4.勒让德第一类椭圆积分和一些雅氏椭圆函数的定义:
对\(\int_{0}^{u}\frac{d\xi}{\sqrt{(1-\xi^2)(1-k^2\xi^2)}}\)(1.7)的积分:
若有\(u\in[-1,1]\)和\(k\in[0,1]\)
我们可以换元,令\(\xi = sin(\alpha),u = sin(\phi)\)
即有\(\int_{0}^{\phi}\frac{d\alpha}{\sqrt{1-k^2sin^2(\alpha)}},\phi=arcsin(u)\in[-\frac{\pi}{2},\frac{\pi}{2}]\)(1.8)
这个积分无法用有限的基本初等函数表示,我们将这个积分的结果记作\(F(\phi,k)\)或\(F(arcsin(u),k)\)
可以求得它的级数表示:
\(F(\phi,k)=\phi+\sum_{n = 1}^{\infty}(\frac{(2n-1)!!}{(2n)!!}\int_{0}^{\phi}(ksin(\alpha))^{2n}d\alpha)\)(1.9)
特别地,如果\(\phi = \frac{\pi}{2}\)即\(u=1\),这时(1.9)中求和号内的积分可以积出,此时称为勒让德第一类完全椭圆积分,记作\(K(k)\),有\(K(k) = F(\frac{\pi}{2},k) = \frac{\pi}{2}(1+\sum_{n = 1}^{\infty}(\frac{(2n-1)!!}{(2n)!!}k^n)^2)\)(1.10)
注意上面的!!并不是取完阶乘后再取一次,而是重阶乘,我第一次遇到的时候也以为是取两次,因为卡西欧是这么算的
这个很重要,不知道这个定义看不懂啊!!!(注意!这里的“!!!”不是三重阶乘,只是感叹号,包括本句句首的“!”也只是感叹号 )
)
从上面似乎可以看出\(F(\phi,k)\)的定义域是\([-\frac{\pi}{2},\frac{\pi}{2}]\),但我们总可以使用被积函数的偶函数和周期函数特性,将其定义域延拓至整个实数集,我们有:
\(\int_{0}^{\phi+2c\pi}\frac{d\alpha}{\sqrt{1-k^2sin^2(\alpha)}}=\int_{0}^{\phi}\frac{d\alpha}{\sqrt{1-k^2sin^2(\alpha)}}+4c\int_{0}^{\frac{\pi}{2}}\frac{d\alpha}{\sqrt{1-k^2sin^2(\alpha)}},\phi\in[-\frac{\pi}{2},\frac{\pi}{2}],c\in Z\)
即\(F(\phi+2c\pi,k) = F(\phi,k)+4cK(k),\phi\in[-\frac{\pi}{2},\frac{\pi}{2}],c\in Z\)
不妨设\(k = \frac{114514}{191981}\)

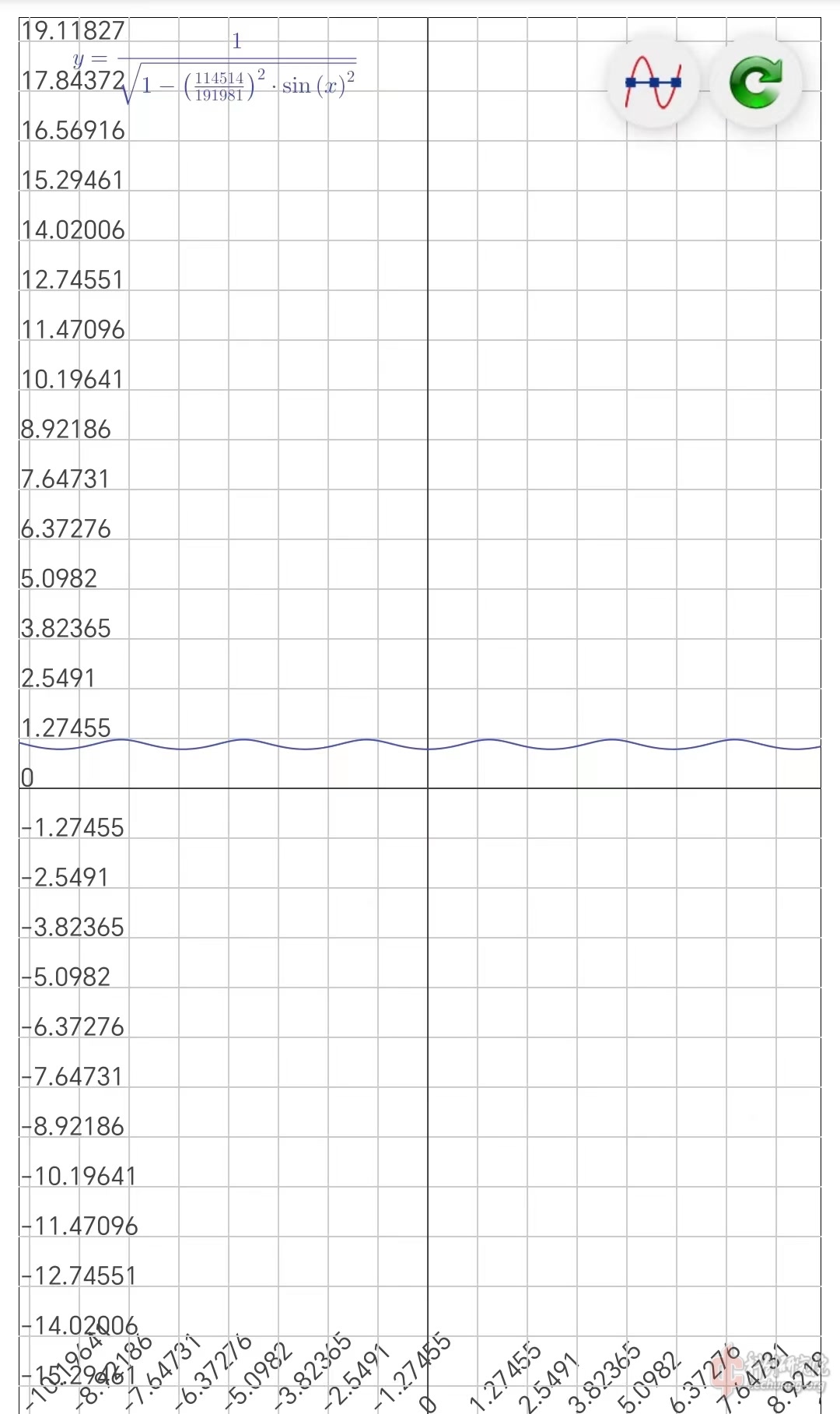
注意!积分(1.7)时仍要确保\(u\in[-1,1]\)
如果我们把k看作参量,可以得到它的反函数,记作\(am(\beta,k)\)
有\(\beta = F(\phi,k),\phi = am(\beta,k)\)(1.11)
定义函数:
\(sn(\beta,k)=sin(am(\beta,k))\)(1.12)
\(cn(\beta,k)=cos(am(\beta,k))\)(1.13)
\(dn(\beta,k) = \sqrt{1-k^2sn^2(\beta,k)}\)(1.14514)
椭圆函数作为数学的一个重要分支,肯定不止这些,我也是在学习理论力学的过程中发现需要用到临时学的,也仅仅刚好够用于求解刚体定点转动,有大佬懂的话还请科普
前置知识点就这些了,一会给出在哪里可以系统学习。
对了,给论坛提一下建议,就是这个公式编辑器能不能做到更加人性化一点呢?就这点我输了一个半小时 (好像还有个鼠标移到上面公式编辑器那个按钮会乱蹦的bug……)
(好像还有个鼠标移到上面公式编辑器那个按钮会乱蹦的bug……)
200字以内,仅用于支线交流,主线讨论请采用回复功能。
接下来说下这些知识可以在哪里系统学习:
线性代数可以参考同济大学的线性代数,我就是看这本的,不过是真的烂啊,把初学者当欧拉还是牛顿啊!bilibili应该有些教程,我没看过,自己参考吧。
欧拉角的定义就看那张图吧,欧拉角在飞控的开发中很重要啊,论坛内外应该都有不少介绍的
刚体力学基础可以参考周衍柏先生的理论力学教程,写得很好,不过硬啃肯定有困难,哔哩哔哩也有一个讲得特别明白的视频,看刚体这一节就行了,前面不看也看得懂,无痛入门啊,链接放这了:XXXXXXXXXXXXXXXXXXXXXXXX/video/BV1xJ411s78q/?spm_id_from=XXXXXXXXXXXXXXXXXXXXXXXXXXick&vd_source=dd348fe7fcf284e0ed80f49ff172deae
这个只是学习必要的知识的话,可以看哔哩哔哩这个视频:物理学杂谈P5.孩子还不会椭圆积分怎么办?稳啦!手把手讲解!_哔哩哔哩_bilibili,系统学习的话参考王竹溪先生和郭敦仁先生的特殊函数概论,但我买来几乎就当个字典用……感觉好难
200字以内,仅用于支线交流,主线讨论请采用回复功能。
二、重刚体定点转动可解出解析解的情况的分类:
欧拉-潘索情况:对刚体的三主轴惯量没有要求,但要求所有力作用于固定点,即\(\vec{M} = \vec{0}\)(2.1)
常见于忽略空气阻力的抛体运动下求解刚体的转动情况等无力矩转动问题,以及陀螺仪的分析,与刚体的一般运动密切相关。
2.拉格朗日-泊松情况:要求三个主轴惯量至少有两个相等,且质心在动力对称轴上且不与固定点重合,常见于陀螺的分析。
3.科凡律夫斯卡雅情况:要求\(2I_{1} =I_{2}=I_{3}\),质心在惯量椭球赤道平面上。由于其求解涉及超几何函数,没学过,也没什么时间去学,再加上其适用情况很窄,故本文不讨论,有大佬懂的话还请补充。
值得说明的是,以上就以及是被找到的全部可解的情况了,其他的情况,都没找到解法,只能数值求解,就连这三种情况,求解方法也完全看不到共性。
我再网上找到的解法都是1.2.的,然而几乎都停在了导出欧拉动力力学方程的特殊情况那一步,这对有好奇心的人十分不友好,所以,接下来会详细阐述它们如何求解,并给出最终结果。在此之前,我们先看一个例子——周衍柏先生的理论力学教程中推导对称欧拉-潘索情况的方法(即1.情况多加一个至少两个主轴惯量相等的条件)。下面会发图。
200字以内,仅用于支线交流,主线讨论请采用回复功能。
三、一种求解对称欧拉-潘索情况的方法和几何法定性分析一般的欧拉-潘索情况的方法,这里就直接发图了。




最后一面下半部分的拉格朗日-泊松情况后面未求出最终解,不用看,我后面会发的
200字以内,仅用于支线交流,主线讨论请采用回复功能。
四、终于进入正题了!开始推导一般的欧拉-潘索情况!
(以下默认\(I_{1}\leq I_{2}\leq I_{3}\)或\(I_{3}\leq I_{2}\leq I_{1}\),或若选取的刚体系不是这样,那么换个系就好了,至于1、3轴到底怎么选取,后面会讲)
由于(2.1),本情况力矩为零,不用管力和坐标的关系,所以我们可以先求解欧拉动力学方程(1.6),得到三轴角速度后再带回欧拉运动学方程(1.2)。由于力矩为零,且力作用再固定点上不做功,故动能和角动量的大小是常量。
由(1.4):\(I_1\omega_1^2+I_2\omega_2^2+I_3\omega_3^2=2T\)(4.1)
由(1.3):\(I_1^2\omega_1^2 +I_2^2\omega_2^2+I_3^2\omega_3^2=\vec L \cdot\vec L =L^2\)(4.2)
接下来我们尝试通过(4.1)(4.2)用\(\omega_2\)表示\(\omega_1\)和\(\omega_3\),至于为什么要这么做,为什么一定要用2轴角速度表示1、3轴角速度,一会儿会说明的(悄悄埋个伏笔)。
求解一个二元一次方程组得到\(\omega_1^2\)和\(\omega_3^2\)的表达式然后开方即可,不过多赘述,有:
\(\omega_1\ =n_1\sqrt{\frac{(2I_3T-L^2)-I_2(I_3-I_2)\omega_2^2}{I_1(I_3-I_1)}}\)(4.3)
\(\omega_3\ =n_3\sqrt{\frac{(L^2-2I_1T)-I_2(I_2-I_1)\omega_2^2}{I_3(I_3-I_1)}}\)(4.4)
以上两式中的n1、n3的值是\(\pm1\),而我为何不用\(\pm\)后面会说,方便计算。由于(4.3)(4.4)式是对整个运动过程都成立的,所以n1、n3的值可以由初始状态\(\omega_{10}\)和\(\omega_{30}\)的方向决定。
那么理顺一下思路,我们以及用2轴角速度表示了1、3轴的角速度,我们可以通过测量初始时刻三个欧拉角的值及其对时间的导数的值得到三轴初始角速度,通过1、3轴初始角速度可以确定n1和n3的值,也就是确定(4.3)(4.4)式中的根式的符号。动能T的大小和角动量L的大小及方向都可以通过(1.4)(1.3)式得出。由于(4.3)(4.4)是全过程成立的,只要我们能够解出2轴角速度随时间的变化关系,我们可以得知任意时刻1、3轴角速度的值,进而求解欧拉运动学方程得出欧拉角随时间的变化,完成本类问题的求解。也就是说,本类问题化成了求解2轴角速度随时间变化关系的问题
我们不是由欧拉动力学方程吗?将(4.3)(4.4)两式带入(1.6.2),又有M2=0,稍微变形一下,可以导出这样一个微分方程:
\(\dot{\omega_2} =\frac{n_1n_3n}{I_2\sqrt{I_1I_3}}\sqrt{((2I_3T-L^2)-I_2(I_3-I_2)\omega_2^2)((L^2-2I_1T)-I_2(I_2-I_1)\omega_2^2)}\)(4.5)
(4.5)中的n的值是\(\pm1\),根据\(I_3-I_1\)的正负确定,因为导出(4.5)时需要求根号下\(I_3-I_1\)的平方,再和\(I_3-I_1\)约分,所以会带符号。
这个微分方程有没有种熟悉的感觉?分离变量后就发现时间那一边可以很简单地积分出来,而角速度那一边,根式在分母,根式里面式四次式,且由两个二次式的乘积组成,而这两个二次式都是一个常数减去另一个常数乘变量的平方形式。这很像第一类椭圆积分欸!于是,我们要尝试用椭圆积分表示2轴角速度。
不过先等等,中间要插入有关在无力矩无约束的情况下刚体绕主轴自由定轴转动的动平衡稳定性问题。至于为什么要先讨论这个,后面就知道了。不过这些要明天再更了啊。
200字以内,仅用于支线交流,主线讨论请采用回复功能。
那么,现在讨论一下无力矩的情况下刚体绕主轴自由转动的平衡稳定性:
我们先假设刚体绕着转动惯量最大的3轴自由转动,1、2轴角速度为零,由欧拉动力学公式(1.6.3)有\(\dot{\omega_3} = 0\),即\(\omega_3= \Omega_3\),\(\Omega_3\)为常量。现在,我们假设由微扰导致1、2轴出现了小角速度\(\omega_1\)
和\(\omega_2\)。注意!它们是小量!那我们对(1.6.1)两侧求导,再将(1.6.2)代入,有:
\(\ddot{\omega_1}+\frac{(I_3-I_1)(I_3-I_2)}{I_1I_2}\Omega_3^2\omega_1=0\)(4.6)
\(\ddot{\omega_2}+\frac{(I_3-I_1)(I_3-I_2)}{I_1I_2}\Omega_3^2\omega_2=0\)(4.7)
不难看出(4.6)(4.7)都是二阶常系数线性常微分方程,并且它们的特征方程都是\(r^2+A_3r=0,A_3 = \frac{(I_3-I_1)(I_3-I_2)}{I_1I_2}\Omega_3^2\)。
由微分方程的知识可以得知,特征方程有两个单实根、一个二重实根、一对共轭复根,也就是特征方程的判别式大于、等于、小于零的情况,分别对应指数函数形式、指数函数与一次函数乘积形式(当然这个特征方程的判别式等于零的话,重根就是零,所以再这个问题中解就是一次函数形式)、三角函数形式的通解,如果要稳定,则1、2轴的角速度应该恒为小量,即只能是三角函数形式。
不难看出,对i轴(i= 1,2,3),Ai>0则稳定,其余情况都不稳定。仿照上文的讨论,不难写出:
\(A_1=\frac{(I_1-I_2)(I_1-I_3)}{I_2I_3}\Omega_1^2\)(4.8.1)
\(A_2=\frac{(I_2-I_1)(I_2-I_3)}{I_1I_3}\Omega_2^2\)(4.8.2)
\(A_3=\frac{(I_3-I_1)(I_3-I_2)}{I_1I_2}\Omega_3^2\)(4.8.3)
由\(I_1\leq I_2\leq I_3\)或\(I_3\leq I_2\leq I_1\)不难得出,三主轴转动惯量都不相等的时候绕转动惯量最大和最小的那个轴转动是稳定的将一直保持定轴转动,绕转动惯量中等的那个轴转动不稳定,将迅速变为定点转动。叫做网球拍定理,名字来源好像是扔网球拍的时候可以观察到这个现象,下面给两张绕轴转动不稳定的动图。


图像来源神十四太空授课,航天员做“扳手翻转”实验,曾被苏联保密10年?_腾讯新闻 (XXXXXX)
里面还有几张动图
好了,那我们看看三轴转动惯量不相同的情况下如果稳定(即绕1、3轴定轴转动)的欧拉角的方程是什么吧,至于两轴转动惯量相同和三轴转动惯量相同后面会作为特例讨论的。
很明显这个时候是定轴转动,进动角和章动角都是常数,而自转角速度是常数。我们知道对固定点角动量的方向再这个情况下不会改变,于是我们不妨取其方向作为转轴吧。由(1.3)知,这个时候角动量与转轴(1、3轴)方向相同。由于欧拉角的缺陷——再章动角为零的情况下,无法分辨自转与进动,这里就按照一般习惯称为自转,毕竟说定轴转动下有进动无自转很奇怪嘛。然后,由于仅一个轴有角速度,不妨取初始自转角为零,那么,对于初始时仅绕1、3轴自由转动,我们分别有最终结果:
\(\varphi = 0,\theta = 0,\psi = \Omega_1t\)(4.9)
\(\varphi = 0,\theta = 0,\psi = \Omega_3t\)(4.10)
很好,这样我们就得到了一般的欧拉-潘索情形在两种情况下的特例。至于为什么要先提一嘴这俩情况,后面会说。
那对于绕2轴的不稳定情况、一开始不绕任何主轴转动的定轴转动和一开始就是定点转动的更加一般的情况呢?且听下回分解
200字以内,仅用于支线交流,主线讨论请采用回复功能。
后面的部分式子是又臭又长,再加上这两天有事,所以从这里开始要更得慢点了
200字以内,仅用于支线交流,主线讨论请采用回复功能。
好的继续:
根据上面的讨论,我们得到了关于2轴角速度的微分方程(4.5)
为了搞成第一类椭圆积分的形式,我们希望吧\(2I_3T-L^2\)、\(L^2-2I_1T\)提取出去,所以我们必须先讨论它们的大小,结合(1.3)(1.4)式,代入初始角速度,我们有:
\(2I_3T-L^2 = I_1(I_3-I_1)\omega_{10}^2 + I_2(I_3-I_2)\omega_{20}^2\)(4.11)
\(L^2-2I_1T = I_2(I_2-I_1)\omega_{20}^2 + I_3(I_3-I_1)\omega_{30}^2\)(4.12)
好了先回收一个伏笔,记得为啥一定要用2轴角速度表示1、3轴角速度不?就是这个原因,这样推导出来由各主轴惯量之间的大小关系可以一眼看出,不管1、3轴转动惯量大小如何,\(2I_3T-L^2\)和\(L^2-2I_1T\)二者同号!
之前说过,先讨论主轴惯量不等的情况,那么如果\(2I_3T-L^2\)等于零,\(L^2-2I_1T\)不等于零,那么由(4.11),(4.12)可知1、2轴初始角速度为零,仅3轴初始角速度不为零,这不就是前面说到绕3轴定轴转动吗?那么定点转动退化为定轴转动,那么运动规律就是(4.10)了!(看到没第二个伏笔也回收了

反之,如果\(2I_3T-L^2\)不等于零,\(L^2-2I_1T\)等于零,那么由(4.11),(4.12)可知2、3轴初始角速度为零,仅1轴初始角速度不为零,运动规律也就是(4.9)
那万一\(2I_3T-L^2\)和\(L^2-2I_1T\)都等于零呢?那更简单了,由(4.11),(4.12)可知,1、2、3轴初始角速度都为零,角速度矢量各个分量都为零,那么初始角速度不就零矢量了吗?也就是这个情况下刚体静止,压根就没动!即:
\(\varphi = 0,\theta = 0,\psi = 0\)(4.13)
这个情况相当简单,一看就知道了,所以当三轴角速度为零时刚体一定保持静止,运动规律一定是(4.13),和它的三个主轴惯量是否相同无关,所以后面讨论由主轴惯量相同的特殊情况的时候,就不考虑这种情况了。
当然,我知道大家不是想看这么简单的特殊情况,那么接下来就讨论\(2I_3T-L^2\)和\(L^2-2I_1T\)都不等于零的最一般的情况。
先把(4.5)\(2I_3T-L^2\)和\(L^2-2I_1T\)提出来,然后把根式移到左侧分母,把dt移到右侧,利用n1n3的性质,有:
\(n_1n_3n\frac{\sqrt{(2I_3T-L^2) (L^2-2I_1T)}}{I_2\sqrt{I_1I_3}}dt = \frac{d\omega_2}{\sqrt{(1-\frac{I_2(I_3-I_2)}{2I_3T-L^2}\omega_2^2)(1-\frac{I_2(I_2-I_1)}{L^2-2I_1T}\omega_2^2)}}\)(4.14)
更像第一类椭圆积分了对吧?
似乎只用换给变量再积分就可以了。但是,我们还要注意2轴角速度平方前面的系数取值范围的问题,毕竟前文说了,必须再0到1之间。这个下午再发
200字以内,仅用于支线交流,主线讨论请采用回复功能。
再进一步讨论前,先设置几个变量,一会看起来舒服点。令:
\(P =n_1n_3n\frac{\sqrt{(2I_3T-L^2)(L^2-2I_1T)}}{I_2\sqrt{I_1I_3}}\)(4.15)
\(Q =\sqrt{\frac{I_2(I_3-I_2)}{2I_3T-L^2}} \)(4.16)
\(R =\sqrt{\frac{I_2(I_2-I_1)}{L^2-2I_1T}} \)(4.17)
则,(4.14)可改写为\(Pdt = \frac{d\omega_2}{\sqrt{(1-Q^2\omega_2^2)(1-R^2\omega_2^2)}}\)(4.18)
由定义可知,P、Q、R三者根号下的部分都大于零,所以为实数。
200字以内,仅用于支线交流,主线讨论请采用回复功能。
由定义,我们可以发现,Q、R都大于零,这样就满足条件了。如果我们要把(4.18)化为(1.7)形式,那么很自然的想法是两边同乘Q或R,然后右边塞到微分里面,换个元,那么参数k就应该是Q/R或R/Q了。但是要满足k在0到1之间,积分变量要在-1到1之间,所以需要讨论……吗?别忘了,我们还没有定义1、3轴,现在给出1、3轴的定义:
1、3轴转动惯量及初始角速度应该满足\(Q\ge R\),即\( (I_3-I_2)(L^2-2I_1T)\ge(I_2-I_1)(2I_3T-L^2)\),代入初始值,有:
\((I_3-I_2)I_3\omega_{30}^2 \ge (I_2-I_1)I_1\omega_{10}^2\)(4.19)
我们有\(\frac{R}{Q}\le 1\),那么我们就两端同乘Q,有:
\(QPdt = \frac{dQ\omega_2}{\sqrt{(1-Q^2\omega_2^2)(1-(\frac{R}{Q})^2Q^2\omega_2^2)}}\)(4.20)
这里我们再定义:
\(\lambda = QP = n_1n_3n\sqrt{\frac{(I_3-I_2)(L^2-2I_1T)}{I_1I_2I_3}}\)(4.21)
\(k =\frac{R}{Q} = \sqrt{\frac{(I_2-I_1)(2I_3T-L^2)}{(I_3-I_2)(L^2-2I_1T)}}\)(4.22)
\(\xi = Q\omega_2 = \sqrt{\frac{I_2(I_3-I_2)}{2I_3T-L^2}}\omega_2\)(4.23)
于是,由(4.19),我们有:
\(\int_0^t\lambda dt = \int_{\xi(0)}^{\xi(t)}\frac{d\xi}{\sqrt{(1-\xi^2)(1-k^2\xi^2)}}\)(4.24)
这样就可以直接积分了……吗?不,我们虽然保证了\(k_1\in[0,1]\),但\(\xi_1\)的范围还不知道,由于它的值是常量,我们不妨代入初始值。我们希望它是在-1与1之间的,这样我们就可以直接用第一类椭圆积分了。现在我们来证一下。
显然\(\xi_1\)大于等于零,所以要证的只有它小于等于一。
结合(1.3)(1.4),移项有:\(I_2(I_3-I_2)\omega_2^2 = (2I_3T-L^2)-I_1(I_3-I_1)\omega_1^2\)(4.25)
代入即有\(\xi = \sqrt{1-\frac{I_1(I_3-I_1)\omega_1^2}{2I_3T-L^2}}\)(4.26)
(4.26)中根式里面减去的那一项由前面的讨论和定义可知,一定大于等于零,所以显然\(\xi\in[0,1]\)
现在我们终于可以放下一切顾虑愉快地积分了!
综上所述,我们有(4.24):
\(\int_0^t\lambda dt = \int_{\xi(0)}^{\xi(t)}\frac{d\xi}{\sqrt{(1-\xi^2)(1-k^2\xi^2)}}\)
当1、3轴取向满足\((I_3-I_2)I_3\omega_{30}^2 \ge (I_2-I_1)I_1\omega_{10}^2\)时:
\(\lambda = n_1n_3n\sqrt{\frac{(I_3-I_2)(L^2-2I_1T)}{I_1I_2I_3}}\)(4.27)
\(k = \sqrt{\frac{(I_2-I_1)(2I_3T-L^2)}{(I_3-I_2)(L^2-2I_1T)}}\)(4.28)
\(\xi = \sqrt{\frac{I_2(I_3-I_2)}{2I_3T-L^2}}\omega_2\)(4.29)
200字以内,仅用于支线交流,主线讨论请采用回复功能。
从(4.24)中,利用勒让德第一类椭圆积分,两端积分可以解出\(\xi\),即:
\(\lambda t = F(arcsin(\xi(t)),k)-F(arcsin(\xi(0)),k)\)(4.30)
利用雅各比椭圆函数,有:
\(\xi(t) = sn(\lambda t+F(arcsin(\xi(0)),k),k)\)(4.31)
由于\(F(arcsin(\xi(0)),k)\)是常量,不妨定义为\(\mu\),即
\(\mu = F(arcsin(\xi(0)),k)=F(arcsin(\sqrt{\frac{I_2(I_3-I_2)}{2I_3T-L^2}}\omega_{20}),\sqrt{\frac{(I_2-I_1)(2I_3T-L^2)}{(I_3-I_2)(L^2-2I_1T)}})\)(4.32)
这样(4.31)可以进一步简化为:
\(\xi(t) = sn(\lambda t+\mu,k)\)(4.33)
那么由(4.29),(4.33)及定义可得到二轴角速度随时间的变化关系:
\(\omega_2(t) = \sqrt{\frac{2I_3T-L^2}{I_2(I_3-I_2)}}sn(\lambda t+\mu,k)\)(4.34)
200字以内,仅用于支线交流,主线讨论请采用回复功能。
继续之前,先梳理一波思路,我们已经得到了2轴角速度随时间的变化关系,只用代入(4.3)(4.3)便可知道三个轴各自角速度随时间的变化关系,代入欧拉运动学方程(1.6)即可得到欧拉角随时间的变化关系,也就是我们要的结果。虽然很多新设的参量,但是理论上看,一般的问题,模型是简单的,特殊的问题,可以计算这些参量的值,也很简单。实际应用上看,也可以方便地测量出各参量进而应用。当然,还有个重点,这个sn函数,它是什么?实际上雅各比椭圆函数是有级数表达式的,这么看甚至比还需要用积分表述的勒让德第一类椭圆积分还要简单。但是,我之前也说了,我也是看理论力学的时候搞不明白才学的一点皮毛的皮毛,所以我根本不会,而且近期学习计划都更偏向物理,这些东西可能几年后我才会学,所以,雅各比椭圆函数的级数表达式和证明请参考王竹溪先生和郭敦仁先生的特殊函数概论。我就不发了,因为太恶心且涉及好多书前面内容的参量。不过纵使它很恶心,再理论上的估算和实际应用上还是比较方便的,因为雅各比椭圆函数有周期性(这个由定义很容易看出sn、cn的周期为4K(k),dn的周期为2K(k))而且的收敛比较快,所以实际应用中通过测量研究对象即可算出k和K(k),然后级数一般取前几项就够了,用程序实现很简单的。我下面放一下前几项的图,图片来自于雅可比椭圆函数函数的幂级数展开式怎么证明? - 知乎 (XXXXXXXXX)
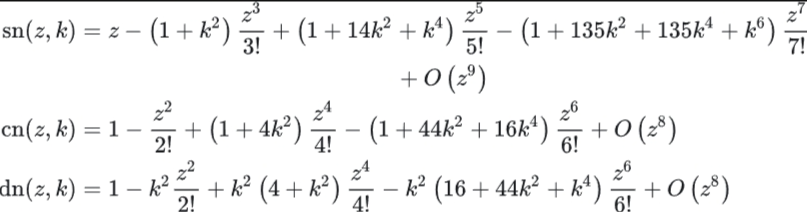
200字以内,仅用于支线交流,主线讨论请采用回复功能。
坏了……出了点小问题,我一开始自己算的时候没有考虑前面说的一个讨论,写的时候突然发现,然后现场讨论了下,以为不同情况用不同的参量就没问题了,可是现在才发现似乎并不是这样,因为1、3轴角速度函数名不同……那么后面得继续讨论了……
200字以内,仅用于支线交流,主线讨论请采用回复功能。
昨天出了的那个问题我终于搞定了。是这样的,我之前写在笔记本上,漏了一个很小的点,即正负号,但是这牵扯出了一个很大的麻烦。我昨天写上来的时候才发现,我昨天无法解释,想了好久,又去知网搜论文,但完全没有这个方向的研究。今天上午终于完全想通了,发现原来答案没错,但是过程有问题。这个插曲让我发现这样把自己的发现记录发到论坛还是有很大作用的,重新梳理思路真的有利于发现纠正错误,更有利于加深对物理的理解。我现在不在家,用的是手机,我决定今晚回家就先把这一步本来错误的过程发出来(当然比起说是错误,更像是不严谨,只是有几步没证就出来了),然后再补充为什么答案是正确的。(对了,这件事情让我更加认识到物理是美的,之前我搞出的结果确实简洁美观,后面发现过程不严谨以为是错的,搞出来其他的结果都很丑而且都是错的,最后确实证明出来前面漂亮的结果是正确的)
200字以内,仅用于支线交流,主线讨论请采用回复功能。
讨论前先说明一下,为防止混淆,第四章从此就只在雅各比椭圆函数内部使用自定义的参数了,也只使用\(\lambda、\mu、k\)这三个了。
由于\((I_3-I_2)I_3\omega_{30}^2\ge(I_2-I_1)I_1\omega_{10}^2\)
由(4.34)将其代入(4.3),有:\(\omega_1(t) = n_1\sqrt{\frac{2I_3T-L^2}{I_1(I_3-I_1)}}\sqrt{1-sn^2(\lambda t+\mu,k)}\)(4.35)
由定义得:
\(\omega_1(t) = \sqrt{\frac{2I_3T-L^2}{I_1(I_3-I_1)}}cn(\lambda t+\mu,k)\)(4.36)
那么代入(4.4),有:\(\omega_3(t) = n_3\sqrt{\frac{L^2-2I_1T}{I_3(I_3-I_1)}}\sqrt{1-(\sqrt{\frac{(I_2-I_1)(2I_3T-L^2)}{(I_3-I_2)(L^2-2I_1T)}})^2sn^2(\lambda t +\mu,k)}\)(4.37)
不难发现,根式里面,第二个因式sn2前面的系数,正是k2!由定义,即有:
\(\omega_3(t) = n_3\sqrt{\frac{L^2-2I_1T}{I_3(I_3-I_1)}}dn(\lambda t +\mu,k)\)(4.38)
总结一下,我们现在便得出了三轴角速度随时间的变化关系,胜利就在眼前啊!
但是,有人可能注意到两个问题,也就是我前文说的不严谨的地方,一是为什么默认n1、n3是常量?二是为什么(4.37)式排除n3一定大于零,而(4.38)式可以小于零也可以大于零而不加绝对值,然后n1为什么没了?好的,一会儿会讨论这个,狡辩一下,这么做的原因是表述更加方便,如果这里直接用正确的方法说的话表述太麻烦了,不如先这样推出来,再说明下为什么(好吧最重要的原因是我自己推的时候犯了两个低级错误结果算出来是对的,干脆就先这么写了)
结论:
\(\omega_1(t) = \sqrt{\frac{2I_3T-L^2}{I_1(I_3-I_1)}}cn(\lambda t+\mu,k)\)(4.39.1)
\(\omega_2(t) = \sqrt{\frac{2I_3T-L^2}{I_2(I_3-I_2)}}sn(\lambda t+\mu,k)\)(4.39.2)
\(\omega_3(t) = n_3\sqrt{\frac{L^2-2I_1T}{I_3(I_3-I_1)}}dn(\lambda t +\mu,k)\)(4.39.3)
以上(4.39)式即为三轴角速度随时间的变化关系,有没有感觉特别美?刚好对应了三个主要的雅各比椭圆函数等等……感觉有千丝万缕的联系。
200字以内,仅用于支线交流,主线讨论请采用回复功能。
在讨论之前,先说明一件事,就是物理和数学不同的地方,在于物理是反映世界的,所以有些数学上合理的在物理反而不合理,比如你不可能说某个质点的运动轨迹是y = D(x)吧?毕竟狄利克雷函数这么抽象,现实中物体的运动不可能出现这种情况。所以去看看数理方法,里面就经常会出来一些因为不符合物理就舍去什么的情况,这在物理里面是合理的,但数学上应该就是逼疯数学家的操作了。
那么我们可以说明上文说的第二个问题了,确实是不应该加绝对值的,否则在函数值为零的情况下,该点左右导数不同,该点不可导!在数学上也许没什么,但是物理上麻烦就大了,相当于这个点的角加速度出现了突变,看起来没啥,但是往欧拉动力学方程里面一代就会发现这个时候,另外两个轴的角速度的乘积发生了突变!也就是另外两个轴的角加速度至少一个要无穷大!这在数学里可以说句无穷不存在什么的,但是物理里面出现无穷大可是有大问题的!也就是说这种解必须舍去。
那既然不能加绝对值,那怎么解释实际上1、3轴角速度其中一个可以与初始方向不同,而设的时候却假设了必须相同?这就要扯到第一个问题了。实际上n1、n3可以改变符号即从-1变为+1或从+1变为-1!但是都可以改变吗?什么时候改变?显然如果能变,那么只能在角速度值为零的时候改变,毕竟角速度必须连续变化,角速度不为零的时候改变符号意味着角速度突变,意味着角加速度为无穷大。
在讨论到底改变不改变之前,我们先来看看对于和这俩量无关的2轴角速度会怎么变。由于n1、n3如果都变,那么\(\lambda\)肯定不变,最后结果也肯定不变,因为负负得正嘛。那如果只改变一个呢?那么
\(\lambda\)将会变成类似方波的形式,积分后则是类似三角波的形式,如图

那么2轴角速度积分出来在sn函数里面的则是这样的一个三角波函数代替一次函数。由sn函数和cn函数的定义可知,cn函数为零,也就是符号可能改变时,sn函数在最大值或最小值处。也就是说这个时候sn函数里面的那部分的值只能在sn函数的某个最大值和它相邻一个最小值之间,匀速随时间改变,遇到最值则改变随时间改变的方向。注意到sn函数的周期性,那么2轴角速度的值则不会改变,如图,完全相当于原来的形式。

这也是为什么我错误的过程可以推出正确的结论。因为不过n1和n3到底变不变,怎么变,2轴角速度的表示都不变,推出来的1、3都是那个形式,最多只差正负号。而正负号的改变由上文的讨论,为保证角速度为零时可导,只能且必须在角速度为零时改变。原来直接从根式里面开出来就需要绝对值,绝对值对连续的函数不就相当于在函数值为零处改一次符号吗?负负得正了,符号改回去了!所以绝对值符号和n1可以去掉了,n3可以当做常量取初始值了!
这也就解决了那两个问题。
为方便,往后就按照(4.39)的形式,不带绝对值,且把n3当成常量了,因为结果是完全等价的。
200字以内,仅用于支线交流,主线讨论请采用回复功能。
好了,至此欧拉动力学方程的求解就完成了,接下来求解欧拉运动学方程。我们现在尝试使用角速度来表示欧拉角。考虑到角动量守恒,我们取角动量L的方向作为空间坐标系z轴,然后利用欧拉角分解到1、2、3轴方向,通过与角速度的关系便可求出欧拉角。
我们可以直接分解得出三轴角动量的值。当然,考虑到L与进动角对时间的导数\(\dot{\varphi}\)方向相同,也就是说,角动量分解到1、2、3轴后L前系数与角速度分解到1、2、3轴后\(\dot{\varphi}\)前的系数一致。利用这点,我们可以得出:
\(I_1\omega_1 = Lsin(\theta)sin(\psi)\) (4.40.1)
\(I_2\omega_2 = Lsin(\theta)cos(\psi)\) (4.40.2)
\(I_3\omega_3 = Lcos(\theta)\)(4.40.3)
先捏软柿子,从(4.40.3)可以显然看出章动角,有\(cos(\theta) = \frac{I_3\omega_3}{L}\)。
我们知道,\(\theta \in [0,\pi]\),而arccos函数的值域也是\([0,\pi]\),所以我们可以用arccos函数唯一确定一个\(\theta\),即:\(\theta = arccos(\frac{I_3\omega_3}{L})\)(4.41)
同时,看看(4.40.1)和(4.40.2)的形式,可以利用正弦余弦平方和为一的特性。(4.40.1)和(4.40.2),先平方再相加,开方,利用\(\theta \in [0,\pi]\),正弦大于零,有:
\(sin(\theta) = \frac{\sqrt{I_1^2\omega_1^2+I_2^2\omega_2^2}}{L}\)(4.42)
其实我们不需(4.42)也可确定章动角,但是后面要用它,所以一并求出来了。也可以直接由(4.41)式,利用三角函数正余弦平方和为一及这种情况下正弦大于零的特性求出。
接下来看自转角(4.40.1)和(4.40.2)相除即可求出自转角的正切值,周衍柏先生的理论力学上便是这么求的对称陀螺的。但是那是因为对称情况下,角速度之比也刚好有正切出现,可以直接通过诱导公式和角的范围确定,而一般情况下并不具备这种条件,再加上arctan函数的值域并不是\([0,2\pi]\),所以我们计划求出自转角的正弦和余弦值,并通过它们确定自转角的值。有:
\(sin(\psi) = \frac{I_1\omega_1}{Lsin(\theta)} = \frac{I_1\omega_1}{\sqrt{I_1^2\omega_1^2+I_2^2\omega_2^2}}\)(4.43)
\(cos(\psi) = \frac{I_2\omega_2}{Lsin(\theta)} = \frac{I_2\omega_2}{\sqrt{I_1^2\omega_1^2+I_2^2\omega_2^2}}\)(4.44)
通过(4.43)(4.44)可以唯一确定自转角\(\psi\)。
最后搞最麻烦的进动角\(\varphi\),由(1.2.3)可以得出
\(\dot{\varphi} = \frac{\omega_3-\dot{\psi}}{cos(\theta)}\)(4.45)
看样子这个就必须积分了,我们先确定被积函数,利用(4.41),(4.43),(4.44)和三角函数微分的性质,有
\(\dot{\varphi} = \frac{L}{I_3}-\frac{L\sqrt{I_1^2\omega_1^2+I_2^2\omega_2^2}}{I_2I_3\omega_2\omega_3}\frac{d}{dt}[\frac{I_1\omega_1}{\sqrt{I_1^2\omega_1^2+I_2^2\omega_2^2}}]\)(4.46)
积分,有:
\(\varphi = \frac{L}{I_3}t-\frac{I_1L}{I_3I_2}\int_0^t\frac{\sqrt{I_1^2\omega_1^2+I_2^2\omega_2^2}}{\omega_2\omega_3}\frac{d}{dt}[\frac{\omega_1}{\sqrt{I_1^2\omega_1^2+I_2^2\omega_2^2}}]dt+\varphi_0\)(4.47)
代入角速度便可得到最终结果,一会发出来。
这几天有点忙,可能更得要慢一点
200字以内,仅用于支线交流,主线讨论请采用回复功能。
我现在发现了三个东西,一是n有一个最后要去掉,二是其实本文可以不用分类讨论,只需要在最初根据不同情况改一下坐标轴取向即可,三是我发现我之前的问题真的太多了,又发现科创可以编辑回复。所以我打算在前文直接改正回来,特在此说明,以防误导了大家。
200字以内,仅用于支线交流,主线讨论请采用回复功能。
终于,我们得到了欧拉潘索情形的结果了
\(\varphi = \frac{L}{I_3}t-n_3L\sqrt{\frac{I_1(I_3-I_2)}{I_2I_3(L^2-2I_1T)}}\int_0^t\frac{\sqrt{I_1cn^2(\lambda t+\mu,k)+\frac{I_2(I_3-I_1)}{I_3-I_2}sn^2(\lambda t+\mu,k)}}{dn(\lambda t+\mu,k)sn(\lambda t+\mu,k)}\frac{d}{dt}(\frac{cn(\lambda t+\mu,k)}{\sqrt{I_1cn^2(\lambda t+\mu,k)+\frac{I_2(I_3-I_1)}{I_3-I_2}sn^2(\lambda t+\mu,k)}})dt+\varphi_0-2a\pi\)(4.48.1)
(a = 0,1,2……,a是使得\(\varphi\in[0,2\pi]\)自然数)
\(\theta = arccos(\frac{n_3}{L}\sqrt{\frac{I_3(L^2-2I_1T)}{I_3-I_1}}dn(\lambda t+\mu,k))\)(4.48.2)
当\(cn(\lambda t+\mu,k) > 0\)时:
\(\psi = arccos(\sqrt{I_2}\frac{sn(\lambda t+\mu,k)}{\sqrt{I_1cn^2(\lambda t+\mu,k)+\frac{I_2(I_3-I_1)}{I_3-I_2}sn^2(\lambda t+\mu,k)}})\)(4.48.3.1)
当\(cn(\lambda t+\mu,k) < 0\)时:
\(\psi = 2\pi-arccos(\sqrt{I_2}\frac{sn(\lambda t+\mu,k)}{\sqrt{I_1cn^2(\lambda t+\mu,k)+\frac{I_2(I_3-I_1)}{I_3-I_2}sn^2(\lambda t+\mu,k)}})\)(4.48.3.2)
当\(cn(\lambda t+\mu,k) = 0\)时:自转角与dt前后的自转角仅差一小量,可确定为0还是\(\pi\)
以上便是欧拉潘索情形的一般解,其中参量的值在(4.27)(4.28)(4.32)中确定。
200字以内,仅用于支线交流,主线讨论请采用回复功能。
我们现在从(4.48)中讨论特殊情况。
先还是假定三轴转动惯量都不等。
如果初始角速度仅2轴不为零,代入,可以发现什么事情都不会发生,转动还是复杂的定点转动形式。
如果初始角速度仅一轴(不是2轴)不为零,代入,由(4.19),我们应取该轴为3轴。而此时,R为零,即k=0,此时,由雅各比椭圆函数定义,sn函数退化为sin函数,cn函数退化为cos函数,dn函数退化为1,此时代入(4.48.2),由于此时\(L^2-2I_1T = I_3(I_3-I_1)\omega_{30}^2\),\(L=I_3\omega_{30}\)应有:
\(\theta = arccos(n_3)\)(4.49)
即\(\theta = 0\)(当n3=1时)或\(\theta = \pi\)(当n3= -1时)
此时\(sin(\theta) = 0\)
代入(4.40.1)和(4.40.2)可以发现是恒等式,也就是说自转角任意。这也是前文说的欧拉角的缺陷,章动角为零时无法分辨自转和进动。依旧按习惯,取\(\psi\)使得刚体有自转无进动。
由(4.45)得,\(\dot{\psi} = \omega_{30}\)(4.50)
积分,不妨取坐标使得初始自转角为零,进动角为零,即有:
\(\varphi = 0,\theta = 0,\psi = \omega_{30}t\)(4.51)
显然,上式即为(4.9)(4.10)。
这也就验证了网球拍定理
再讨论(4.19)取等号的情况,即Q=P,k=1
由雅各比椭圆函数定义,此时……好像也没啥特殊性质……只是现在(4.48)可以用基本初等函数表示出来了,有兴趣的可以试试
200字以内,仅用于支线交流,主线讨论请采用回复功能。
接下来讨论对称欧拉陀螺的情形的一般情况。由定义,此时只可能是一个轴转动惯量与2轴转动惯量相等。由(4.19)应取该轴为1轴。
即\(I_1=I_2\)。
那么由(4.28),k=0,sn、cn、dn函数分别退化为sin、cos、1,故三轴角速度不改变。
由(4.12),仍有\(L^2-2I_1T = I_3(I_3-I_1)\omega_{30}^2\),那么代入(4.48.2),有:
\(\theta = arccos(\frac{I_3\omega_{30}}{L})\)(4.52)
可见章动角为一个常数,且一般不为零。
由(4.48.3),\(cos(\psi) = sin(\lambda t+\mu),sin(\psi) = cos(\lambda t+\mu)\)(4.53),
易知\(\psi = \frac{\pi}{2}-(\lambda t+\mu)-2a_{\psi}\pi,a_{\psi}=0,1,2……\)(4.54)
由(4.27)(两个符号和对应绝对值,消掉了):
\(\lambda = \frac{I_3-I_1}{I_1}\omega_{30}\)(4.55)
由(4.32)(k=0,积分一次即可):
\(\mu = arcsin(\frac{\omega_{20}}{\sqrt{\omega_{10}^2+\omega_{20}^2}})\)(4.56)
故:
\(\psi = \frac{\pi}{2}-(\frac{I_3-I_1}{I_1}\omega_{30}t+arcsin(\frac{\omega_{20}}{\sqrt{\omega_{10}^2+\omega_{20}^2}}))-2a_{\psi}\pi,a_{\psi}=0,1,2……\)(4.57)
可知自转是匀速的。
代入(4.45),积分,有:\(\varphi = \frac{L}{I_1}t+\varphi_0-2a_{\varphi}\pi,a_{\varphi}=0,1,2……\)(4.58)
总结下,对称欧拉陀螺的运动规律:
\(\varphi = \frac{L}{I_1}t+\varphi_0-2a_{\varphi}\pi,a_{\varphi}=0,1,2……\)(4.59.1)
\(\theta = arccos(\frac{I_3\omega_{30}}{L})\)(4.59.2)
\(\psi = \frac{\pi}{2}-(\frac{I_3-I_1}{I_1}\omega_{30}t+arcsin(\frac{\omega_{20}}{\sqrt{\omega_{10}^2+\omega_{20}^2}}))-2a_{\psi}\pi,a_{\psi}=0,1,2……\)(4.59.3)
其中常数均是保证欧拉角在其定义域内的。
与前文书中照片对比,发现是一样的,只是后面为满足欧拉角定义域加了几个常数。
这种情况下,进动和自转都是匀速的,且无章动,称之为规则进动。
讨论一下,若仅1或2轴角速度不为零,代入可知,章动角为\(\frac{\pi}{2}\),即自转的同时在赤道平面内进动。当然,章动角为何不为零也是欧拉角的缺陷,实际上是稳定的旋转,前文讨论网球拍定理的时候,令两轴转动惯量相等,可以发现为一次函数,有限时间偏移内仍为小量,大家可以扔个矿泉水瓶看看。
而若仅三轴角速度不为零,由(4.59.2)有:
\(\theta = arccos(1)=0\)(4.60)
即章动角为零,始终绕着角动量方向也就是3轴旋转。此时,还是欧拉角的缺陷,自转和进动似乎都有,我们还是按照习惯取有自转无进动,并取初始自转角为零,即此时:
\(\varphi = 0,\theta = 0,\psi = \omega_{30}t\)(4.61)
200字以内,仅用于支线交流,主线讨论请采用回复功能。
最后,再讨论最特殊的情况,三轴转动惯量都相等的情况,不妨把转动惯量都记作\(I\),代入(4.59)。
\(\varphi = \frac{L}{I}t+\varphi_0-2a_{\varphi}\pi,a_{\varphi}=0,1,2……\)(4.62.1)
\(\theta = arccos(\frac{I\omega_{30}}{L})\)(4.62.2)
\(\psi = \frac{\pi}{2}-(arcsin(\frac{\omega_{20}}{\sqrt{\omega_{10}^2+\omega_{20}^2}}))-2a_{\psi}\pi,a_{\psi}=0,1,2……\)(4.62.3)
这个就没啥讨论的必要了,角速度矢量不论向哪都一样,据惯量椭球的知识,可以证明,此时任意方向的转动惯量都为\(I\),这个就参考理论力学了,且此时角动量矢量方向角速度矢量方向相同,所以可以取这个方向为3轴,并记初始自转角为零。所以,一定有:
\(\varphi = 0,\theta = 0,\psi = \omega_{30}t\)(4.63)
200字以内,仅用于支线交流,主线讨论请采用回复功能。
芜湖!欧拉-潘索情形终于完成了!


时间太久了,所以回顾一下该情形。
对称陀螺(拉格朗日陀螺),只受重力作用下,绕不与重心重合的固定点转动。
首先说明一下,这个情况用分析力学可以很方便求出来,但是,我刚开坑的时候没想到……,所以我就直接用\(L\)当角动量了,和拉格朗日量重了……直接用哈密顿正则方程或者哈雅方程也不是不行,但一是没必要,而是这些也应该放到前面前置知识的内容了……最重要的是,这是我学习理论力学的过程中推的,当时就用的牛顿力学,上一个情形虽然发现之前推导有问题但是小改一下就行了,这个直接大改可能要换本笔记本,懒得换了……综上,以下就使用牛顿力学的方法推导拉格朗日-泊松情形定点转动了。
200字以内,仅用于支线交流,主线讨论请采用回复功能。
自从毕业以后养成了自动跳过公式的阅读习惯,我甚至都不知道本帖应不应该加精。那么。。。就先鼓励25个K...
啊啊啊啊,太感谢了!
顺便说下这个贴还没完(我之前说一个星期内更完,打脸了)现在应该到大概六成左右,后面还有点抽象的玩意,不过下一个情形可以求解的方程的推导在书上,所以简单点,只需要求解和讨论了。
感谢建议,我去找找朋友们,也希望有些大佬可以在这科普下我不懂的椭圆函数之类的太过抽象的数学知识
200字以内,仅用于支线交流,主线讨论请采用回复功能。
我们继续拉格朗日-泊松情形的求解。由于推导到可以求解的方程的过程都在周衍柏先生的理论力学上了,所以我就简述思路再发图片,然后再求解。
思路其实不难,上文的欧拉-潘索情形,我们取了角动量方向为地面系z方向,因为此时无力矩,角动量守恒。然而,拉格朗日-泊松情形不然,由于重力的力矩,角动量在时时改变,所以我们不能这么取z方向。那么该怎么做呢?既然有重力,重力方向不变,不妨取重力的反方向为z轴正方向(emm……其实同向也行,就是看着难受)。注意到力矩和欧拉角有关,所以不能像上文一样,分开求解,必须联立6个方程……太恶心了……所以必须找点什么简化。易知这是保守系,所以能量守恒(啊啊啊啊要是我一开始就想到了拉格朗日方程求解后面就不用这么繁琐了),然后,由于重力作用在z轴方向,由于力矩是位矢和力的矢积,所以z方向力矩为零,所以z轴角动量守恒。利用这两个守恒量,我们可以大大简化求解过程。
我们不妨设\(I_1=I_2\),这和上文对称欧拉陀螺不同,不是需要满足(4.19)的原因,仅仅是习惯。
具体求解过程见下方照片和下文。


以上便是可以求解的方程的推导过程,重点注意书中的(3.9.23),(3.9.25)。
个人觉得书中的一些参量的定义不好,于是定义:
能量:\(E\)
K方向:\(\vec{e_{z}}\)
\(\vec{e_{z}}\)方向角动量(K方向角动量):\(L_z\)(即文中\(\alpha\))
仍沿用x作为章动角的余弦值(感觉字母不够了,不过这部分不会涉及到除z轴外地面系坐标,所以不会搞混,注意一下就好了)
仍沿用l作为重心到固定点距离
那么书中的(3.9.23),(3.9.25)可以被写为:
\((\dot{x})^2=\frac{2mgl}{I_1}[x^3+\frac{I_3(I_1-I_3)\omega_{30}^2-2I_1E}{2mglI_1}x^2+\frac{I_3\omega_{30}L_z-mglI_1}{mglI_1}x+\frac{I_1(2E-I_3\omega_{30}^2)-L_z^2}{2mglI_1}]\)(5.1)
\(\dot{\varphi}=\frac{L_z-I_3\omega_{30}x}{I_1(1-x^2)},\dot{\psi} = \omega_{30}-\frac{L_z-I_3\omega_{30}x}{I_1(1-x^2)}x\)(5.2)
乍看下来,都很恶心,但是好消息是我们可以通过(5.1)独立求解章动角,再代入(5.2)进行积分。
(5.1)看上去困难……实际上也困难……不过它是个常系数的三次方程,所以我们若知道确切的数据,代入得出数值解是很容易的,解析解嘛,无脑代入三次方程求根公式也是可以做到的,不过很繁琐,也和物理无关,所以下文就把解直接设出来了。所以,真正对物理重要的,是知道有几个解,它们的范围是什么。
200字以内,仅用于支线交流,主线讨论请采用回复功能。
说件事,我本人是物竞生,现在是出来上课,然后今天下午刚讲完刚体。我发现之前我独自推导的拉格朗日泊松情形的解析解其实只是一种情况。这种情形实际上有很多种情况,而且讨论特别复杂,我之前太低估了
,我原先计划今晚更完第五节的,然而应该没办法做到了,再加上明天起有事,所以可能要更得慢点。当然,我发现这比我想象的还要有意思,后面的内容会更有趣的。
对了更正一点,前文说只有三种情况可解,不过今天上课老师说有十种左右,但是除了本文谈及的两个以外几乎没有实际意义。
200字以内,仅用于支线交流,主线讨论请采用回复功能。
对函数(5.1),其实写法有很多种,后面讨论是肯定不会用这种的,不过这样看着舒服,现在就这么写吧。
我们定义:
\(f(x)=\frac{2mgl}{I_1}[x^3+\frac{I_3(I_1-I_3)\omega_{30}^2-2I_1E}{2mglI_1}x^2+\frac{I_3\omega_{30}L_z-mglI_1}{mglI_1}x+\frac{I_1(2E-I_3\omega_{30}^2)-L_z^2}{2mglI_1}]\)(5.3)
则\(\dot{x}^2 = f(x)\)
我们先来研究下f(x)的性质。
首先,由于这个问题是可解的,所以,f(x)在[-1,1]上有至少一个值大于零,因为x是章动角的余弦值,而它对时间的导数一定存在。
接下来,带进两个特殊值,计算。
有:
\(f(1)=\frac{-I_3^2\omega_{30}^2+2I_3\omega_{30}L_z-L_z^2}{I_1^2}=-(\frac{I_3\omega_{30}-L_z}{I_1})^2 \le 0\)(5.4)
\(f(-1)=\frac{-I_3^2\omega_{30}^2-2I_3\omega_{30}L_z-L_z^2}{I_1^2}=-(\frac{I_3\omega_{30}+L_z}{I_1})^2 \le 0\)(5.5)
所以,\(f(-1)<f(1)\le0\)(5.6)
所以,我们可以知道f(x)的大致形状,分为4类。
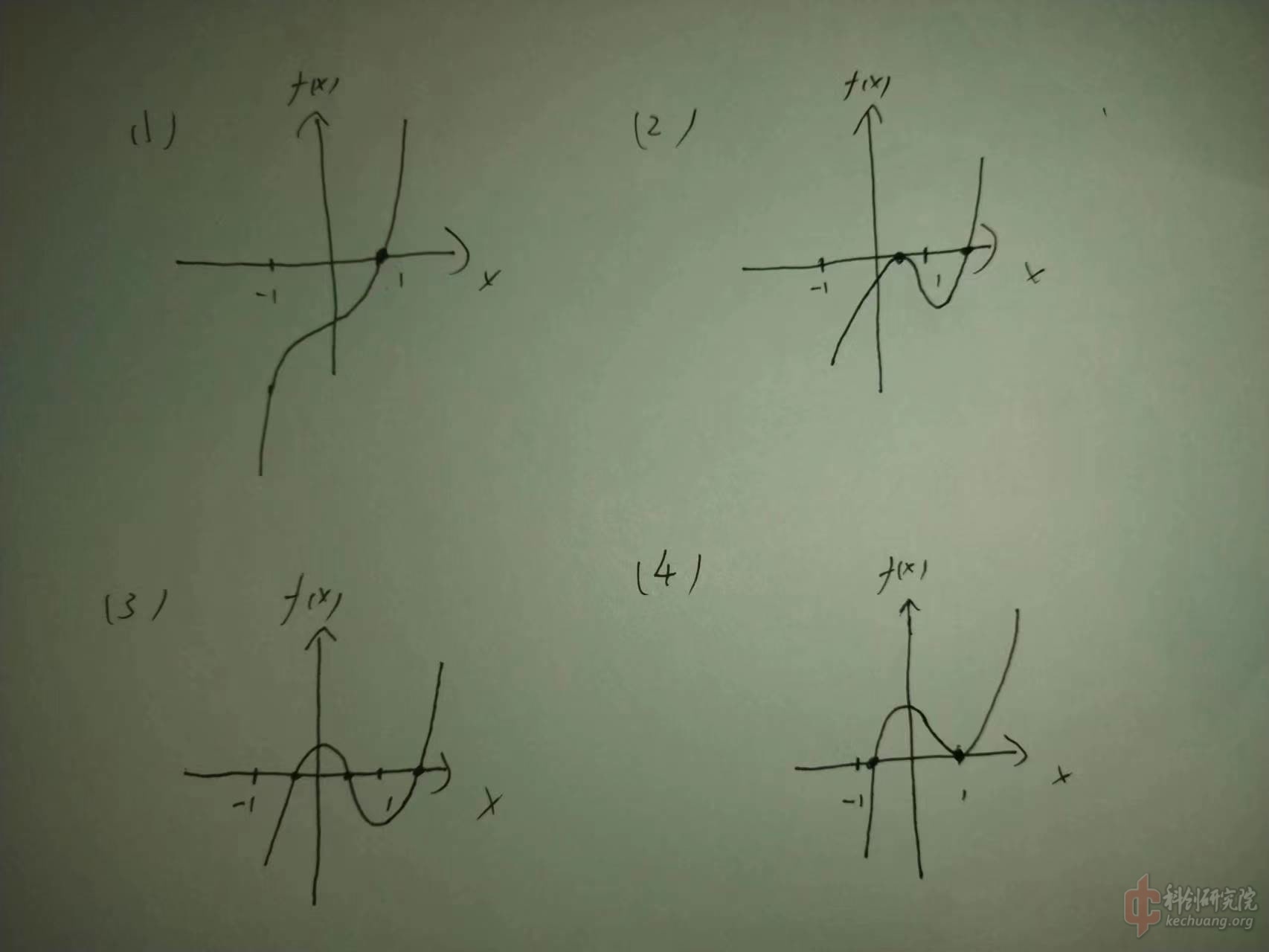
这个不方便画图,所以只能手画了。
除了情况(1),其他的包括重根都可以看作有三个零点,两个在-1到1之间,一个在1以上。
那么我们先讨论最特殊的情况(1)
此时,若要\(\dot{x}=\frac{d cos(\theta)}{dt}\)存在,只有可能\(cos(\theta)=1\),即
\(\theta=0\)(5.7)
此时章动角只可能为零。
此时由(5.2),代入可得进动角速度,自转角速度。
代入x=1,发现进动角速度是个0/0未定式,可以洛必达求解,当然最简单的方法就是取零,毕竟还是因为欧拉角的缺陷,所以按习惯取有自转无进动。也就是说,此时刚体直立旋转。不妨取初始自转角为零,有:
\(\varphi = 0,\theta = 0,\psi = \omega_{30}t\)(5.8)
200字以内,仅用于支线交流,主线讨论请采用回复功能。
十分抱歉,这几天有事,没更……我们继续。
由于f(x)除上述情况外可以看作有3个实根,不妨设:
\(f(x) = \frac{2mgl}{I_1}(x-x_1)(x-x_2)(x-x_3)\)(5.9)
由上文,我们知道这些实根的范围
不妨设\(x_1\ge 1\ge x_2\ge x\ge x_3\ge -1\)(5.10)
那么,由(5.3):
\(\dot{x}=n\sqrt{\frac{mgl}{2I_1}}\sqrt{4(x-x_1)(x-x_2)(x-x_3)}\)(5.11)
这里提出来一个4是为了后面好换元。
这个n的值是\(\pm1\),用处同前。
这里说一下,对一般的拉格朗日陀螺,实际问题中只需要代入数值求解三个根即可,理论计算中,设出来就行,这几个根可以用三次方程求根公式求解,但是本身f(x)的系数就够复杂了,再带进三次方程中……反正我是不想这么做。不过保留这三个根对实际问题没有任何影响,只是多了一步求解罢了。
接下来,对(5.11)分离变量:
\(\frac{dx}{\sqrt{4(x-x_1)(x-x_2)(x-x_3)}}=n\sqrt{\frac{mgl}{2I_1}}dt\)(5.12)
两边定积分:
\(\int_{x(0)}^{x(t)}\frac{dx}{\sqrt{4(x-x_1)(x-x_2)(x-x_3)}}=n\sqrt{\frac{mgl}{2I_1}}t\)(5.13)
对上式左端的积分,理论力学上说,可以化成椭圆积分,然而,它并没有说如何做。然后,我去查了特殊函数概论这本“字典”,找到了类似情况的换元方法。我尝试使用,然而第一次发现积分变量的取值范围不对,故自己换了一次元,然后又发现k的取值范围不对,然后又换了一次元……而且每次都是快写到最后的时候才发现,真的折磨。不过最后试出来了如何换元,以下就不一一说明之前的过程了,直接给出换元的方法。(我去,我那个时候才知道有些书上巧妙的方法到底是怎么来的,不一定是什么灵光一闪,很可能是推导出来的人用头发献祭的……)
我们换元,令\(\xi = \sqrt{\frac{x-x_3}{x_2-x_3}}\)(1145.14)
显然\(\xi\in[-1,1]\)
代入(5.13)得(这一步就直接写结果了啊,就是硬算没啥物理含义):
\(\int_{\sqrt{\frac{x(0)-x_3}{x_2-x_3}}}^{\sqrt{\frac{x(t)-x_3}{x_2-x_3}}}\frac{d\xi}{\sqrt{(1-\xi^2)(1-(\sqrt{\frac{x_2-x_3}{x_1-x_3}})^2\xi^2)}}=n\sqrt{\frac{(x_2-x_3)mgl}{2I_1}}t\)(5.15)
由定义,显然\(\sqrt{\frac{x_2-x_3}{x_1-x_3}}\in[0,1]\)
那么,(5.15)可以直接积分,然后把(5.14)代入:
\(F(arcsin(\sqrt{\frac{x(t)-x_3}{x_2-x_3}}),\sqrt{\frac{x_2-x_3}{x_1-x_3}})-F(arcsin(\sqrt{\frac{x(0)-x_3}{x_2-x_3}}),\sqrt{\frac{x_2-x_3}{x_1-x_3}})=n\sqrt{\frac{(x_2-x_3)mgl}{2I_1}}t\)(5.16)
那么,便很容易解出x(t):
\(cos(\theta) = x(t) = (x_2-x_3)sn^2(n\sqrt{\frac{(x_2-x_3)mgl}{2I_1}}t+F(arcsin(\sqrt{\frac{x(0)-x_3}{x_2-x_3}}),\sqrt{\frac{x_2-x_3}{x_1-x_3}}),\sqrt{\frac{x_2-x_3}{x_1-x_3}})+x_3\)(5.17)
在进一步设元化简之前,我们需要讨论一下这个n。
从f(x)的图像可以看出,横坐标为x,纵坐标为f(x)的点在图像上函数值大于零,且在[-1,1]之间的部分运动,所以遇到函数值为零的点,或者横坐标为-1,1的点,n的值必须改变,以改变点运动的方向。由上文的图片可以看出,三实根情况下,一定不会遇到横坐标为-1的点,而若遇到横坐标为1的点,一定同时遇到函数值为零的点。也就是说,n在f(x)=0处改变符号,即n在
\(cos(\theta)=x_3\)或\(cos(\theta)=x_2\)处改变符号。由(5.17)易知,当sn2=0时\(cos(\theta)=x_3\),当sn2=1时\(cos(\theta)=x_2\)。那么,同上文21楼的讨论,n是否改变符号对函数知无影响,所以可以当作常量取初始值。
接下来,为了方便,同上文一样定下参量(这里就和从上文取一样的了,反正是不同情况,不会搞混,反而可以一一对应,更加美观)
\(\lambda = n\sqrt{\frac{(x_2-x_3)mgl}{2I_1}}\)(5.18)
\(\mu = F(arcsin(\sqrt{\frac{x(0)-x_3}{x_2-x_3}}),\sqrt{\frac{x_2-x_3}{x_1-x_3}}) = F(arcsin(\sqrt{\frac{cos(\theta_0)-x_3}{x_2-x_3}}),\sqrt{\frac{x_2-x_3}{x_1-x_3}})\)(5.19)
\(k = \sqrt{\frac{x_2-x_3}{x_1-x_3}}\)(5.20)
那么,(5.17)便可以化成:
\(cos(\theta)=(x_2-x_3)sn^2(\lambda t+\mu,k)+x_3\)(5.21)
这样,结合(5.2)便可以得出拉格朗日-泊松情况在f(x)有三个实根情况下的一般解。
200字以内,仅用于支线交流,主线讨论请采用回复功能。
那么我们可以得出拉格朗日-泊松情况的一般解:
当\(f(x)\)仅一实根\(x_1=1\)(5.22.a.0)时:
\(\varphi = 0\)(5.22.a.1)
\(\theta = 0\)(5.22.a.2)
\(\psi = \omega_{30}t\)(5.22.a.3)
当\(f(x)\)有三实根\(x_1\ge 1\ge x_2\ge x_3\ge -1\)(5.22.b.0)时:
\(\varphi = \int_0^t\frac{L_z-I_3\omega_{30}[(x_2-x_3)sn^2(\lambda t+\mu,k)+x_3]}{I_1(1-[(x_2-x_3)sn^2(\lambda t+\mu,k)+x_3]^2)}dt+\varphi_0-2a_\varphi\pi\)(5.22.b.1)
其中\(a_\varphi\)为使得\(\varphi\in[0,2\pi]\)的自然数。
\(\theta = arccos[(x_2-x_3)sn^2(\lambda t+\mu,k)+x_3]\)(5.22.b.2)
\(\psi = \omega_{30}t-\int_0^t\frac{L_z-I_3\omega_{30}[(x_2-x_3)sn^2(\lambda t+\mu,k)+x_3]}{I_1(1-[(x_2-x_3)sn^2(\lambda t+\mu,k)+x_3]^2)}[(x_2-x_3)sn^2(\lambda t+\mu,k)+x_3]dt+\psi_0-2a_\psi\pi\)(5.22.b.3)
其中\(a_\psi\)为使得\(\psi\in[0,2\pi]\)的自然数。
好了,(5.22)便是拉格朗日-泊松情况的一般解。然而第五部分还未结束,因为要讨论。对此种情况,像上文一样讨论初始角速度集中在某轴上而后会发生什么变化,来寻找稳定情况是没有意义的,因为存在力矩,角动量时时改变。所以,接下来要讨论的是1.无章动时(即规则进动),进动如何2.有章动时的定性分析3.快速自转陀螺以及陀螺形状(即1、3轴转动惯量大小关系)对运动有何影响4.直立旋转陀螺的稳定性。
200字以内,仅用于支线交流,主线讨论请采用回复功能。
接下来,我们开始讨论第一点,即无章动情况下的拉格朗日-泊松陀螺的转动。
首先,既然要无章动,那x必须仅有一个取值。即上文1、2情形。
对(1),其运动方程便是(5.8),所以这里着重讨论(2)。
代入(5.22)我们可以很容易地得出运动方程,不过由于有根直接设处,无法得出条件,所以我们直接从f(x)出发。
为了方便,我们设几个参量:
\(\alpha = \frac{2E-I_3\omega_{30}^2}{I_1}\)(5.23)
\(\beta = \frac{2mgl}{I_1}\)(5.24)
\(a = \frac{I_3\omega_{30}}{I_1}\)(5.25)
\(b = \frac{L_z}{I_1}\)(5.26)
将以上四式,代入31楼图中的f(x)
有:\(f(x) = (1-x^2)(\alpha-\beta x)-(b-ax)^2\)(5.27)
这样的形式固然不好看,但是在以下的讨论中很有用。
那么(5.2)可以写成:\(\dot{\varphi}=\frac{b-ax}{1-x^2},\dot{\psi}=\omega_{30}-\frac{b-ax}{1-x^2}x\)(5.28)
那么,我们可以开始讨论(2)情形了。
此时,我们可以明显发现,x为f(x)的二重根,那么,由定义,有:
\(f(x) = (1-x^2)(\alpha-\beta x)-(b-ax)^2=0\)(5.29)
\(\frac{df(x)}{dx} = 3\beta x^2+2(\alpha+a^2)x+2ab-\beta=0\)(5.30)
回顾下(5.23)-(5.26),发现\(\beta,a\)是较容易测量的。而\(\alpha,b\)虽然也为常量,但是较难测量,所以我们打算尝试换掉它们。
由(5.29):\(\frac{\alpha-\beta x}{1-x^2}=(\frac{b-ax}{1-x^2})^2 = \dot{\varphi}^2\)(5.31)
将(5.31)代入(5.30),以消去\(\alpha,b\),得到:
\(2x\dot{\varphi}^2-2a\dot{\varphi}+\beta =0\)(5.32)
以上便是无章动情况下进动角速度应得满足的条件。
值得说明的是,在舒幼生先生的力学第五章中,也有该式的推导,不过该书式普通物理学,所以没讲得太深,而且和本文的符号不同,所以就不引用了,不过也有很大参考价值。
很容易看出,(5.32)是关于进动角速度的二次方程,其有解的条件便是判别式大于等于零,即:
\(4a^2-8x\beta\ge 0\)(5.33)
代入各参量的值,条件可化为\(cos(\theta)\le\frac{I_3^2\omega_{30}^2}{4mglI_1}\)(5.34)
发现当\(\theta>\frac{\pi}{2}\)时,一定成立。
而\(\theta>\frac{\pi}{2}\)时,需满足:\(\omega_{30}\ge\frac{2\sqrt{mglI_1cos(\theta)}}{I_3}\)(5.35)
那么,我们可以解出:
\(\dot{\varphi}=\frac{a\pm\sqrt{a^2-2\beta x}}{2x}=\frac{I_3\omega_{30}\pm\sqrt{I_3^2\omega_{30}^2-4mglI_1cos(\theta)}}{2I_1cos(\theta)}\)(5.36)
欸等等,如果\(\theta=\frac{\pi}{2}\),即x=0怎么办?要么(5.36)洛必达取极限(注意此时只能取-,这样才是0/0未定式,取+就是正无穷,显然物理世界中不存在,因为这样能量就是正无穷),要么直接从(5.32)推,有:
\(\dot{\varphi}=\frac{mgl}{I_3\omega_{30}}\)(5.37)
我比较喜欢用洛必达推的那种方法,因为这样可以看作(5.36)仍然成立。
现在,我们只能得到必要条件,那么这是否充分呢?
这时我们就得回到一般运动规律了。
现在(5.21)两边都对时间求导,有:
\(\dot{x}=(x_2-x_3)\frac{d}{dt}(sn^2(\lambda t+\mu,k))\)(5.38)
显然重根情况x2=x3,即上式为零,章动角不变。
这就证明了充分性。
现在我们总结下第一点讨论,若f(x)满足(1),那么运动规律便是(5.8),若f(x)满足(2),那么运动规律:
\(\varphi=\frac{I_3\omega_{30}\pm\sqrt{I_3^2\omega_{30}^2-4mglI_1cos(\theta_0)}}{2I_1cos(\theta_0)}t+\varphi_0-2a_\varphi\pi\)(5.39.1)
其中\(a_\varphi\)为使得\(\varphi\in[0,2\pi]\)的自然数。
\(\theta = \theta_0\)(5.39.2)
\(\psi = \frac{(2I_1-I_3)\omega_{30}\mp\sqrt{I_3^2\omega_{30}^2-4mglI_1cos(\theta_0)}}{2I_1}t+\psi_0-2a_\psi\pi\)(5.39.3)
其中\(a_\psi\)为使得\(\psi\in[0,2\pi]\)的自然数。
(5.39)即是无章动情况下的运动方程。
如何理解呢?(5.39)的意思是,若要满足无章动的条件,那么必须在满足(5.34)的3轴角速度条件前提下,满足(5.39.1)的进动条件,这时,便无章动且自转情况为(5.39.3)。好比手中有一个静止的理想陀螺仪,我希望维持在某个章动角稳定进动,那么我必须先根据(5.34)计算出应该满足的三轴角速度,拉绳子或者用电机啊之类的什么把陀螺仪的3轴角速度,也就是此时的自转角速度,陀螺转速(现在相当于手拿着还没进动),提升到(5.34)的条件,然后再用手推一下,使得初始进动角速度满足(5.39.1),那么接下来它便会稳定进动了。
给个视频链接,没找到保存后还能动的动图……
这可能是规则进动,不过为什么是“可能”?后面会说,埋个伏笔。
为了简化计算或者定性分析的难度,我们还要做些近似工作,为与实际情况接轨,此时着重考虑进动角速度,其余的实际上不重要,需要用也可以直接代(5.2)。
由(5.36),我们可以知道,对同一个章动角,无章动且3轴角速度满足条件时,满足规则进动的有一大一小两个进动角速度。
先看小的:
如果进动角速度很小,那么它的平方可以略去,即(5.32)近似为:
\(-2a\dot{\varphi}+\beta=0\)(5.40)
则:\(\dot{\varphi}=\frac{\beta}{2a}=\frac{mgl}{I_3\omega_{30}}\)(5.41)
再看大的:
如果进动角速度很大,那么(5.32)中常数项可以略去,近似为:
\(x\dot{\varphi}-a =0\)(5.42)
则:\(\dot{\varphi} =\frac{a}{x}=\frac{I_3\omega_{30}}{I_1cos(\theta)}\)(5.43)
不难发现,上述讨论都在3轴角速度很大的时候近似得很好,所以这启发我们研究快速自转的陀螺。当然,虽然现在还不知道快速自转的陀螺怎样,但已经知道在自转角速度很大时可以用以上近似。除此之外,在章动角很接近\(\frac{\pi}{2}\)时可以用(5.43)的近似,但是在章动角等于\(\frac{\pi}{2}\)时不行,此时这个近似和精确解一样会趋于无穷大,此时只有一个进动角速度满足条件,即(5.37)
200字以内,仅用于支线交流,主线讨论请采用回复功能。
接下来我们看看有章动的情况下的定性分析。
就像欧拉-潘索情况下有潘索描绘,可以让我们直观地想象刚体的运动,拉格朗日-泊松情形也需要一种图像表示方式。
我们重点关注进动角速度的方向。
由(5.28)或(5.2),我们可以发现,当章动角逐渐变小到某个锐角,即章动角的余弦值逐渐变大到某一个正值时,我们可以发现进动角速度逐渐变小,变为零,然后反向,变大,直到章动角到达最小值后章动角速度反向,进动角速度也变减小,变为零,然后反向到与原先同向。
如果上述情况可以达成,那么进动角速度为零的临界章动角\(\theta_c\),由(5.2)有:
\(\theta_c = arccos(\frac{L_z}{I_3\omega_{30}})\)(5.44)
那么记x2、x3对应的角度为\(\theta_2\)、\(\theta_3\)
那么我们可以分类:
\(\theta_c>\theta_3>\theta_2\)(a)
\(\theta_3=\theta_c>\theta_2\)(b)
\(\theta_3>\theta_c>\theta_2\)(c)
\(\theta_3>\theta_c=\theta_2\)(d)
\(\theta_3>\theta_2>\theta_c\)(e)
我们现在关注自转轴在以固定点为球心的球面上划出的轨迹。
这个也不好用电脑画,只能再次用手了

抱歉各位,只能再看我的渣画了。
不妨设\(\theta>\theta_c\)时,进动逆时针,反之,顺时针。
那么有图像:
(实线表示\(\theta_2\)、\(\theta_3\)所对应的等章动角线,虚线表示\(\theta_c\)所对应的等章动角线,带箭头的实线即表示自转轴再以固定点为球心的球面上划出的轨迹)

欸等等,这里b,d情况是不是有点不对劲?为啥会出现突变,不是说不能突变吗?实际上这里并没有什么问题,此时进动角速度为零,那么轨迹的斜率,章动加速度比进动角速度当然不存在。
实际上,d反而是最常见的情况,接近直立的陀螺倒下来便是如此。这也解释了为什么陀螺不会倾倒。很多科普视频上说,重力给了个力矩,所以角动量沿着重力的力矩方向改变,而重力的力矩无z轴的分量,所以角动量的方向旋转改变,大小不变陀螺便不会倾倒。然而这是错的,如果陀螺倾倒,角动量某个分量大小增加,也满足。所以,这种解释仅适用于规则进动的情况。有章动的情况,定量计算就是拉格朗日-泊松情形的一般规律(5.22)。而定性解释,可以用上图理解。舒幼生先生的力学中给出了一个非常好的定性说明。如果进动角速度太小,那么由角动量的旋转所带来的角动量变化,将小于重力的力矩导致的变化,于是陀螺将会向下章动,形成重力力矩方向的角动量。而此时,由上文的讨论,进动角速度也同时增加,角动量矢量旋转导致的变化逐渐变得等于、大于重力的力矩导致的变化,于是陀螺开始减小向下章动的角速度,逐渐转而向上章动。这不仅解释了陀螺为何会倾倒,也解释了章动的产生。
200字以内,仅用于支线交流,主线讨论请采用回复功能。
接下来,我们讨论一下快速自转陀螺,即:
\(\frac{1}{2}I_3\omega_{30}^2>>mgl\)(5.45)
此时,自转太快以至于进动章动等重力引起的效应都可以认为是微扰。
那么初始时进动角速度就应当为零,由(5.28):
\(b=ax(0)\)(5.46)
又由于能量由转动动能和重力势能组成:
\(E = \frac{1}{2}I_3\omega_{30}^2+mglx(0)\)(5.47)
代入(5.23)(5.24),有:
\(\alpha=\beta x(0)\)(5.48)
代入f(x),有:
\(f(x)=(x(0)-x(t))[(1-x^2(t))\beta-a^2(x(0)-x(t))]\)(5.49)
换元:\(X = x(0)-x(t)\)(5.50)
那么:
\(f(X)=\beta X(X^2+(\frac{a^2}{\beta}-2x(0))X+x^2(0)-1)\)(5.51)
显然,\(X_0=0\)为该函数一零点。
而\(\frac{a^2}{\beta}=\frac{I_3^2\omega_{30}^2}{2I_1mgl}\)(5.52)
由(5.45)可知,除非极其细长的陀螺使得\(I_3<<I_1\),一般情况下\(\frac{a^2}{\beta}>>1\)。
那么,\(-2x(0)\)可以略去,而前面说了进动章动看作微扰,所以X2可以略去。
那么较小的一个零点满足\(\frac{a^2}{\beta}X+x^2(0)-1=0\)(5.53)
解得,\(X_1=\frac{\beta}{a^2}sin^2(\theta_0)=\frac{2I_1mgl}{I_3^2\omega_{30}^2}sin^2(\theta_0)\)(5.54)
那么\(\Delta x = x_0 - x_1 = X_1 - X_0 = \frac{2I_1mgl}{I_3^2\omega_{30}^2}sin^2(\theta_0)\)(5.55)
由上式和(5.45)可以看出\(\Delta x <<1\),即章动的幅度很小。
接下来,我们想求解章动和进动的具体运动方程。
由于章动幅度很小,可以做近似\(1-u^2(t)\approx 1-u^2(0)=sin^2(\theta_0)\)
代入(5.49)可知:\(\dot{X}=\dot{x}=f(x)=a^2X(X_1-X)=-a^2(X-\frac{X_1}{2})^2+a^2\frac{X_1^2}{4}\)(5.56)
上式左右两次求导,同时消去两侧一阶导数项,利用\(\ddot{X}=\ddot{(X-\frac{X_1}{2})}\)有:
\(\ddot{(X-\frac{X_1}{2})}+a^2(X-\frac{X_1}{2})=0\)(5.57)
这个方程我们很熟悉,常系数齐次二阶微分方程,简谐振动中常常出现,解得:
\(X=Acos(at+\phi)+\frac{X_1}{2}\)(5.58)
由上可知\(\Delta x\)为两倍的振幅,即\(A=\frac{\Delta x}{2}=\frac{X_1}{2}\)(5.59)
代入t=0:\(\frac{X_1}{2}(1+cos(\phi))=0\),即\(\phi =\pi\)(5.60)
代入积分常数后,我们便得到:\(X=\frac{X_1}{2}(1-cos(at))\)(5.61)
将(5.50)代入(5.61),再将各参量代入利用反余弦函数得到:
\(x=cos(\theta) = \frac{mglI_1}{I_3^2\omega_{30}^2}sin^2(\theta_0)(1-cos(\frac{I_3\omega_{30}}{I_1}t))+cos(\theta_0)\)(5.62)
(5.62)式显示出来章动角仅再初始章动角附近摆动,且3轴角速度越大,章动越小,对高速自转陀螺,章动甚微。
将(5.62)、(5.46)代入(5.2)第一式:
\(\dot{\varphi}= \frac{a(x(0)-x(t))}{sin^2(\theta_0)}=\frac{aX}{sin^2(\theta_0)}=\frac{mgl}{I_3\omega_{30}}(1-cos(\frac{I_3\omega_{30}}{I_1}t))\)(5.63)
(5.63)对时间取平均即得:
\(\bar{\dot{\varphi}}=\frac{mgl}{I_3\omega_{30}}\)(5.64)
由上面两式可见,此时陀螺以变化的进动角速度缓慢进动,而且此时平均进动角速度与上文讨论的规则进动中缓慢进动角速度一致。
代入(5.2)第2式,由于进动角速度远远小于3轴角速度,所以可近似为:
\(\dot{\psi}=\omega_{30}\)(5.65)
那么,积分,便可以得出此时的运动方程:
\(\varphi = \frac{mgl}{I_3\omega_{30}}(t-\frac{I_1}{I_3\omega_{30}}sin(\frac{I_3\omega_{30}}{I_1}t))+\varphi_0-2a_\varphi\pi\)(5.66.1)
其中\(a_\varphi\)为使得\(\varphi\in[0,2\pi]\)的自然数。
\(\theta = arccos( \frac{mglI_1}{I_3^2\omega_{30}^2}sin^2(\theta_0)(1-cos(\frac{I_3\omega_{30}}{I_1}t))+cos(\theta_0))\)(5.66.2)
\(\psi = \omega_{30}t+\psi_0-2a_\psi\pi\)(5.66.3)
其中\(a_\psi\)为使得\(\psi\in[0,2\pi]\)的自然数。
如果我们再取一次近似,那么:
\(\varphi = \frac{mgl}{I_3\omega_{30}}t+\varphi_0-2a_\varphi\pi\)(5.67.1)
其中\(a_\varphi\)为使得\(\varphi\in[0,2\pi]\)的自然数。
\(\theta = \theta_0\)(5.67.2)
\(\psi = \omega_{30}t+\psi_0-2a_\psi\pi\)(5.67.3)
其中\(a_\psi\)为使得\(\psi\in[0,2\pi]\)的自然数。
(实际上(5.66)已经是从近似中推出的,现在(5.67)则是为了进一步简化继续近似)
也就是说,这个时候,看上去,陀螺似乎是以(5.67)的形式,匀速进动,无章动,匀速自转地定点转动,然而实际上不是,而是(5.66)形式,略微有章动,且以缓慢变化的小角速度进动。实际上,陀螺由于阻力等原因,几乎无法观测到章动。这样,我们称之为赝规则进动。
这也说明了陀螺的形状对其的影响,一般我们买到的陀螺玩具都是扁平的,因为不需要过高的转速就可使(5.52)远远大于1,使陀螺进入赝规则进动状态。
(我去,我写这里的时候被查水表了,因为我去年搜索了ap的制作方法……不过所幸无大事)
200字以内,仅用于支线交流,主线讨论请采用回复功能。
接下来,我们讨论下直立转动陀螺的稳定性
初始时无章动且章动角为零:\(\theta = 0,\dot{\theta}=0,x(0)=1\)(5.68)
此时由于欧拉角的缺陷,无法分清进动和自转,同样地,取进动角和进动角速度为零。
\(\varphi = 0,\dot{\varphi}=0\)(5.69)
仿照(5.46)(5.48)的推导方法,我们有:
\(a=b\)(5.70)
\(\alpha =\beta\)(5.71)
那么,代入f(x),有:\(f(x)=(1-x^2)(\beta (1+x)-a^2)\)(5.72)
易知,此时\(x =1\)为一重根,\(x = \frac{a^2}{\beta}-1\)为一单根。
此时仍然可以看作在重根处稳定进动,由(5.33)式,\(\frac{a^2}{\beta}-1>1\),不能取值。
所以,容易看出\(x = 1\)为对章动角的平衡位置。接下来我们讨论平衡的稳定性。
现在在t = 0时施加一微扰:\(\dot{\theta} = \varepsilon\)(5.73)
注意了,这个时候相当于不考虑f(x)仅一实根的特殊情况了,因为你给出一个微扰,就破坏了这种特殊情况,所以就可以看作三实根的情况。
依然仿照(5.46)(5.48)的推导方法,利用定义,我们有:
\(a=b,\alpha =\beta +\varepsilon^2\)(5.74)
代入f(x),有:\(f(x) = -(1-x)(\beta x^2-(a^2+\varepsilon^2)x+a^2-\beta-\varepsilon)\)(5.75)
这时一次多项式与二次多项式乘积的形式,我们可以解出三个零点:
\(1\)(5.76.1)
\(\frac{a^2+\varepsilon^2-\sqrt{(a^2-2\beta+\varepsilon^2)^2+8\beta\varepsilon^2}}{2\beta}\)(5.76.2)
\(\frac{a^2+\varepsilon^2+\sqrt{(a^2-2\beta+\varepsilon^2)^2+8\beta\varepsilon^2}}{2\beta}\)(5.76.3)
当判别式\(\Delta\)为有限值时,即\(a^2\ne2\beta\)时,泰勒展开,近似到二阶小量,三个零点为:
\(1\)(5.77.1)
\(1-\frac{2\varepsilon^2}{a^2-2\beta}\)(5.77.2)
\(1+\frac{a^2-2\beta}{\beta}+\frac{a^2\varepsilon^2}{\beta(a^2-2\beta)}\)(5.77.3)
当判别式\(\Delta\)为小量时,即\(a^2=2\beta\)时,泰勒展开,近似到一阶小量即可,三个零点为:
\(1\)(5.78.1)
\(1-\sqrt{\frac{2}{\beta}}\varepsilon\)(5.78.2)
\(1+\sqrt{\frac{2}{\beta}}\varepsilon\)(5.78.3)
我们发现不论如何三个零点定有一个大于1,一个等于1,一个小于1,对应着前文的x1、x2、x3,即此时:\(x_1>x_2=1>x_3\)
那么结合(5.22.b.2),发现章动幅度为\(x_2-x_3\),这个情况中,x2=1,此时章动幅度为:
\(1-x_3\)(5.79)
那么接下来的事情就是讨论不同情况下上式是否仍然为一个小量:
当\(a^2>2\beta\)时,x3取(5.77.2):\(1-x_3 = \frac{2\varepsilon^2}{a^2-2\beta}\)(5.80)
仍为一小量。
当\(a^2=2\beta\)时,x3取(5.78.2):\(1-x_3 = \sqrt{\frac{2}{\beta}}\varepsilon\)(5.81)
仍为一小量。
当\(a^2>2\beta\)时,x3取(5.77.3):\(1-x_3 = \frac{2\beta-a^2}{\beta}+\frac{a^2\varepsilon^2}{\beta(2\beta-a^2)}\)(5.82)
此时振幅是一个有限值!
综上,直立陀螺的稳定条件便是:\(a^2\ge2\beta\),即:
\(\omega_{30}\ge\frac{2\sqrt{2mglI_1}}{I_3}\)(5.83)
临界3轴角速度即是:
\(\omega_c=\frac{2\sqrt{2mglI_1}}{I_3}\)(5.83)
现实中,稳定直立旋转的陀螺,将会因为摩擦力矩等等原因使得3轴角速度降低,降到临界角速度时,便不再稳定。
高速自转陀螺,由定义,一定满足这种情况,称为睡陀螺,也是会在降低到临界角速度后不再稳定。
200字以内,仅用于支线交流,主线讨论请采用回复功能。
芜湖!第五部分完成!看样子本文终于接近尾声了。
第六部分是简要讨论下刚体的一般运动,毕竟只是简要讨论,我就大概说下思路,本部分无公式。
由于刚体的一般运动可以分解为一个点的平动和绕该点定点转动,我们不妨取质心,这样就可以转化为质心参考系简化后面的运算了。
取质心为参考点有一个很好的作用,由于换系后很可能是非惯性系,所以要加一个惯性力,而惯性力作用于质心,所以在质心参考系中,质心是固定点,平动惯性力无力矩,所以不用考虑,当然如果是转动惯性力那就基本上没辙了……电脑仿真吧。
但是虽然仅在平动非惯性系下可解依然有很重要等等作用。
列举一些。
1.(近似)无重力情况下刚体运动,不用说了,符合欧拉潘索情形。
2.刚体抛掷,近地面情况下,重心与质心重合,此时质心系中无力矩!求解质心运动,然后用欧拉潘索情况求解刚体绕质心运动即可!
3.短时间内包括空气阻力对快速移动物体姿态的影响,换质心系,短时间内空气阻力大小可以看作恒定,若压心与质心重合,则可视为欧拉潘索情形,若不重合,则可视为拉格朗日泊松情形。
200字以内,仅用于支线交流,主线讨论请采用回复功能。
好了,这应该是本文最后一个部分了,讨论下本文所述的内容有什么实际意义。
首先,假设你是僧正,你正在开开心心地调戏上条当麻和御坂美琴,没想到右方之火不知好歹尽然打断你的好戏,于是你随手把他打成陀螺。这个时候,你如果不去追上条当麻和御坂美琴,那么你就会看到(忽略空气阻力)——右方之火的质心在做斜抛运动,而他本人在绕质心做欧拉潘索定点转动

上述告诉我们欧拉潘索运动可以用于求解忽略空气阻力下刚体投掷问题

好吧不开玩笑了,我大概说些可能能用的地方。
1.火箭航电,这个我不了解,之前试过去做,结果飘得很厉害,我觉得本文可能有助于调超参数那一块……
2.电磁炮弹丸的稳定性,本文提供的理论应该可以计算弹丸如果使用转动增稳需要多大转速之类的问题,我最近似乎没空,以后有空了算一下,可行的话发上来
emm……我似乎想不到更多的用处了
那么……
完结洒小花

200字以内,仅用于支线交流,主线讨论请采用回复功能。
追加一个部分。说下原因,本人参加了一个数学建模大赛,其中用了本文部分内容作为模型。写那个论文的时候需要画图,买不起matlab,自己用python写了一个,就是画欧拉潘索情形的。自我感觉还不错,就发上来分享一下。偷懒就没写图形化窗口了,以后有时间可能会写,或者把它包装成库什么的。其他就不多说了,上源码。
import numpy as np
from matplotlib import pyplot as plt
from scipy import special,integrate
import random
#调整字体
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def omega_t(t):
#这里序号不一样!是定义的原因
w1 = A[0]*special.ellipj(a*t+b,k*k)[1]
w2 = A[1]*special.ellipj(a*t+b,k*k)[0]
w3 = A[2]*special.ellipj(a*t+b,k*k)[2]
return w1,w2,w3
def e3_ta(t):
return np.sqrt((I[0]**2)*(omega_t(t)[0]**2)+(I[1]**2)*(omega_t(t)[1]**2))/((I[1])*(omega_t(t)[1]))
def e3_tb(t):
return (I[0])*(omega_t(t)[0])/np.sqrt((I[0]**2)*(omega_t(t)[0]**2)+(I[1]**2)*(omega_t(t)[1]**2))
def e3_t(t):
df_dt = (e3_tb(t+lim[3]/2)-e3_tb(t-lim[3]/2))/lim[3]
return e3_ta(t)*df_dt
def e1_t(t):
return L*(omega_t(t)[2]-e3_t(t))/(I[2]*omega_t(t)[2])
def eular_t(t):
e2 = np.arccos(I[2]*omega_t(t)[2]/L)
e3 = integrate.quad(e3_t,a=0,b=t)[0]+eular0[2]
e1 = integrate.quad(e1_t,a=0,b=t)[0]+eular0[0]
return e1,e2,e3
print('欢迎使用刚体自由定点转动(欧拉潘索情形)绘图器\n制作者为辰星引力航天工作室\n本绘图器将得出三主轴角速度及以角动量方向为极轴的欧拉角\n本绘图器得出欧拉角不含使得欧拉角处在定义域中的常数')
#初始化上、下限、作图步长、精确度、微扰
lim = [0,0,0,0,0]
while True:
c = input('请输入时间上下限,作图步长,积分求导精确度,微扰。格式:t0,t,d1,d2,d3')
d = c.split(',')
if not len(d) == 5:
print('请输入正确的格式')
continue
try:
for i in range(5):
lim[i] = float(d[i])
except:
print('请输入正确的格式')
continue
if lim[2] <= 0:
print('作图步长必须大于零')
continue
if lim[3] <= 0:
print('积分求导精确度必须大于零')
continue
if lim[4] == 0:
print('微扰不可等于零')
continue
break
#初始化主轴惯量
I = [0,0,0]
#初始化三轴角速度
omega0 = [0,0,0]
#初始化欧拉角
eular0 = [0,0,0]
while True:
c = input('请输入三个主轴惯量,和对应的初始角速度,初始欧拉角(章动角θ与初始角度无关,只是为了形式整齐,随便填个数就行)。格式:I1,I2,I3;O1,O2,O3;φ,θ,ψ')
d = c.split(';')
try:
for i in range(len(d[0].split(','))):
I[i]=float((d[0].split(','))[i])
for i in range(len(d[1].split(','))):
omega0[i]=float((d[1].split(','))[i])
for i in range(len(d[2].split(','))):
eular0[i]=float((d[2].split(','))[i])
except:
print('请输入正确的格式')
continue
if len(I)==3 and len(omega0) == 3 and len(eular0) == 3:
for i in I:
if i <= 0:
print('主轴惯量应大于零')
continue
break
print('请输入正确的格式')
#排序
if I[0]>I[1]:
tr1 = I[0]
I[0] = I[1]
I[1] = tr1
tr2 = omega0[0]
omega0[0] = omega0[1]
omega0[1] = tr2
if I[1]>I[2]:
tr1 = I[1]
I[1] = I[2]
I[2] = tr1
tr2 = omega0[1]
omega0[1] = omega0[2]
omega0[2] = tr2
if I[0]>I[1]:
tr1 = I[0]
I[0] = I[1]
I[1] = tr1
tr2 = omega0[0]
omega0[0] = omega0[1]
omega0[1] = tr2
#不想讨论了,直接加个小量防止出现除零错误
if I[1] == I[2]:
I[2]+=lim[3]
#这里加微扰是为了模拟真实情况
for i in range(3):
omega0[i] += lim[4]
#初始化动能和角动量平方
T = 0
L2 = 0
for i in range(3):
T+=0.5*I[i]*(omega0[i]**2)
L2+=(I[i]**2)*(omega0[i]**2)
L = np.sqrt(L2)
if (I[2]-I[1])*(L2-2*I[0]*T)<(I[1]-I[0])*(2*I[2]*T-L2):
tr1 = I[2]
I[2] = I[0]
I[0] = tr1
tr2 = omega0[2]
omega0[2] = omega0[0]
omega0[0] = tr2
#函数形如Ae(a*t+b,k)/e()为某个椭圆函数
k = np.sqrt(((I[1]-I[0])*(2*I[2]*T-L2))/((I[2]-I[1])*(L2-2*I[0]*T)))
a = np.sign(omega0[2])*np.sign(I[2]-I[0])*np.sqrt((I[2]-I[1])*(L2-2*I[0]*T)/(I[0]*I[1]*I[2]))
b = special.ellipkinc(np.arcsin(np.sqrt(I[1]*(I[2]-I[1])/(2*I[2]*T-L2))*omega0[1]),k*k)
A = []
A.append(np.sqrt((2*I[2]*T-L2)/(I[0]*(I[2]-I[0]))))
A.append(np.sqrt((2*I[2]*T-L2)/(I[1]*(I[2]-I[1]))))
A.append(np.sign(omega0[2])*np.sqrt((L2-2*I[0]*T)/(I[2]*(I[2]-I[0]))))
time = np.arange(lim[0],lim[1],lim[2])
omega = [[],[],[]]
omega = omega_t(time)
eular = [[],[],[]]
for i in time:
for j in range(3):
eular[j].append(eular_t(i)[j])
ti1='一般刚体自由定点转动三轴角速度随变化时间关系'
ti2='一般刚体自由定点转动欧拉角随时间变化关系'
#初始化画布对象,并调整窗口
fig = plt.figure(figsize=(12, 5), dpi=100)
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)
#绘制三轴角速度随时间变化
ax1.set_title(ti1)
ax1.plot(time,omega[0])
ax1.plot(time,omega[1])
ax1.plot(time,omega[2])
ax1.set_xlabel('t')
ax1.set_ylabel('三轴角速度')
ax1.legend(['1轴角速度','2轴角速度','3轴角速度'])
ax1.axhline(0)
ax1.axvline(0)
#绘制欧拉角随时间变化
ax2.set_title(ti2)
ax2.plot(time,eular[0])
ax2.plot(time,eular[1])
ax2.plot(time,eular[2])
ax2.set_xlabel('t')
ax2.set_ylabel('欧拉角')
ax2.legend(['进动角','章动角','自转角'])
ax2.axhline(0)
ax2.axvline(0)
fig.savefig('刚体自由定点转动')
plt.show()本程序为了体现变化情况,就舍去了欧拉角的定义域,还有,为了不讨论那么多分母会趋于零的极限,索性加个小量,不过呢,这样反而更好地看出微扰,而且由于直接加小量,章动角不可能严格为零,所以章动角很小的时候不会默认把进动算作自转。
放个效果图,记得之前说的网球拍定理吗?
这是只有1轴方向有角速度,其他方向是微扰(为了明显起见,微扰设得很大)的情况:

这是只有2轴方向有角速度,其他方向是微扰(为了明显起见,微扰设得很大)的情况:

这可以验证网球拍定理。
对了,说下,这个自用的,没考虑什么代码的效率,算起来很慢

如果有发现程序出问题的,可以跟我说,不过我最近有些事,可能没法很快回……不过看看是不是库少了之类的先。

200字以内,仅用于支线交流,主线讨论请采用回复功能。