对函数（5.1），其实写法有很多种，后面讨论是肯定不会用这种的，不过这样看着舒服，现在就这么写吧。

我们定义：

$f(x)=\frac{2mgl}{I_1}[x^3+\frac{I_3(I_1-I_3){\omega }_{30}^2-2I_{1}E}{2mgl{I}_1}{x}^2+\frac{I_3{\omega }_{30}{L}_z-mgl{I}_1}{mgl{I}_1}x+\frac{I_1(2E-I_3{\omega }_{30}^2)-L_z^2}{2mgl{I}_1}]$(5.3)

则${\dot{x}}^2=f(x)$

我们先来研究下f(x)的性质。

首先，由于这个问题是可解的，所以，f(x)在[-1,1]上有至少一个值大于零，因为x是章动角的余弦值，而它对时间的导数一定存在。

接下来，带进两个特殊值，计算。

有：

$f(1)=\frac{-I_3^2{\omega }_{30}^2+2I_3{\omega }_{30}{L}_z-L_z^2}{I_1^2}=-(\frac{I_3{\omega }_{30}-L_z}{I_1}{)}^2\le 0$(5.4)

$f(-1)=\frac{-I_3^2{\omega }_{30}^2-2I_3{\omega }_{30}{L}_z-L_z^2}{I_1^2}=-(\frac{I_3{\omega }_{30}+L_z}{I_1}{)}^2\le 0$(5.5)

所以，$f(-1)<f(1)\le 0$(5.6)

所以，我们可以知道f(x)的大致形状，分为4类。

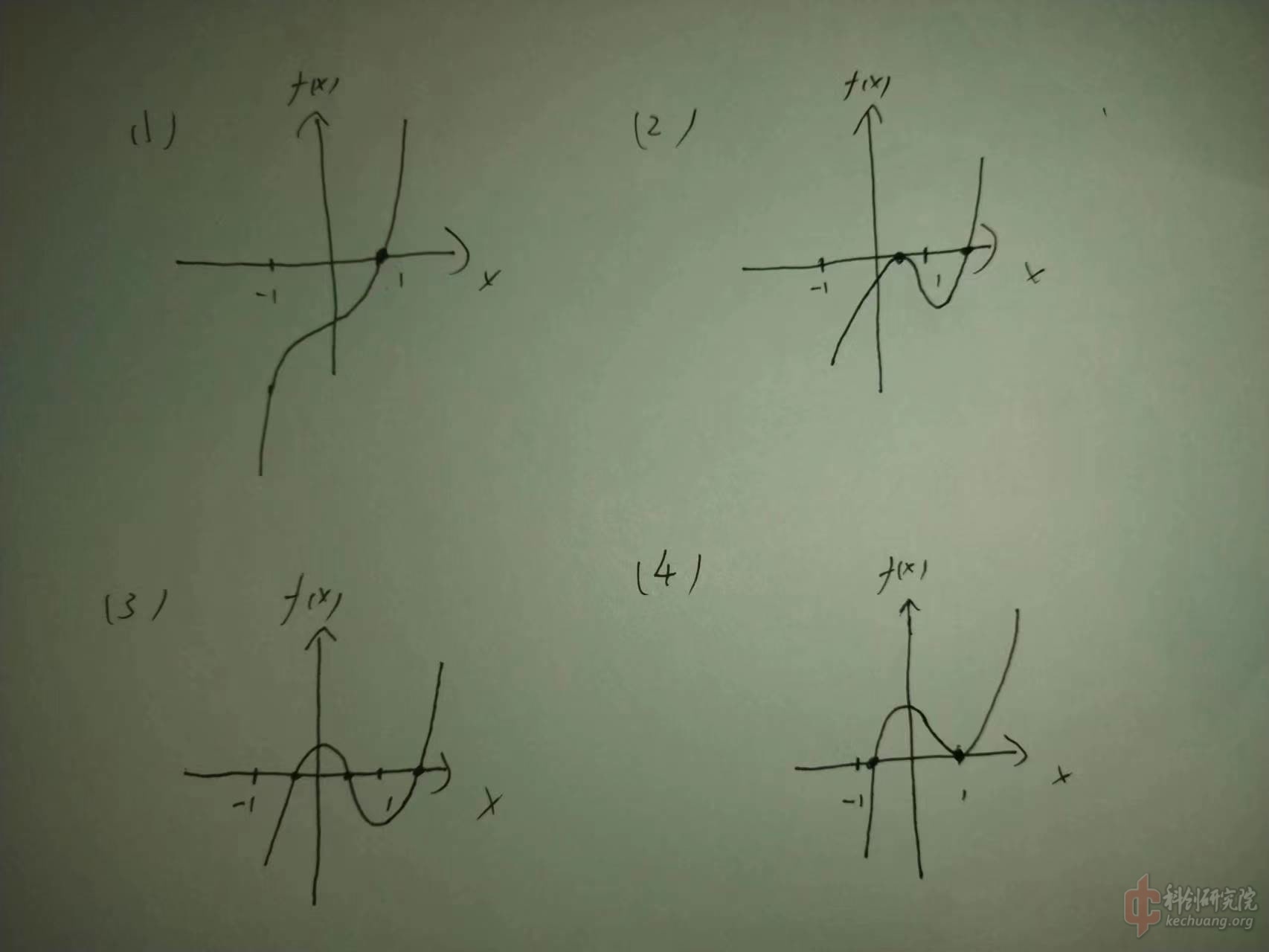
这个不方便画图，所以只能手画了。

除了情况（1），其他的包括重根都可以看作有三个零点，两个在-1到1之间，一个在1以上。

那么我们先讨论最特殊的情况（1）

此时，若要$\dot{x}=\frac{dcos(\theta )}{dt}$存在，只有可能$cos(\theta )=1$，即

$\theta =0$(5.7)

此时章动角只可能为零。

此时由（5.2），代入可得进动角速度，自转角速度。

代入x=1，发现进动角速度是个0/0未定式，可以洛必达求解，当然最简单的方法就是取零，毕竟还是因为欧拉角的缺陷，所以按习惯取有自转无进动。也就是说，此时刚体直立旋转。不妨取初始自转角为零，有：

$\phi =0,\theta =0,\psi ={\omega }_{30}t$(5.8)