4.勒让德第一类椭圆积分和一些雅氏椭圆函数的定义：

对\(\int_{0}^{u}\frac{d\xi}{\sqrt{(1-\xi^2)(1-k^2\xi^2)}}\)(1.7)的积分：

若有\(u\in[-1,1]\)和\(k\in[0,1]\)

我们可以换元，令\(\xi = sin(\alpha),u = sin(\phi)\)

即有\(\int_{0}^{\phi}\frac{d\alpha}{\sqrt{1-k^2sin^2(\alpha)}},\phi=arcsin(u)\in[-\frac{\pi}{2},\frac{\pi}{2}]\)(1.8)

这个积分无法用有限的基本初等函数表示，我们将这个积分的结果记作\(F(\phi,k)\)或\(F(arcsin(u),k)\)

可以求得它的级数表示：

\(F(\phi,k)=\phi+\sum_{n = 1}^{\infty}(\frac{(2n-1)!!}{(2n)!!}\int_{0}^{\phi}(ksin(\alpha))^{2n}d\alpha)\)(1.9)

特别地，如果\(\phi = \frac{\pi}{2}\)即\(u=1\)，这时(1.9)中求和号内的积分可以积出，此时称为勒让德第一类完全椭圆积分，记作\(K(k)\)，有\(K(k) = F(\frac{\pi}{2},k) = \frac{\pi}{2}(1+\sum_{n = 1}^{\infty}(\frac{(2n-1)!!}{(2n)!!}k^n)^2)\)(1.10)

注意上面的!!并不是取完阶乘后再取一次，而是重阶乘，我第一次遇到的时候也以为是取两次，因为卡西欧是这么算的

这个很重要，不知道这个定义看不懂啊！！！(注意！这里的“！！！”不是三重阶乘，只是感叹号，包括本句句首的“！”也只是感叹号)

从上面似乎可以看出\(F(\phi,k)\)的定义域是\([-\frac{\pi}{2},\frac{\pi}{2}]\),但我们总可以使用被积函数的偶函数和周期函数特性，将其定义域延拓至整个实数集，我们有：

\(\int_{0}^{\phi+2c\pi}\frac{d\alpha}{\sqrt{1-k^2sin^2(\alpha)}}=\int_{0}^{\phi}\frac{d\alpha}{\sqrt{1-k^2sin^2(\alpha)}}+4c\int_{0}^{\frac{\pi}{2}}\frac{d\alpha}{\sqrt{1-k^2sin^2(\alpha)}},\phi\in[-\frac{\pi}{2},\frac{\pi}{2}],c\in Z\)

即\(F(\phi+2c\pi,k) = F(\phi,k)+4cK(k),\phi\in[-\frac{\pi}{2},\frac{\pi}{2}],c\in Z\)

不妨设\(k = \frac{114514}{191981}\) ,作图即可直观地看到被积函数的性质：

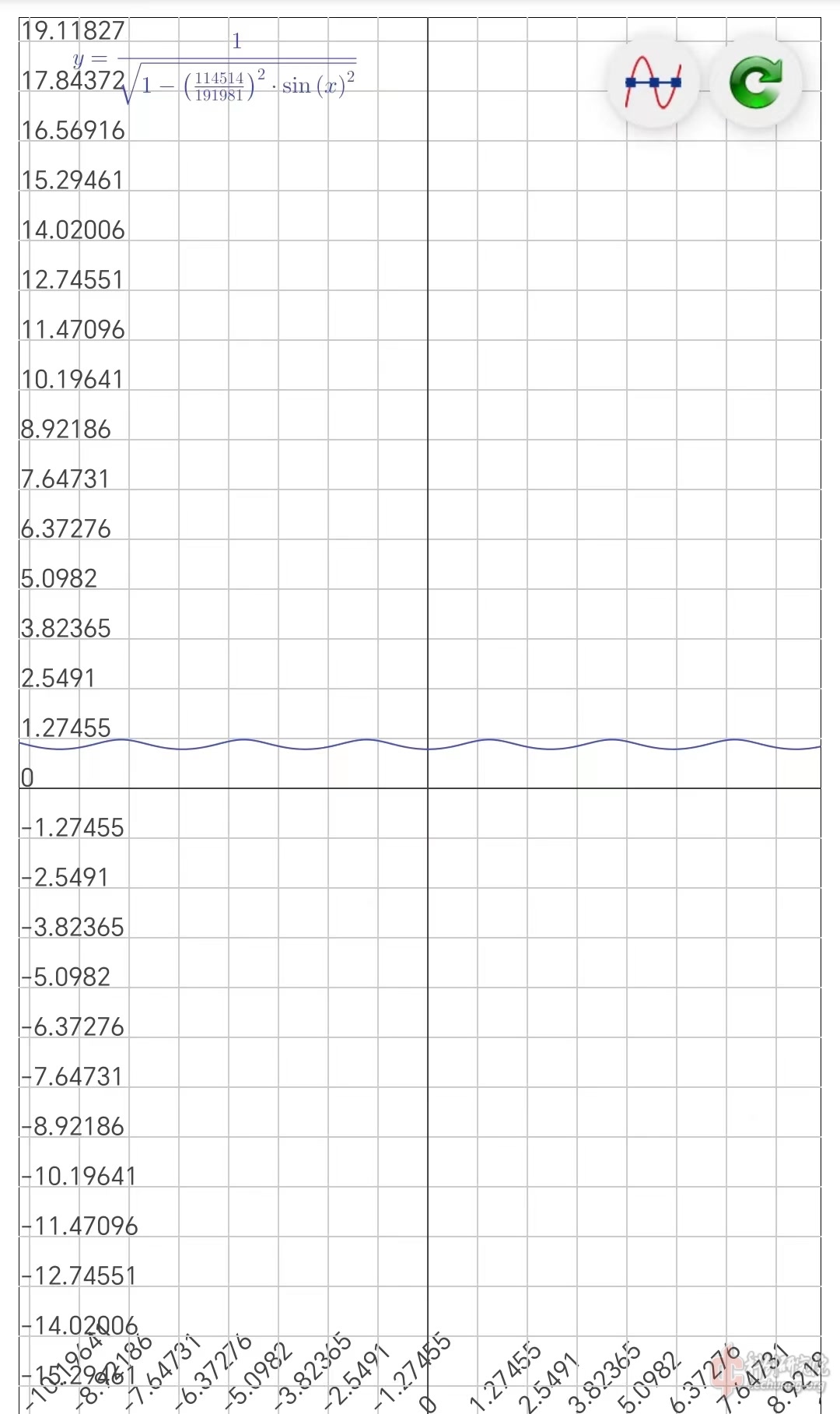
注意！积分(1.7)时仍要确保\(u\in[-1,1]\)

如果我们把k看作参量，可以得到它的反函数，记作\(am(\beta,k)\)

有\(\beta = F(\phi,k),\phi = am(\beta,k)\)(1.11)

定义函数：

\(sn(\beta,k)=sin(am(\beta,k))\)(1.12)

\(cn(\beta,k)=cos(am(\beta,k))\)(1.13)

\(dn(\beta,k) = \sqrt{1-k^2sn^2(\beta,k)}\)(1.14514)

椭圆函数作为数学的一个重要分支，肯定不止这些，我也是在学习理论力学的过程中发现需要用到临时学的，也仅仅刚好够用于求解刚体定点转动，有大佬懂的话还请科普

前置知识点就这些了，一会给出在哪里可以系统学习。

对了，给论坛提一下建议，就是这个公式编辑器能不能做到更加人性化一点呢？就这点我输了一个半小时（好像还有个鼠标移到上面公式编辑器那个按钮会乱蹦的bug……）