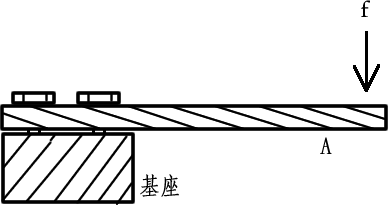
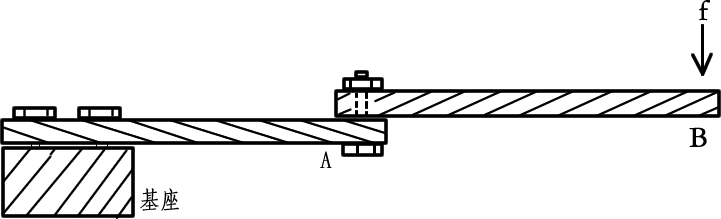
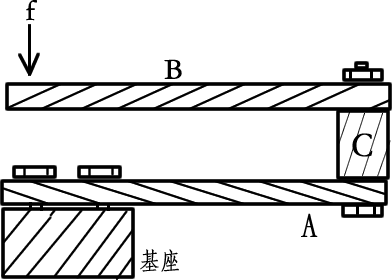
引用 虎哥:提到的磁平衡天平,是另一种结构,其支撑秤盘的悬臂其实并未移动。
这个传感器真的怪异,不论物体放在盘子上的什么位置,结果相同。
就是梅特勒的磁平衡天平,大体上仍然满足此规律。。
称,是诞生了几千年的东西。说起来不应该有多么复杂的原理,为啥咱就理解不了呢。。
挖个坟,看前面讨论太热烈了,忍不住
这个两板重叠面积对结果有重大影响,处理不好实验很容易不好,对于第二种情况可以用两种切变模量差距较大的材料头对头焊起来,感觉比较好。
我觉得第二种情况还有种算法:
根据剪切形变的胡克定律公式:F/S=G△d/△D
变形:△d=(F/GS)△D ……①
对于第二种情况,可以当做一个变模量的物体处理,即:
G= {G₁ ,0<=D<L
{→+ οο ,L<=D<2L (即刚体,1/G=0)
对①积分:d= { (F/G₁S)D ,0<=D<L
{ (F/G₁S)L ,L<=D<2L
D=L时,d=(F/G₁S)D,这与直接令G=G₁算出来的情况一相同
更关键的来了,我在想情况三的时候看到了106楼,“感觉好像一耳光被抽醒”
他在分析情况三时使用了一种重要思想——等效,但是不彻底,让我来发扬光大这种思想:
对于情况二三,只要外部受力不变,可以改变作用的方法,换句话说,你不用关心是用手压还是用桌子压,如106楼所说“情况3可以考虑为U型弹簧在U的两个末端受压”。
既然可以这样,那么情况二三就不用关心哪头是受桌子的力,哪头是人为压力。情况就可以等效为,刚性板固定在桌子上,给弹性板施加压力 然后既然固定在桌子上的板是刚性的,那么可以继续等效为弹性板直接固定在桌子上
然后既然固定在桌子上的板是刚性的,那么可以继续等效为弹性板直接固定在桌子上
 小学生也能看出3者形变相同,问题蜕变为小学问题。
小学生也能看出3者形变相同,问题蜕变为小学问题。
PS:如果不等效这不可能是初中问题,切变模量这东西高中奥赛都不大学,大一才学。不过这题可以作为初中物理奥赛题,考点是等效的思想而不是计算和公式
还有电子称不是因为使用了桥式电路而前后左右移动不影响读数吗?
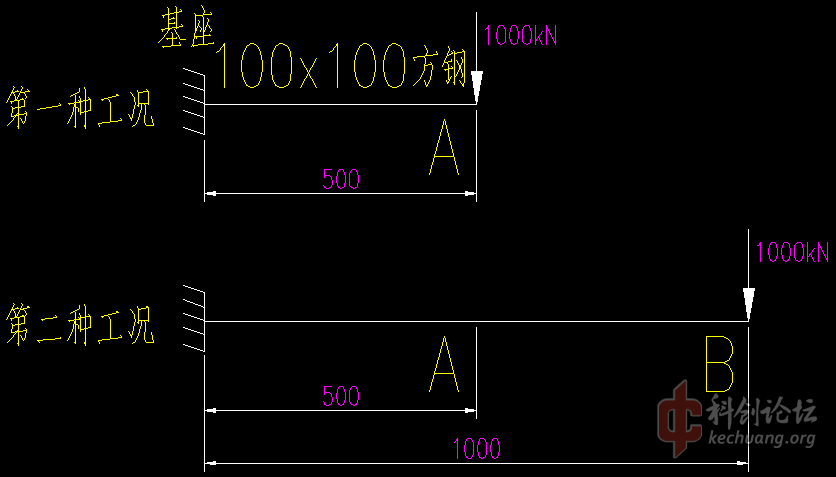
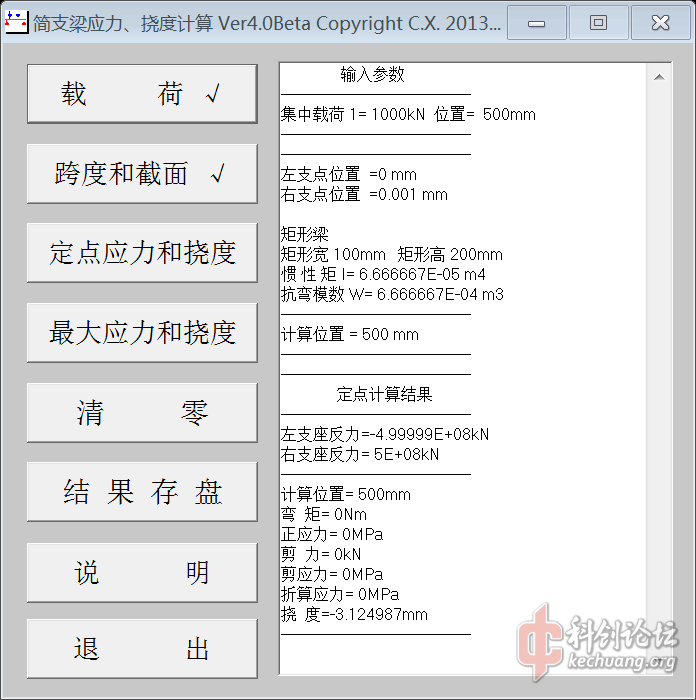
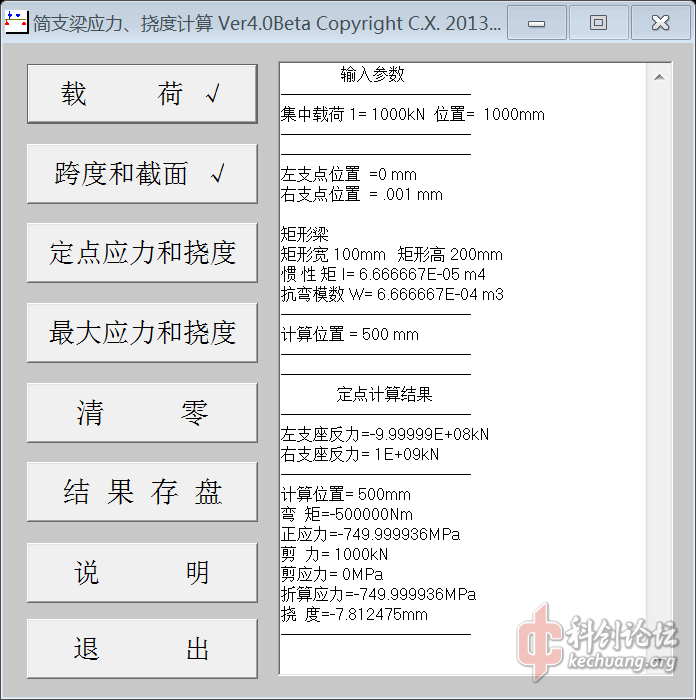
首先这不是一道初中题,这是一道材料力学题,大一水平吧。我用软件计算得出的结论是2.5倍。
我用软件计算得出的结论是2.5倍。
我看到您是改变了右支点的位置,但是此题中其中一段是刚性梁,我看您的计算没有体现到。(不过根据我的计算这个不影响情况2)
您计算的挠度是是支点处的吧,情况2问的只是第一根弹性梁端点处的下降
这样的题考初中生,可以说算是有些超纲了,至少要了解理论力学以及材料力学中的一些内容才能求解,而这些都是大学才涉及到的。
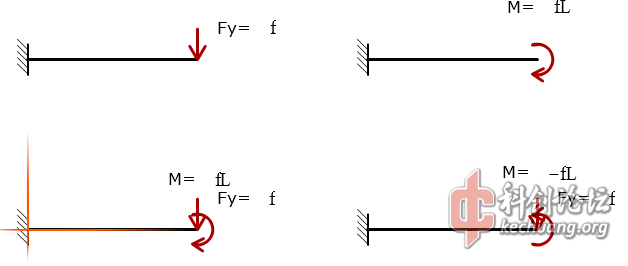
第一幅图,自由端位移为
第二幅图,
第三幅图中,仍然使用刚体中力系等效原理,等价为
应该要考虑C 的尺寸啊!如果C的尺寸占了杆子的一半呢?那很明显了吧!
第二个问题中,弹性片是S型形变。这个肯定不是中学能解决的问题,只能用有限元去模拟。
第二个问题中B杆是刚性的,如果B杆是弹性的,才会是S形变(如下图,中间为螺栓连接。灰色曲线为变形后的曲线)。对于后者,也不需要用有限元模拟,用材料力学挠曲线方程求解超静定问题即可。

完全理想化是可以大概计算的。杆弹性系数连续,其他物件参数理想,可以根据杠杆原理计算力矩。
这个问题初中无解,高中也不行,大学《工程力学》可以。把力和弯矩化到a点,分别查资料,得到挠度,再把挠度相加就是最终变形。
如果这是初中物理的话,
认真分析一下题目:
1.基座和施力点并没有严格说明作理想化(实际对结果会有不小的影响);
2.附加的杆是轻质,刚性,则暗示了这是理想化后的;
3.附加杆的长度也是迷惑人的,因为施力点同样没有严格表述。
综上,这个题目放在初中是考力产生的形变,因为施加的力大小一样,所以形变也会一样。
但这个题目实际上并不严谨,实际真实情况是施加力的方向和作用点都会影响弹性杆的形变,所以实验不能完美复现形变一致这个完美答案。
都是2mm
第一题,b杆右端受到力f,而b杆静止,合力矩是零,所以左端与a杆对b杆的作用力大小也是f,但方向相反。根据力的相互作用得,b杆对a杆右端的力也是f,方向向下,所以结果与给出的例子相同,是2mm。
用第一题的方法第二题也很容易求得。
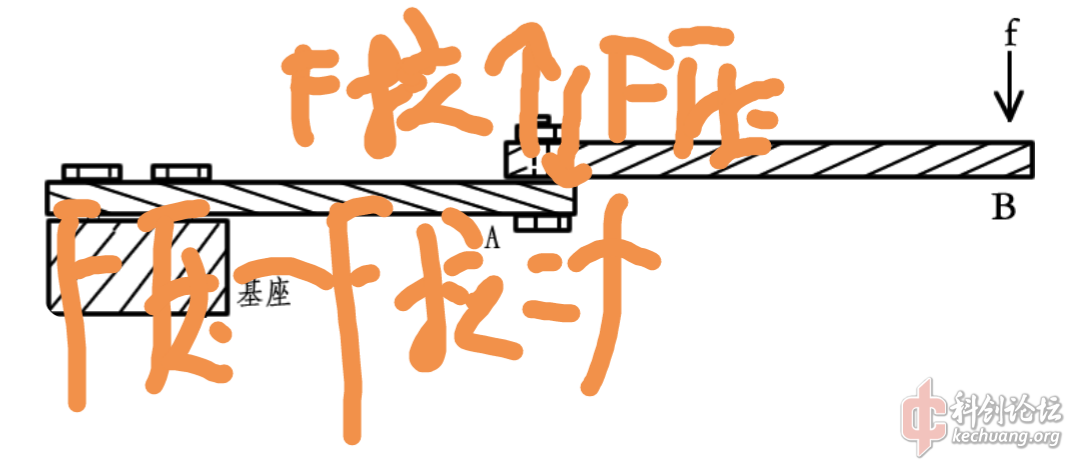
等效于在A点用力f压
第三个同理
所以都是2mm
也可以直接把上面部分看作一个整体,反正力又不会凭空多出来
不知是否正确,感觉这个题可以用初中的整体思想方法,像是高中提前招生类的题
我看到您是改变了右支点的位置,但是此题中其中一段是刚性梁,我看您的计算没有体现到。(不过根据我的计算...
搞不清楚大家把这个简单的材料力学问题搞得如此复杂,居然动用了有限元和模拟模型,该翻翻材料力学的书了。我在帖子里用的软件是我自己编写的,在上至三峡,下至向家坝,经过很多次工程的大型启闭机实践计算证明是正确的。仔细看看我软件计算的两个支点位置,我是用两个靠得很近的支点来模拟悬臂梁,懂点材料力学的人应该明白吧。是这种小问题根本用不着有限元,我也是个搞了钢结构20多年的高工,象ansys、Autodesk Simulation Mechanical、Nastran也常用,不是不会,是没必要。
计算简图





200字以内,仅用于支线交流,主线讨论请采用回复功能。