在这个频率有太多不同构型的天线可以使用了,没有太明白一定要用平板反射器的意义?
可以考虑一下MOXON, 八木之类的天线,方便制作且效果很好
我在射频方面是个新手 无奈为LORA设备买到的便宜天线 都比较磕碜 看中的定向平板天线总觉得太贵 于是打算自制 当然是可能失败的 毕竟网上也找不到平板定向天线的资料 只能自己想象了
目标是
极化方面: 应该是线极化 垂直极化
尺寸应该不超过70mm (因为这个尺寸覆铜板便宜好买)
能做到大致某个方向的定向 但是要求不高
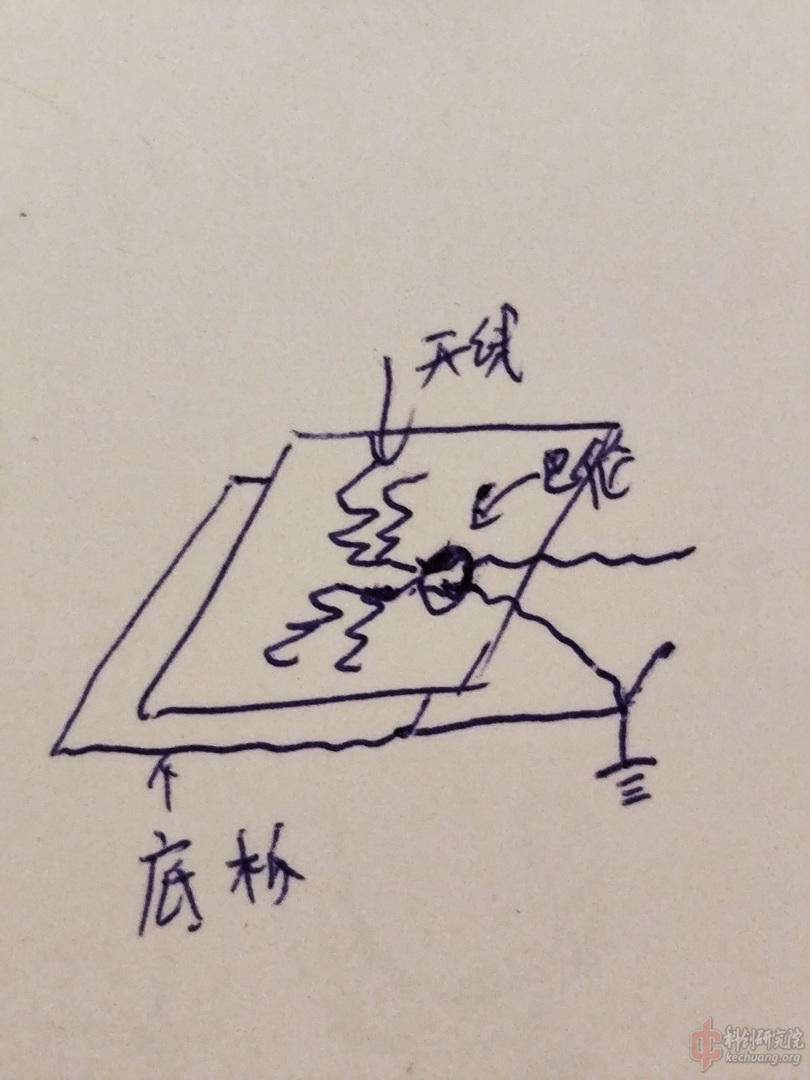
预期的结构是这样的:
单面覆铜板上构造出天线 偶振子类型 垂直极化 使用2根不同长度分支来对433/470MHz频段进行覆盖 蛇形走位来减少占用尺寸
另一块平行的金属板 可能是铝板或者覆铜板 与前者构成波导 使得辐射只朝一个方向 之所以不在一块双面覆铜板上实现两者 是因为这样波导阻抗太低 天线效率可能会降低太多 后期匹配也不方便
预期的步骤是这样的:
购买单面覆铜板 测试其参数 包括厚度和介电系数 (因为买的是电木的 所以介电系数不清楚)
使用微带线计算器 按两板间隔20mm 计算缩短系数 然后根据1/4波长 设计振子长度 并留有余量
制作覆铜板 安装
用VNA测试阻抗 调整两板间距 找一个合适匹配的阻抗
用VNA测试谐振频率 并通过截短甚至手动延长振子的方式 调整成想要的频率点和覆盖带宽
最后用巴伦进行阻抗匹配和完成平衡变换
目前已买尺寸70mm左右的覆铜板 尚未到货 在kicad上模拟了一下 使用1.5mm线宽是个尺寸不错的选择 可以轻松画下2对分支
因为没有射频经验 也不知道这样中不中 只能试试
在这个频率有太多不同构型的天线可以使用了,没有太明白一定要用平板反射器的意义?
可以考虑一下MOXON, 八木之类的天线,方便制作且效果很好
在这个频率有太多不同构型的天线可以使用了,没有太明白一定要用平板反射器的意义?可以考虑一下MOXON...
这不是平板反射器
moxon我看了一下 感觉并不完美 八木更复杂且庞大
而且我的目的 并不是为了很窄的定向 而是具备足够的覆盖范围
这不是平板反射器moxon我看了一下 感觉并不完美 八木更复杂且庞大而且我的目的 并不是为了很窄的定...
我习惯性的将这种大一点平面叫做反射器了。。。MOXON也不是很窄,方向图比较稳定。不太明白你的用途,可以大概讲解一下嘛?
LORA随便一个鞭状天线就可以搞几公里,还需要设计天线么?
我习惯性的将这种大一点平面叫做反射器了。。。MOXON也不是很窄,方向图比较稳定。不太明白你的用途,...
比方说一个农场吧 一般LORA基站面对的子站群 通常是在同一个方向 比如坐北朝南 但又不是一对一 ...
当然成品是有卖的 最便宜也不到100 一种方法是拆来研究 但是我没有在网上见到任何拆解或者研究结果 我觉得保持好奇心是很重要的 所以想科创而不仅仅满足于现有的不太合心的替代 同时也可以学习天线知识 保持学习和研究心态
如果什么都止步于 "XXX不就够了" 我觉得压根就没有吃喝拉撒之外的需求了
首先 这是一个偶振子天线与微带结构的结合
光从微带结构说 应该称为"倒置微带线" 网上有计算特征阻抗和等效介电常数的工具 在设计天线长度时候 应该相当有用

(发这个图片的时候 才发现CTRL-V就能直接上图 ... 太吓人了 幸好我没有CTRTL-C什么不合适的图)
因为好奇 我看了javascript里面的算法 追查了用的公式的来源 应该来自一本国外的书 书名"Microstrip Lines and Slotlines : Third Edition, Section 2.5.1, P110"


有出处就好 mathworks也采用了他的算法 应该可信 不过由于蛇形走位 而且有较多辐射 预期需要的天线长度应该还要更小
天线部分 网上的推导多采用微带线加耗损的模型 将总辐射功率根据天线微元上的电流分布进行分配 然后计算出输入阻抗

其中l是天线长度
k 是相位系数 从模型上认为是2π/λ
βa=R1/2Wa 是等效衰减系数, 其中R1=
而其中RΣ就非常复杂了 根据远区坡印廷矢量积分算出辐射功率 再推算出的辐射电阻 但此处有个问题 对比开放的偶振子天线 我这里是应该只有半边辐射的 RΣ就只有一半 (但是这个结论是粗糙存疑的 不知道是否有人指点一下)

Wa 是理想无耗损传输线的阻抗 这里带入网上工具算出来的 大概250Ω
根据上面模型 写个程序 可以得到天线输入阻抗与天线长度的关系图
Pythonimport scipy.integrate
import numpy
from matplotlib import pyplot
wa=250
ratio_from=0
ratio_to=0.5
ratio=numpy.linspace(ratio_from+0.001, ratio_to-0.001, 1001)
k_l=ratio*2*numpy.pi
r_sigma=numpy.array([30*scipy.integrate.quad(
lambda theta, kl: ((numpy.cos(kl*numpy.cos(theta))-numpy.cos(kl))**2)/numpy.sin(theta),
0, numpy.pi,
args=(t,)
)[0] for t in k_l])
r1_l=r_sigma*2/(1-numpy.sin(2*k_l)/(2*k_l))
beta_a_l=r1_l/2/wa
t=wa/(numpy.cosh(2*beta_a_l)-numpy.cos(2*k_l))
ra=(numpy.sinh(2*beta_a_l)-beta_a_l/k_l*numpy.sin(2*k_l))*t
xa=-(numpy.sin(2*k_l)+beta_a_l/k_l*numpy.sinh(2*beta_a_l))*t
amp=numpy.sqrt(ra*ra+xa*xa)
ang=numpy.arctan2(xa, ra)*180/numpy.pi
print('At {}λ, RΣ={}, impedance={} + {}j'.format(
0.25,
numpy.interp(0.25, ratio, r_sigma),
numpy.interp(0.25, ratio, ra),
numpy.interp(0.25, ratio, xa)))
fig, ax1=pyplot.subplots()
fig.subplots_adjust(right=0.85)
ax1.set_title('Input impedance of antenna')
ax1.set_xlabel('l/λ')
ax1.set_ylabel('Impedance (Ω)', color='blue')
ax1.set_ylim(0, 500)
ax1.set_xlim(ratio_from, ratio_to)
ax1.set_xticks(numpy.linspace(ratio_from, ratio_to, 5))
ax1.grid()
ax1.plot(ratio, amp, linewidth=1, color='blue')
ax1.plot(ratio, r_sigma, linewidth=1, color='black')
ax2=ax1.twinx()
ax2.set_ylabel('Phase (°)', color='orange')
ax2.set_ylim(-90, 90)
ax2.grid()
ax2.plot(ratio, ang, linewidth=1, color='orange')
z=numpy.complex(0, 1)*xa+ra
z0=numpy.complex(numpy.interp(0.25, ratio, ra), 0)
rf=(z-z0)/(z+z0)
vswr=(1+numpy.abs(rf))/(1-numpy.abs(rf))
fig, ax3=pyplot.subplots()
fig.subplots_adjust(right=0.85)
ax3.set_title('VSWR')
ax3.set_xlabel('l/λ')
ax3.set_ylabel('VSWR', color='black')
ax3.set_ylim(1, 3)
ax3.grid()
ax3.plot(ratio, vswr, linewidth=1, color='black')
pyplot.show()

但非常无奈的是 左右检查 仍然与网上文章的图形有出入 主要是在1/4波长上 我计算的结果是略微容性 而网上的图片会有明显的感性 (需要注意的是 下图的表达是与上图不同的 上图是幅度/角度 下图是实部/虚部)

下图应该是符合真实的 表现出因为末端放电导致的缩短系数 但是我盘算以上整个推算步骤 是没有这方面的体现的 应该是在计算之外 本来就i不该显示在结果中 只能通过经验 缩短设计1%-5% (由于印刷天线截面积小 这个效应实际应该不明显)
此外不同的是 计算范围如果是 0-λ 我的结果与上图就截然不同了 主要区别是0.75λ处我计算有个可用的天线长度

也有可能是相位系数k的问题 毕竟天线上电流分布的模型 不一定能合适用在所有天线长度上 但是并没有找到更好的模型
假定我的计算是正确的 那么可以看出 实际是1/4左右波长是辐射效率最大的 此时输入阻抗接近并略小于开放偶振子的辐射功率电阻73Ω/2(半封闭) 比3/4波长处的效率要高 在1/2波长附近 虽然有0相位点 但是阻抗比微带线的特征阻抗还高 应该没有多少辐射
看看驻波比

在当前设计下 如果需要保证驻波比小于1.5(反射系数0.2) 从图中获取数据并计算了一下 大概可以容纳6%的频带宽度 对于450MHz 有大概27MHz 感觉差不多可以覆盖437-463MHz 如果减少背板距离 增加微带线的宽度 减少微带线特征阻抗 这个带宽会变大 不过我打算使用双分支天线 这样覆盖430-435MHz就应该没有问题了 470-510MHz看情况可能真需要调整一下)
天线大抵是这样的 具体尺寸根据到货板子测量后调整

----------------------------- 6.21 ------------------
发现上面的推导有重大问题 !!!!
最大的问题是 k这个参数 没有考虑到微带线上的速度与空气中的速度区别 混用了
其次就是蛇形天线并不合适使用以上的微带计算公式 因为有转弯 带来更多的电感 有许多靠近 又没有周围的过孔屏蔽 导致新的串扰电容 结果就具有目前难以预期的滤波效果
其次就是输入阻抗的推导 首先是坡印廷矢量的积分不对 蛇形横向的电流元是相互有部分抵消的 不能算入 这样RΣ就可能比直线型的要小不少 其次是"耗损电阻平均分布在振子上"这个前提可能不对 继续用带衰减的传输线公式来计算也可能不对
真令人头疼啊 果然必须得仿真吗 或者勉强再算算
假设平行的蛇形线间仅仅相互抵消 不考虑其他相位和电/磁感应的话 这种天线可以等效为数段短天线相连 中间有固定时延 但是不妨假设电流驻波幅度在短天线间连续(并非电流波本身 而是驻波幅度) 末端电流驻波为0 这样的话
假设空气中相位系数为k0 天线上相位系数为k1 天线上电流驻波最大幅度为Im 蛇形天线真实高度为h
分段积分实在难搞 不妨假定分段够多够细够均匀(比如斜线走位) 那么

其中η0是自由空间阻抗120π
Python>>> from sympy import integrate, symbols, sin, cos
>>> k0, k1, l, h, z, j, theta=symbols('k0 k1 l h z j theta')
>>> r1=integrate(sin(k1*l*(h-z)/h)*(cos(k0*z*cos(theta))+j*sin(k0*z*cos(theta))), (z,0,h), conds='none')
>>> r2=integrate(sin(k1*l*(h+z)/h)*(cos(k0*z*cos(theta))+j*sin(k0*z*cos(theta))), (z,-h, 0), conds='none')
>>> r=(r1+r2).simplify()
>>> print(r)
2*h*k1*l*(cos(k1*l) - cos(h*k0*cos(theta)))/(h**2*k0**2*cos(theta)**2 - k1**2*l**2)仍然假设分段够多够细够均匀 耗损电阻仍然平摊 仍然采用原有的"有耗损的末端开路的传输线模型"
Python>>> import sympy
>>> from sympy import symbols
>>> from sympy import integrate
>>> from sympy import sin
>>> l,h,z,k1,r_sigma=symbols('l,h,z,k1,r_sigma')
>>> y=integrate(sin(k1*(h-z)*l/h)**2, (z,0,h), conds='none').simplify()
>>> r1=r_sigma/y*h/l
>>> r1.simplify()
4*k1*r_sigma/(2*k1*l - sin(2*k1*l))......
按我上面设计 通过蛇形走位 把原天线压缩到1/5 ... 结果令人非常难以接受 输入阻抗在谐振时候甚至只有2.3Ω

虽然这和实际我观察的情况有出入 但是基本还是表达了这个思想 因为大多数电流元互相抵消了 辐射功率大大下降 只有1/5电流元正常辐射 这样功率大概只有原来的 1/25 因为辐射太少 就等同一个长度1/4波长的波导开路了 回波几乎100% 接近短路
然而实际上 仍然有不少在用的类似的蛇形天线设备(大多数非偶振子 不过效果应该类似) 结果也没有这么糟糕
也许可以采用全波偶振子 利用0.5λ附近的高组区 通过串并感容的方法 获得合适的谐振点及阻抗 比如串入一个小电感 (或者利用杂散或者分布感容) 变成

并联个小电感 这是许多2.4G 倒F型天线的样子吧

或者使用高比例的巴伦

但是显然这些调整 都比较精细 即使预先仿真 只怕也需要不断实验调整 远没有直线型偶振子结构容错性高
注意 以上蛇形天线计算 并未考虑背板 如果使用背板 情况可能更复杂 但是总的来说 都是允许一部分能量出去 然后再想办法匹配
用平板电容法测过板子介电常数 并估计高频时候是5 (看来电木板比FR4板介电常数大)采用这个数据设计了天线长度 并简单蚀刻 (由于干膜太干 有些地方是拿记号笔修补的)
也许是幸运 随手绕个小巴伦做平衡 随手饶了两圈电感做匹配 只是试试的性质 就直接调到了450MHz 还有看起来不错的指标
可惜双频点的效果看不出来 也许靠太近了
其实等到上背板 指标应该会偏小 得调整 但是背板的理论部分我其实还没有搞定


还是认真做匹配看看 .,.. 嗯 这是理论侧
首先完善了一下前面的程序 (6.26: 发现k0_h计算有误 已更新)
Pythonimport scipy.integrate
import numpy
from matplotlib import pyplot
z0=50
wa=200
epsilon_eff=1.3
compress=0.2 # h/l
ratio_from=0
ratio_to=0.5
ratio_show=(ratio_from+ratio_to)/2
match=None
if True:
def match(z):
#@outport: C/parallel, @antenna: L/series, L=5.71213169610197e-09, C=2.113795485039202e-11
L=5.71213169610197e-09
C=2.113795485039202e-11
f=434.e6
w=2.j*numpy.pi*f
z=z+w*L
z=1/(w*C+1/z)
return z
#############################################
ratio=numpy.linspace(ratio_from+0.001, ratio_to-0.001, 1001)
k1_l=ratio*2*numpy.pi
# old wrong version : k0_h=k1_l*epsilon_eff*compress
# new right version : k1*l=k0*sqrt(epsilon_eff)*l -> k0*h=k1*l/sqrt(epsilon_eff)/l*h=k1_l/sqrt(epsilon_eff)*compress
k0_h=k1_l/numpy.sqrt(epsilon_eff)*compress
f=lambda theta, k1l, k0h: (((numpy.cos(k0h*numpy.cos(theta))-numpy.cos(k1l))/(((k0h*numpy.cos(theta))**2)-(k1l**2)))**2)*(numpy.sin(theta)**3)
r_sigma=numpy.vectorize(
lambda k1l, k0h: 60*((k1l*k0h)**2)*scipy.integrate.quad(f, 0, numpy.pi, args=(k1l, k0h))[0],
otypes=[float]
)(k1_l, k0_h)
r1_l=4*k1_l*r_sigma/(2*k1_l-numpy.sin(2*k1_l))
beta_a_l=r1_l/2/wa
t=wa/(numpy.cosh(2*beta_a_l)-numpy.cos(2*k1_l))
z=((numpy.sinh(2*beta_a_l)-beta_a_l/k1_l*numpy.sin(2*k1_l))-1j*(numpy.sin(2*k1_l)+beta_a_l/k1_l*numpy.sinh(2*beta_a_l)))*t
# with matching network
if match:
z=match(z)
print('At {}λ, RΣ={}, Z={}'.format(
ratio_show,
numpy.interp(ratio_show, ratio, r_sigma),
numpy.interp(ratio_show, ratio, z)))
fig, ax1=pyplot.subplots()
fig.subplots_adjust(right=0.6)
ax1.set_title('Input impedance of antenna')
ax1.set_xlabel('l/λ')
ax1.set_ylabel('Impedance (Ω)', color='black')
ax1.set_xlim(ratio_from, ratio_to)
ax1.set_xticks(numpy.linspace(ratio_from, ratio_to, 5))
ax1.grid()
plt1a=ax1.plot(ratio, numpy.real(z), linewidth=1, color='blue', label='Real')
plt1b=ax1.plot(ratio, numpy.imag(z), linewidth=1, color='red', label='Imag')
ax2=ax1.twinx()
ax2.set_ylabel('Phase (°)', color='orange')
ax2.set_ylim(-90, 90)
ax2.grid()
plt2=ax2.plot(ratio, numpy.degrees(numpy.angle(z)), linewidth=1, color='orange', label='Phase')
gamma=(z-z0)/(z+z0)
vswr=(1.+numpy.abs(gamma))/(1.-numpy.abs(gamma))
ax3=ax1.twinx()
ax3.spines['right'].set_position(('outward', 60))
ax3.set_ylabel('VSWR', color='black')
ax3.set_ylim(1, 5)
ax3.grid()
plt3=ax3.plot(ratio, vswr, linewidth=1, color='black', label='VSWR')
ax4=ax1.twinx()
ax4.spines['right'].set_position(('outward', 120))
ax4.set_ylabel('RΣ', color='cyan')
plt4=ax4.plot(ratio, r_sigma, linewidth=1, color='cyan', label='RΣ')
plts = plt1a+plt1b+plt2+plt3+plt4
ax3.legend(plts, [t.get_label() for t in plts], loc='upper right')
pyplot.show()在没有匹配之前 1/4λ处 阻抗非常的低 只有5欧左右

写了个程序来自动匹配 并且输出匹配后频率和匹配网络误差对匹配的影响
Pythonimport numpy
from matplotlib import pyplot
import scipy.integrate
z0=50.
zl=(5.372731854378172-0.09190623230437875j)
freq=434.e6
tolerance=0.2
method=None
C_first=True
L=None
C=None
match=None
'''
method='Customized, @outport: C/parallel, @antenna: L/series'
C_first=True
L=5.53e-9
C=24.e-12
def match(z, f, l, c):
w=2j*numpy.pi*f
z=z+w*l
return 1/(w*c+1/z)
'''
#resolve L/C if not specified
zr=numpy.real(zl)
zj=numpy.imag(zl)
if not method:
w=2*numpy.pi*freq
zr=numpy.real(zl)
zj=numpy.imag(zl)
if (zr<z0):
if C_first:
method='@outport: C/parallel, @antenna: L/series'
L=(numpy.sqrt(zr/(z0-zr))*(z0-zr)-zj)/w
C=1/w/(z0*numpy.sqrt(zr/(z0-zr)))
def match(z, f, l, c):
w=2j*numpy.pi*f
z=z+w*l
return 1/(w*c+1/z)
else:
method='@outport: L/parallel, @antenna: C/series'
C=1/w/(zj+numpy.sqrt(zr*(z0-zr)))
L=z0*numpy.sqrt(zr/(z0-zr))/w
def match(z, f, l, c):
w=2j*numpy.pi*f
z=z+1/(w*c)
return 1/(1/(w*l)+1/z)
else:
if C_first:
method='@outport: C/series, @antenna: L/parallel'
C=1/w/(numpy.sqrt(z0*(zr**2+zj**2-z0*zr)/zr))
L=(z0*zj+zr*numpy.sqrt(z0*(zr**2+zj**2-z0*zr)/zr))/(zr-z0)/w
def match(z, f, l, c):
w=2j*numpy.pi*f
z=1/(1/z+1/(w*l))
return z+1/(w*c)
else:
method='@outport: L/series, @antenna: C/parallel'
C=1/w/((numpy.sqrt(z0*zr*(zj**2+zr**2-z0*zr))-z0*zj)/(zr-z0))
L=numpy.sqrt(z0*zr*(zj**2+zr**2-z0*zr))/zr/w
def match(z, f, l, c):
w=2j*numpy.pi*f
z=1/(1/z+w*c)
return z+w*l
w=2*numpy.pi*f
print ('{}, L={}, C={}'.format(method, L, C))
###########################
def show(z, x, x_label):
gamma=(z-z0)/(z+z0)
vswr=(1.+numpy.abs(gamma))/(1.-numpy.abs(gamma))
fig, ax1=pyplot.subplots()
fig.subplots_adjust(right=0.75)
ax1.set_title('Impedance of matched')
ax1.set_xlabel(x_label)
ax1.set_ylabel('Impedance (Ω)', color='blue')
ax1.grid()
plt1a=ax1.plot(x, numpy.real(z), linewidth=1, color='blue', label='Real')
plt1b=ax1.plot(x, numpy.imag(z), linewidth=1, color='red', label='Imag')
ax2=ax1.twinx()
ax2.set_ylabel('Phase (°)', color='orange')
ax2.set_ylim(-90, 90)
ax2.grid()
plt2=ax2.plot(x, numpy.degrees(numpy.angle(z)), linewidth=1, color='orange', label='Phase')
ax3=ax1.twinx()
ax3.spines['right'].set_position(('outward', 60))
ax3.set_ylabel('VSWR', color='black')
ax3.grid()
ax3.set_ylim(1, 3)
plt3=ax3.plot(x, vswr, linewidth=1, color='black', label='VSWR')
plts = plt1a+plt1b+plt2+plt3
ax3.legend(plts, [t.get_label() for t in plts], loc='upper right')
#########################
tol=numpy.linspace((1.-tolerance), (1.+tolerance), 200)
f=tol*freq
z=match(zl, f, L, C)
show(z, f, 'Freq (Hz)')
l=tol*L
z=match(zl, freq, l, C)
show(z, l, 'L (H)')
c=tol*C
z=match(zl, freq, L, c)
show(z, c, 'C (F)')
##################################
pyplot.show()代入天线输入阻抗 计算出匹配电感5.7nH 电容21pF

再代入第一个程序看看效果 嗯 匹配上了

嗯 理论侧真好 ... 可是实践上 还有些问题要解决
巴伦很麻烦 尤其这个频段 做微带和传输线嫌大 做磁芯 手上没有好磁芯 本身弯折天线辐射效率就低 大多数能量感觉都浪费在磁芯耗损上了 但是不做平衡 背板就有不对称的问题
是不是可以找个偏离1/4λ的地方 使得正好匹配网络只需要一个元件 这个地方我感觉应该存在 下面试试看从理论上是否能找到
背板方面 暂时没有太大头绪 直接用应该没有问题 但有没有可能能优化 同相反射太复杂 用角铝做双反射结构有没有可能性
像楼主这样从基本电动力学出发来推导天线的,可能已经非常稀有了。我大概只在电磁学课程的习题里,观摩过一些基于极简单情况的推导。
“其次是"耗损电阻平均分布在振子上"这个前提可能不对”
这里的损耗是指辐射损耗还是电阻损耗?如果是辐射损耗,那么这个“电阻”我理解不在天线的任何地点,而在天线的整体(即对外辐射带来的阻尼)。如果是电阻损耗,那么因为各处电流不同,损耗肯定也是各处不同的。
我猜测你说的蛇形线,电流元辐射相互抵消,导致辐射效率低是个根因。业界(先声明一下,我不在业界 )的做法应该是加感谐振,这样能有效缩短天线长度,没有蛇形线,不会相互抵消。加感天线长度短带来的辐射下降,被谐振以后从电感到天线末端的电流增强所抵消,所以可以维持高辐射效率。
)的做法应该是加感谐振,这样能有效缩短天线长度,没有蛇形线,不会相互抵消。加感天线长度短带来的辐射下降,被谐振以后从电感到天线末端的电流增强所抵消,所以可以维持高辐射效率。
4,5百MHz的balun,用细同轴线弯成螺线管可能也可以对付。
程序没时间看了,不评论了。
像楼主这样从基本电动力学出发来推导天线的,可能已经非常稀有了。我大概只在电磁学课程的习题里,观摩过一...
这个耗损电阻R1 是已经考虑到电流分布 从不带电流分布的R∑上推导出来的 正因为R1平均分布 才有各处电流不同 辐射也不同的效果
今天做了个简单测试 (之前仪器的校正堵头被猫叼不知道哪里去了 今天才在冰箱下面找到 这个理由不错吧) 然后发现与前面计算的误差较大 检查程序 发现程序中k0_h式子错了 然后重新推导修改
Pythonimport scipy.integrate
import numpy
from matplotlib import pyplot
z0=50
wa=367
epsilon_eff=1.2
compress=0.2 # h/l
ratio_from=0
ratio_to=0.5
ratio_show=(ratio_from+ratio_to)/2
match=None
if False:
def match(z):
#@outport: C/parallel, @antenna: L/series, L=5.71213169610197e-09, C=2.113795485039202e-11
L=5.71213169610197e-09
C=2.113795485039202e-11
f=434.e6
w=2.j*numpy.pi*f
z=z+w*L
z=1/(w*C+1/z)
return z
#############################################
ratio=numpy.linspace(ratio_from+0.001, ratio_to-0.001, 1001)
k1_l=ratio*2*numpy.pi
# k1*l=k0*sqrt(epsilon_eff)*l -> k0*h=k1*l/sqrt(epsilon_eff)/l*h=k1_l/sqrt(epsilon_eff)*compress
k0_h=k1_l/numpy.sqrt(epsilon_eff)*compress
f=lambda theta, k1l, k0h: (((numpy.cos(k0h*numpy.cos(theta))-numpy.cos(k1l))/(((k0h*numpy.cos(theta))**2)-(k1l**2)))**2)*(numpy.sin(theta)**3)
r_sigma=numpy.vectorize(
lambda k1l, k0h: 60*((k1l*k0h)**2)*scipy.integrate.quad(f, 0, numpy.pi, args=(k1l, k0h))[0],
otypes=[float]
)(k1_l, k0_h)
r1_l=4*k1_l*r_sigma/(2*k1_l-numpy.sin(2*k1_l))
beta_a_l=r1_l/2/wa
t=wa/(numpy.cosh(2*beta_a_l)-numpy.cos(2*k1_l))
z=((numpy.sinh(2*beta_a_l)-beta_a_l/k1_l*numpy.sin(2*k1_l))-1j*(numpy.sin(2*k1_l)+beta_a_l/k1_l*numpy.sinh(2*beta_a_l)))*t
# with matching network
if match:
z=match(z)
print('At {}λ, RΣ={}, Z={}'.format(
ratio_show,
numpy.interp(ratio_show, ratio, r_sigma),
numpy.interp(ratio_show, ratio, z)))
fig, ax1=pyplot.subplots()
fig.subplots_adjust(right=0.6)
ax1.set_title('Input impedance of antenna')
ax1.set_xlabel('l/λ')
ax1.set_ylabel('Impedance (Ω)', color='black')
ax1.set_xlim(ratio_from, ratio_to)
ax1.set_xticks(numpy.linspace(ratio_from, ratio_to, 5))
ax1.grid()
plt1a=ax1.plot(ratio, numpy.real(z), linewidth=1, color='blue', label='Real')
plt1b=ax1.plot(ratio, numpy.imag(z), linewidth=1, color='red', label='Imag')
ax2=ax1.twinx()
ax2.set_ylabel('Phase (°)', color='orange')
ax2.set_ylim(-90, 90)
ax2.grid()
plt2=ax2.plot(ratio, numpy.degrees(numpy.angle(z)), linewidth=1, color='orange', label='Phase')
gamma=(z-z0)/(z+z0)
vswr=(1.+numpy.abs(gamma))/(1.-numpy.abs(gamma))
ax3=ax1.twinx()
ax3.spines['right'].set_position(('outward', 60))
ax3.set_ylabel('VSWR', color='black')
ax3.set_ylim(1, 5)
ax3.grid()
plt3=ax3.plot(ratio, vswr, linewidth=1, color='black', label='VSWR')
ax4=ax1.twinx()
ax4.spines['right'].set_position(('outward', 120))
ax4.set_ylabel('RΣ', color='cyan')
plt4=ax4.plot(ratio, r_sigma, linewidth=1, color='cyan', label='RΣ')
plts = plt1a+plt1b+plt2+plt3+plt4
ax3.legend(plts, [t.get_label() for t in plts], loc='upper right')
pyplot.show()使用背板远离的参数 然后结果居然吻合得不错


计算得2.66Ω 实测是2.82Ω 测试时候背板远离 使用了一个电流共轭型的1:1巴伦 实际上也曾经用非平衡式测试 只测一端 实测非平衡单端电阻与平衡两端电阻接近但还略小 说明了做非平衡-平衡转换时 是有耗损的 毕竟辐射功率不变 测出来电阻越大 说明有些能量非辐射性地消耗掉了
上背板后 因为等效介电常数上升 同样长度天线 谐振点频率变低 这个符合预期

但是实测电阻变大了太多 要知道 用背板后的参数 计算出来的电阻应该更小

2.13Ω和3.16欧姆就相差太大了 何况我原本预期 辐射功率应该只有一半 理应更小才对 说明背板会带来极大问题 我测试时候 是用根天线同时检查S21参数的 用了背板 S21下降了10db左右 说明消耗功率提高了 真实辐射反而变小了 这样即使匹配了阻抗也于事无补
可以说原方案定向的意图是失败了 但是网上确实有卖非常薄不可能是反射结构的同频平板天线 我得暂停这个方案 再考虑看看有什么办法
那些是patch antenna吧
毕竟网上也找不到平板定向天线的资料 只能自己想象了
楼主搜索的姿势可能不太对。
引用信仰は儚き人間の為に发表于12楼的内容那些是patch antenna吧毕竟网上也找不到平板定向天线的资料 只能自己想象了楼主搜索的姿势可...
啊 我搜了一下 有可能的 谢谢提醒
---------
学习了patch antenna 从市售产品尺寸来看 应该是这种天线类型不错了 等效为两条缝隙天线组成的天线阵
可惜尺寸太大了 长宽都需要1/2波长左右 我没有这么大的板材 做出来也太大了 但是其中缝隙天线的原理给我不少启示 我看看有什么办法缩小化
尝试缝隙天线方向 花了半小时 手刻带背胶的铜箔做了一个实验 简单LC匹配了一下 没想到特征这么典型 尤其是S21 带外很“干净”

但是就是S21还是太低 离我希望的差了至少15dB 但是有点希望了
。。。。。6.28。。。。
还是不行 此类设计依然不能兼容背板的存在 依然除非背板够远
也研究了贴片天线的弯折化 但是贴片元件的根本原理 即使不考虑对外的双缝隙阵列效果 也必须E场在反射后回来正好同相(开口处谐振出很高的E场) H场正好反向(等于开口处位移电流近0) 除非整面弯折 或者做成非常精巧的弯折波导 这难度太大了
。。。。。6.29。。。。
整面弯折也许也没那么难 如果只弯几下 虽然不是“平面”天线了 也许也能接受 可以考虑3D打印 然后贴铜箔 甚至金箔 电镀
缩小化的话 原本的双缝阵列就没有意义了 首先至少可以裁掉一半 双头蛇型变成阑尾型 利用短路反射 E场H场反射回去正好与出口处同相 这么一想 至少能小型化一半了 300mm 变成 150mm 加工都容易很多了

立即测试贴片天线的弯折化 使用双面板做贴片 单缝隙 用铜箔短路和做弯折处转承 随便靠近短路点越1/4总长度处馈入 只用40mm*100mm的大小尺寸 186MHz处 得到感觉不错的天线效率 此时驻波比上升1.5倍的带宽是2MHz


因为直接用双面板做传输线 等效介电常数很高 所以才能在这么小的尺寸实现远超预期的186MHz 经过计算 频率也大致相符 缺点是带宽非常窄 仅仅够精细调整后的单频点应用

后面又测了单块90mm的板子 频率344MHz 带宽4MHz (驻波比上升1.5倍)
但是如果采用空气介质 板间距5mm 预期占用90mm空间 将是不错的尺寸 要知道 这个尺寸下的铝板 网上首单价1块钱就可以买几块了
这种单缝隙天线的阻抗也不难计算
草率了 抱歉 路上想了各种可以简化计算的模型 发现均有漏洞 想硬做积分 发现这得搞一个3维的 与一维电流元天线相比 复杂度远远超出可行性
网上最简单的计算方法 也是对偶出一维磁流元再算 即使如此 结果也很复杂 抄一个等效导纳的经验公式

--------------------- 6.30 -------------------------
!!! 上面抄的公式依然有问题 从其推导看 因为双缝隙的远场与单缝隙有区别 应该并不完全合适单缝隙情况 !!!!!!!!!!!!
只能耐心推导了 反正今天下大雨 为了简化 当它是z轴上一个长w的一维的细缝 远场某处 使用球坐标 距离原点r r矢与z轴交角为θ 其投影在xy平面与x轴交角为φ 因为是定向半边 所以φ只用积一半
假设缝隙处处电场均等 振幅为V0/h 那么对应得磁流密度也是 V0/h 对于全开放空间 磁流就是V0 但是由于这是缝口 半开放的 磁流等效为 2V0 在短路处的反射 有以下磁流对应的远场公式

Python>>> from sympy import symbols,integrate,cos,sin
>>> w,j,k0,z,theta=symbols('w,j,k0,z,theta')
>>> r=integrate(cos(k0*z*cos(theta))+j*sin(k0*z*cos(theta)), (z, -w/2, w/2), conds='none')
>>> print(r.simplify())
2*sin(k0*w*cos(theta)/2)/(k0*cos(theta))下面的积分没法化简成普通的函数 使用40mm宽度缝隙 434MHz 实际算一下
Python>>> import math
>>> import scipy.integrate
>>> lbd=3e8/434e6
>>> k0=2*math.pi/lbd
>>> w=0.04
>>> 120.*math.pi**2/scipy.integrate.quad(lambda theta:math.sin(theta)*(math.tan(theta)*math.sin(k0*w*math.cos(theta)/2))**2, 0, math.pi)[0]
26936.532390360382
>>> 90*(lbd/w)**2
26877.29618382212
>>> w=4
>>> 120.*math.pi**2/scipy.integrate.quad(lambda theta:math.sin(theta)*(math.tan(theta)*math.sin(k0*w*math.cos(theta)/2))**2, 0, math.pi)[0]
21.48979101115975
>>> 120*lbd/w
20.737327188940093发现无论缝隙宽度是小于波长还是很巨大 都与抄的公式基本接近 所以 以上演算应该没有问题 也说明双缝隙的远场与单缝隙还是很接近的
在一般情况下 由于是1/4波长处短路 等效在开口处开路 所以在缝口处的输入阻抗可以就用RΣ 否则就需要根据传输线阻抗变换之类的方法去分析了
还有一些有用的计算公式 比如贴片天线的有效长度公式 设计时候需要用到 但是对于1/4波长天线 不需要2ΔL 一份就足够

此外还有馈线点的公式 (错误的!!!!)

但是我不记得在哪个国外网站看到 说这个网上到处用的公式 其实只合适同轴线探针馈电模型 如果是插入式馈电设计 需要使用cos的4次方而不是2次方 一时间找不到记忆的具体来源 这里先记录一下
疏忽了 上面抄的馈线点公式 也不合适单缝情况 根据驻波符合正弦分布
由
----------- 7.1 补充 ------------
上面这个式子 是从能量的角度推导的 并不能表现阻抗中的复数部分 如果从传输线阻抗变换的角度硬算 是可以得到复阻抗的 方便进一步匹配
Python>>> from sympy import symbols, tan, pi
>>> z0,r,k1,l1=symbols('z0,r,k1,l1')
>>> y=1/(1/(1j*z0*tan(k1*l1))+(z0+1j*r*tan(pi/2-k1*l1))/z0/(r+1j*z0*tan(pi/2-k1*l1)))
>>> y.simplify()
0.5*(r*tan(k1*l1) + I*z0)*sin(2*k1*l1)这就有点尴尬了 我暂时也不知道怎么让sympy使用倍角公式继续简化结果 但是人工可以算出 其实数部分 和能量方式推出的R(x) 其实是一致的 而其虚数部分则是
Zc是传输线的特征阻抗 一般比较低 所以阻抗中的虚数部分是很小的 再考虑到其实RΣ其实本身也忽略了虚数部分 因此这个结果其实意义不大
---------------------------------
写了个程序模拟其带宽 (7.1更新 馈入点改用传输线阻抗变换算法 结果区别不大)
Pythonimport scipy.integrate
import numpy
from matplotlib import pyplot
z0=50
w=0.008
h=0.0016
epsilon=4.5
freq=434e6
scope=0.002
feed=None
match=None
if False:
def match(z, f):
#@outport: L/series, @antenna: C/parallel, L=1.4525860662263755e-07, C=9.112836049098965e-13
L=1.3225860662263755e-07
C=10e-13
w=2.j*numpy.pi*f
z=1/(1/z+w*C)
z=z+w*L
return z
################################
numpy.seterr(all='warn')
def r_int(theta, k0, w):
return numpy.sin(theta)*(numpy.tan(theta)*numpy.sin(k0*w*numpy.cos(theta)/2))**2
@numpy.vectorize
def r_func(k0, w):
return 120.*numpy.pi**2/scipy.integrate.quad(r_int, 0, numpy.pi, args=(k0, w))[0]
epsilon_eff=(epsilon+1.)/2+(epsilon-1.)/2/numpy.sqrt(1+12.*h/w)
zc=120*numpy.pi/numpy.sqrt(epsilon_eff)/(w/h+1.393+0.667*numpy.log(w/h+1.444))
delta_l=0.412*h*(epsilon_eff+0.3)*(w/h+0.264)/(epsilon_eff-0.258)/(w/h+0.8)
lbd=299792458./freq
k0=2*numpy.pi/lbd
k1=k0*numpy.sqrt(epsilon_eff)
l=lbd/4/numpy.sqrt(epsilon_eff)
r_sigma=r_func(k0, w)
if not feed:
feed=numpy.arcsin(numpy.sqrt(z0/r_sigma))*2*l/numpy.pi
#z=r_sigma*numpy.sin(numpy.pi*feed/2/l)**2
z=1/((zc+1j*r_sigma*numpy.tan(k1*(l-feed)))/(r_sigma+1j*zc*numpy.tan(k1*(l-feed)))/zc
-1j/(zc*numpy.tan(k1*feed)))
if match:
z=match(z, freq)
print(f'epsilon_eff={epsilon_eff}, zc={zc}')
print(f'Length={l}, ΔLength={delta_l}, r_sigma={r_sigma}')
print(f'feed={feed}, z={z}')
########################################
f=numpy.linspace(freq*(1-scope), freq*(1+scope), 1001)
lbd=299792458./f
k0=2*numpy.pi/lbd
k1=k0*numpy.sqrt(epsilon_eff)
z=r_func(k0, w)
#z=1./(1./z-1.j/(zc*numpy.tan(f/freq*numpy.pi/2)))
#z=z*numpy.sin(numpy.pi*feed/2/l)**2
z=1/((zc+1j*z*numpy.tan(k1*(l-feed)))/(z+1j*zc*numpy.tan(k1*(l-feed)))/zc
-1j/(zc*numpy.tan(k1*feed)))
if match:
z=match(z, f)
fig, ax1=pyplot.subplots()
fig.subplots_adjust(right=0.6)
ax1.set_title('Input impedance of antenna')
ax1.set_xlabel('Freq')
ax1.set_ylabel('Impedance (Ω)', color='black')
ax1.set_xlim(freq*(1-scope), freq*(1+scope))
ax1.set_xticks(numpy.linspace(freq*(1-scope), freq*(1+scope), 5))
ax1.grid()
plt1a=ax1.plot(f, numpy.real(z), linewidth=1, color='blue', label='Real')
plt1b=ax1.plot(f, numpy.imag(z), linewidth=1, color='red', label='Imag')
ax2=ax1.twinx()
ax2.set_ylabel('Phase (°)', color='orange')
ax2.set_ylim(-90, 90)
ax2.grid()
plt2=ax2.plot(f, numpy.degrees(numpy.angle(z)), linewidth=1, color='orange', label='Phase')
gamma=(z-z0)/(z+z0)
vswr=(1.+numpy.abs(gamma))/(1.-numpy.abs(gamma))
ax3=ax1.twinx()
ax3.spines['right'].set_position(('outward', 60))
ax3.set_ylabel('VSWR', color='teal')
ax3.set_ylim(1, 5)
ax3.grid()
plt3=ax3.plot(f, vswr, linewidth=1, color='teal', label='VSWR')
plts = plt1a+plt1b+plt2+plt3
ax3.legend(plts, [t.get_label() for t in plts], loc='upper right')
pyplot.show()其理论带宽真是窄得令人发指啊

即使是空气介质 一样不够用

当缝隙长度达到接近1/2波长时候 带宽才比较够用 接近中心频率的1%

幸好实际上会有各种不理想的情况 无法计算的杂7杂8效应 否则与其当天线 还不如当晶振用了
也许把缝隙前沿改成三角形 梯形 椭圆型等等 可以改善带宽
---------
后面又想了想 以上程序在带宽方面没什么指导意义 实际情况比上述好得多 上面的窄带宽来源于“完美”传输线的特性 但是这么一个扁盒子 其实际的谐振品质应该不高 比如说从光从馈点到各处边 就有不同长度的传播/反射路径的可能 如果有空学习这方面的知识后再修改吧
又看了一下,感觉楼主这样用远场坡印亭矢量积分算辐射电阻的做法有问题。因为并没有计算那个接地金属板上的感应电流的远场。如果那个金属板是无穷大可能还好,可以假设是个理想电壁,当另一边有个镜像天线来处理就好了。但是这相对天线有限大的板,怎么算,我不清楚。
又看了一下,感觉楼主这样用远场坡印亭矢量积分算辐射电阻的做法有问题。因为并没有计算那个接地金属板上的...
目前除了仿真 只怕没人不把接地金属板当无穷大处理的
上面的计算是以磁偶极子为基础的 认为传输线上的电流互相抵消 仅计算开口处的电压等效磁流(电流的对偶)所谓接地金属板 是当成传输线用的 各处电位除了馈电处 不能当地 没有无穷大的事情 应该影响到传输线那部分 影响等效介电系数之类 此外还有电磁绕射问题 但是感觉除了仿真 很难追究下去了
我这里也没有用镜像天线法 这方面我对电磁处理的原则有些疑虑 感觉镜像法不能当完全的镜像用 否则我就不另行自己推导单缝情况了 如果镜像出另一条缝 可以直接采用网上的资料(正如弯折天线的资料也没有 我才自己推导)
但是镜像出来另一条缝 按理会出现天线阵列效应 (这也是网上典型贴片的计算基础)但是此处应该没有 因为这个在短路处的“镜”是很狭窄的 并不是无穷大的“镜” 对外影响应该可以忽略
理论需要联系实际 15楼的理论虽然看起来不错 但是与实测相差实在太远 比如在一块 40mm*86mm*1.6mm的测试板上 馈电在31mm处 理论上频率是425MHz 应该测到电阻为8k+3j 带宽极窄 如下图

但是 实测效果却是这样的

频率相差不大 可以认为是设定的介电常数有误差 缩短效应比预想的略大等 但是实测电阻和带宽居然可以相差近数十倍 这就毫无指导意义了
我认为这个原因应该有:
实际上我这里并没有足够的背板尺寸(比波长小很多) 导致辐射可以绕射到后方而不是 因此实际远场辐射近乎大一倍 等效于电阻小一倍 这个因素在实际中很难衡量 可以采用一个因子 Cd =1~2 来弥补
损耗 毕竟在理论推导中 没有考虑这一因素 等于谐振电路的品质为无穷大 但是实际并非如此 这个损耗可以等同于天线处并了一个电阻
趋肤效应带来的铜耗 : 经过计算 在400M左右趋肤深度3μm 虽然只有铜箔厚度的1/10 但是考虑到是大面积铺铜 在这个尺寸的天线下 可以不用考虑
传输线电感的磁耗 : 也暂时不考虑
内外介质不同造成的表面波耗损: 因为内外介质介电常数相差甚大 这个确实影响非常大 但是没有大到这个地步
覆铜板介电材料的耗损: 内介质介电常数越大 相同辐射下 驻波能量就会越大 带来的耗损也越大
着重考虑 2.d 设天线长L 宽W 介质等效介电常数
等效到缝隙处的电阻为
我也不知道测试板的耗损角正切 但是从嘉立创那里查到他们用的电路板资料


对于本实测 代入得 477欧 相比天线的8k而言 使得天线效率极为低下
修改程序 增加绕射系数(此例直接为2) 增加介质耗损计算后 得到结果如下

仔细对比实测屏幕和此图 可以看到 无论是带宽表现 输入阻抗等 实测与计算间的误差已经够小 足够进行实用的指导了
但是从图上看出 尚有一部分未考虑到的耗损在内 使得计算的阻抗比实测还是略高 我认为这是目前我尚无能力分析的表面波耗损 从网上一些文章来看 我这种高介电常数的 应该影响也颇大 如果我找到有用的经验公式 再加进去吧 目前看来有20%的耗损 比较属于鸡肋 为此努力不值得 不做什么又觉得有点亏
因为15楼的过程中删改太多 干脆这里归纳一下 (注意只针对1/4波长天线类型而非1/2波长的)
从理论上说 完美的平行板传输线特征阻抗是
经验修正公式为 (Microwave Engineering, Pozar David M., Fourth Edition))
W 随意 但是如果超过波长的1/2 需要注意避免W方向的驻波 W太小 天线效率也低
h 随意 但是据称实践中取0.02λ最好 天线效率最高 尤其注意 低于0.02λ 效率会急剧下降
修改后的程序
Pythonimport scipy.integrate
import numpy
from matplotlib import pyplot
z0=50
w=0.04
h=0.0016
epsilon=4.7
freq=410e6
span=20e6
feed=0.031
match=None
coef_diffraction=2.
loss_tangent=0.02
if False:
def match(z, f):
#@outport: L/series, @antenna: C/parallel, L=2.214142593172209e-08, C=3.930538829868875e-12
L=2.214142593172209e-08
C=3.930538829868875e-12
w=2.j*numpy.pi*f
z=1/(1/z+w*C)
z=z+w*L
return z
################################
numpy.seterr(all='warn')
def r_int(theta, k0, w):
return numpy.sin(theta)*(numpy.tan(theta)*numpy.sin(k0*w*numpy.cos(theta)/2))**2
@numpy.vectorize
def r_func(k0, w):
return 120.*numpy.pi**2/scipy.integrate.quad(r_int, 0, numpy.pi, args=(k0, w))[0]/coef_diffraction
epsilon_eff=(epsilon+1.)/2+(epsilon-1.)/2/numpy.sqrt(1+12.*h/w)
zc=120*numpy.pi/numpy.sqrt(epsilon_eff)/(w/h+1.393+0.667*numpy.log(w/h+1.444))
delta_l=0.412*h*(epsilon_eff+0.3)*(w/h+0.264)/(epsilon_eff-0.258)/(w/h+0.8)
lbd=299792458./freq
k0=2*numpy.pi/lbd
k1=k0*numpy.sqrt(epsilon_eff)
l=lbd/4/numpy.sqrt(epsilon_eff)
r_loss1=h/numpy.pi/freq/epsilon/8.854187817e-12/w/l/loss_tangent
r_sigma=r_func(k0, w)
z=1/(1/r_loss1+1/r_sigma)
if not feed:
feed=numpy.arcsin(numpy.sqrt(z0/z))*2*l/numpy.pi
z=1/((zc+1j*z*numpy.tan(k1*(l-feed)))/(z+1j*zc*numpy.tan(k1*(l-feed)))/zc
-1j/(zc*numpy.tan(k1*feed)))
if match:
z=match(z, freq)
z00=z
print(f'epsilon_eff={epsilon_eff}, zc={zc}')
print(f'Length={l}, ΔLength={delta_l}')
print(f'r_sigma={r_sigma} r_loss1={r_loss1}')
print(f'feed={feed}, z={z}')
########################################
f=numpy.linspace(freq-span/2, freq+span/2, 1001)
lbd=299792458./f
k0=2*numpy.pi/lbd
k1=k0*numpy.sqrt(epsilon_eff)
z=r_func(k0, w)
z=1/(1/r_loss1+1/r_sigma)
z=1/((zc+1j*z*numpy.tan(k1*(l-feed)))/(z+1j*zc*numpy.tan(k1*(l-feed)))/zc
-1j/(zc*numpy.tan(k1*feed)))
if match:
z=match(z, f)
fig, ax1=pyplot.subplots()
fig.subplots_adjust(right=0.6)
ax1.set_title('Input impedance of antenna')
ax1.set_xlabel('Freq')
ax1.set_ylabel('Impedance (Ω)', color='black')
ax1.set_xticks(numpy.linspace(freq-span/2, freq+span/2, 5))
ax1.grid()
plts=ax1.plot(f, numpy.real(z), linewidth=1, color='blue', label='Real')
plts+=ax1.plot(f, numpy.imag(z), linewidth=1, color='red', label='Imag')
ax2=ax1.twinx()
ax2.set_ylabel('Phase (°)', color='orange')
ax2.set_ylim(-90, 90)
ax2.grid()
plts+=ax2.plot(f, numpy.degrees(numpy.angle(z)), linewidth=1, color='orange', label='Phase')
gamma=(z-z0)/(z+z0)
vswr=(1.+numpy.abs(gamma))/(1.-numpy.abs(gamma))
gamma00=(z-z00)/(z+z00)
vswr00=(1.+numpy.abs(gamma00))/(1.-numpy.abs(gamma00))
ax3=ax1.twinx()
ax3.spines['right'].set_position(('outward', 60))
ax3.set_ylabel('VSWR', color='teal')
ax3.set_ylim(1, 5)
ax3.grid()
plts+=ax3.plot(f, vswr, linewidth=1, color='teal', label='VSWR')
plts+=ax3.plot(f, vswr00, linewidth=1, color='darkgreen', label='VSWR00')
ax3.legend(plts, [t.get_label() for t in plts], loc='upper right')
pyplot.show()这里不得不说 虽然进行得比较深入了 但是我得说 在这个频段 贴片天线有许多不足
尺寸比普通线型天线大 毕竟一个2维得 一个1维的
介电介质质耗损对天线效率有太大影响 普通人很难准备合适的介电介质 使用空气介质 又会让尺寸进一步变大
虽然可以定向 但是如果考虑电波绕射问题 尺寸还需要更进一步变大
而我虽然没有在标题上加上尺寸限制 但是一直是我考虑的重点 所以 大概这个项目是失败了会放弃 (因为如果用空气介质 即使使用对角线反射型的天线 尺寸也超过了100mm 需要重新购买 而且对大东西感觉不喜) 虽然学到了不少东西
今天做了两个天线 其中一个是两块100mm*100mm 的铝板构成 相距约13mm 在20mm处馈线 为了不伤板 馈线采用贴铜箔方式 所以阻抗虚数部分需要忽略它

从结果看 阻抗还是相当符合预期 空气带来的损耗就很小了 但是带宽依然不错 比预期要好
另外有一个阻抗达1.4k的高峰不知道成因 可能与我馈线接法有关 毕竟不是从中心馈入 又拉得老长 不过从S21看没有利用的价值
另一个天线就一言难尽了 也许是受到“万物皆可卷”的哲思影响 也许是想到趋肤深度反正才几微米 做出的一个变形 用的是软铝皮


想来也可能因为其非对称性 有部分电流元天线的作用 指标出乎预料的不错 就是需要狠狠匹配 毕竟即便我都接到了很靠短路点的地方了 阻抗依然有1k 这显然并不能只用贴片天线的理论解释 毕竟从尺寸看 缝隙处的阻抗也不超过1k
但是不管形状怎么样 理论多难分析 既然能谐振 能形成驻波 就有成为天线的潜力 过几天认真做一块这样的天线看看
今天做了两个天线 其中一个是两块100mm*100mm 的铝板构成 相距约13mm 在20mm处馈线...
看你的尺子和铝箔的关系,馈电点距离左边铝箔短路处大概4CM,这不能以500MHz的1/4波长电抗变换来理解。因为500M的四分之一波长大概150mm,超过了4cm。
我想大概或许可能是这样:馈电点左边短路,构成了个电感。右边开路,构成了个电容。LC并联,在500M谐振了。当然这是近似的,考虑到深度方向还有很深,所以带宽被展宽了。
今天做了两个天线 其中一个是两块100mm*100mm 的铝板构成 相距约13mm 在20mm处馈线...
从最左边的短路点,沿着两张铝箔的中间往右走,跨过馈电点,走到最右边,再往上折,再往左折,直到开口处,这就是个传输线。你这是在一端短路一端开路的1/4波长谐振传输线中间的某个点馈电。

是的 没错啊 机制就是这样的 在哪个点馈电 阻抗有所不同 与开口处辐射阻抗 是馈电距离比例的正弦平方关系
按理应该较小 但是由于这种结构 不能简单简单等同你画的那张图 所以才不一样
有可能等同这样的

200字以内,仅用于支线交流,主线讨论请采用回复功能。