这当然是抽离实际的复杂 仅对皮带弹性和松弛方面的简单的分析 纯粹出于某些简单的前提假设 没有实验验证 我也不敢以偏概全
按理如果皮带张力良好的情况下 其实倒不用太在意太多
这里只考虑传送皮带因为弹性和松弛造成的误差 并且假设1单位长度的皮带 因此造成过长的长度为d 意思是理想长度为1的皮带 实际长度是1~(1+d)
这里也假设所有结构的边长为1 打印头停在最中间(设为xy坐标原点) 离各边均为0.5 不考虑构件尺寸带来的实际少量尺寸偏差 只考虑打印头在此处的误差
1.先看corexy结构吧 如图
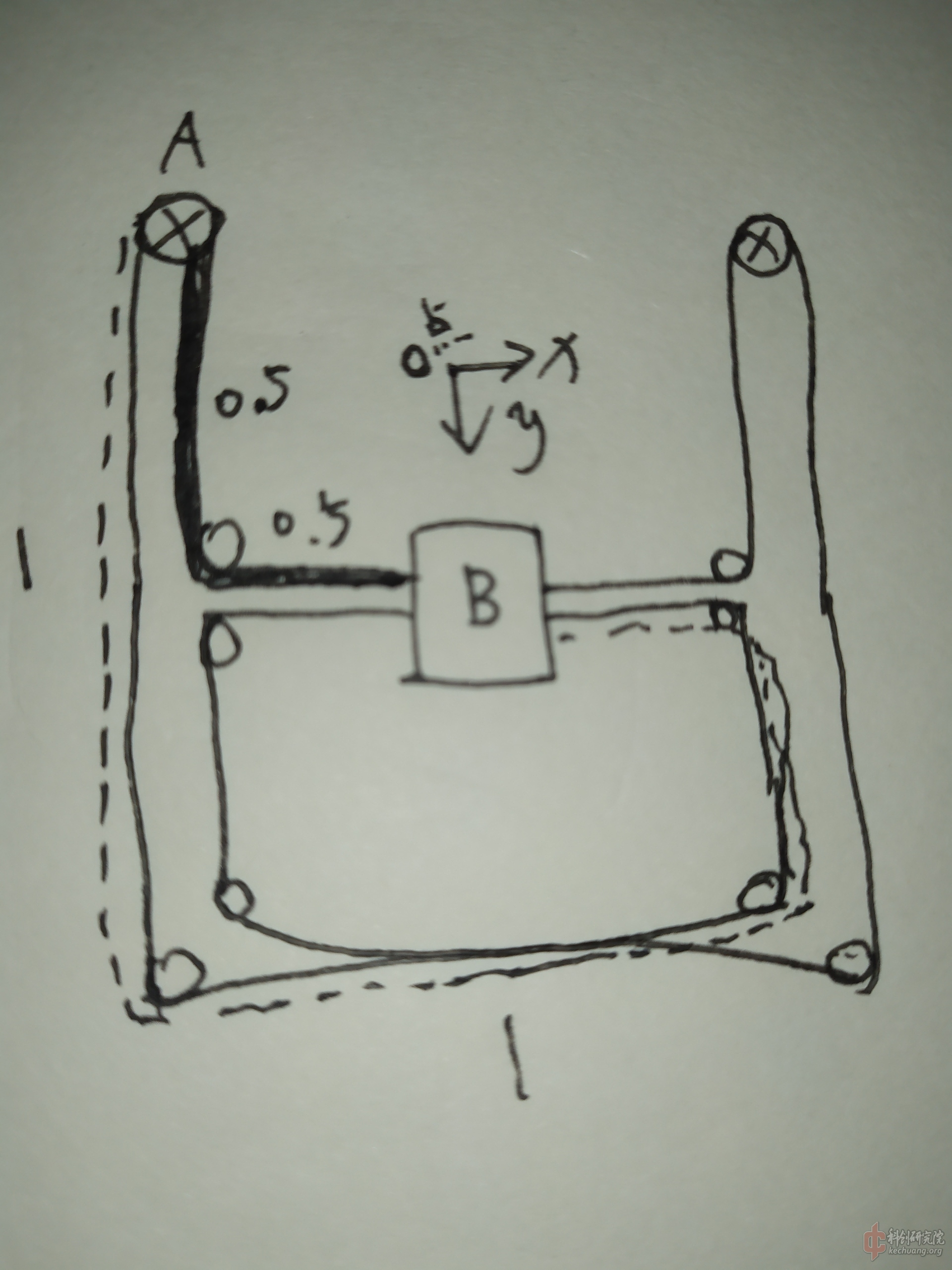
考虑图上加粗的一段线 这是马达A到滑块B的约束性传动带 这段线理想应该长度为1 但是因为松弛 实际可能最多比理想长为d 因此B可以超出约束位置 多往右方或者下方偏移造成误差 假设B因此往右偏移为x 往下偏移为y 实际的约束变成
x+y < d
再考虑虚线跟随那段线 长度为3 可能松弛为3d 会造成B往左往上偏移 所以推出
-x-y < 3d
综合可以知道
-3d < x+y < d
另外两根线也类似分析 得到
-d < x-y < 3d
这两组实际4个不等式 围起来一个误差区域 如图

这块误差区域面积为8 需要注意的是 误差中点并不在原点 并不均衡 具有固定y向偏移-1
标准corexy respin的分析结果和标准corexy一样
2.corexy的blv变形结构 该结构将马达放在传动带的中间 缺点是需要改进的结构 让传动带包围传动齿轮更好 如图

推导出的不等式为
-2d < x+y < 2d
-2d < x-y < 2d

这块误差区域面积边长等均与标准corexy相同 但是没有误差中心偏移(如果打印头不在整个结构中间 仍然会有误差中心偏移)
3.hbot结构 如图

这个结构只有3个约束 立不出4个不等式 推导出
y < d (约束1可放长2d 再均分到左右两边传动带)
x-y < 2d
-x-y < 2d

这个误差范围是个三角形 面积为9 虽然比corexy大了1/8 但是考虑到结构更简单 而且没有固定的误差偏移 个人觉得比corexy更好 如果做corexy就做blv的才有收益
4. mb um i3等结构类似 都是x y独立各自驱动

-1.5d < x <0.5d
-1.5d < y < 0.5d

最简单的传动线路带来最高的精度 误差范围面积只有4 远小于corexy和hbot 所以不要瞧不起
此后两者的优点其实在于结构好看 马达不给滑块带来惯性影响 而不在精度
仍然有误差中点的偏差问题 如果将马达放在传动带中间 使其两边两段传动带到滑块的位置相同 可以解决此问题 但从未见此种设计实用
5.三角洲结构 从传动带带来的误差而言 应该和以上mb等相似 但是这种结构不流行了
6. T杆 滚珠杆的就不说了 精度虽然没得说 但是没必要
200字以内,仅用于支线交流,主线讨论请采用回复功能。