为啥23的表可以这么乘。。。这样乘出来是在所有情况下确实是蓝车并且辨认为蓝车的概率,就算按第二个表的话也应该是取第一列0.12/(0.12+0.17)=0.43
1和4的分歧在于1中“正确辨认蓝车的概率”是辨认出蓝车的情况下确实是蓝车的概率,4中是确实是蓝车的情况下辨认为蓝车的概率。。
如果按4理解的话,若“正确辨认的概率”为0,那就是在任何情况下此人遇到蓝车就辨认为绿车,遇到绿车就辨认为蓝车,辨认到蓝车时确实是蓝车的概率自然是0.
偶然看到的,题目如下:
1.一辆出租车肇事逃逸了,一个目击者认出那辆车的颜色是蓝色的。
2.已知所在城市有两个出租车公司,一个公司的出租车是绿色的,另一个公司的出租车是蓝色的。绿出租车公司拥有85%的出租车,蓝出租 车公司拥有15%的出租车。
3.经测试表明:该目击者可正确辨认车是蓝色的概率是80%,不能正确辩认的概率是20%。
问.肇事车辆是蓝色而不是绿色的概率是多少?
看上去很简单是吧?
以下收录找到的三种解法:
1.题目化简为:
目击者判断车是蓝色的,且目击者有80%概率判断正确
所以答案显而易见,就是80%!简单!
好像很有道理啊有没有!
2.我觉得没那么简单!
列一个表:
| 情况 | 实际是蓝色 | 实际是绿色 |
| 看到是蓝色 | 80%*15%=12% | 20%*85%=17% |
| 看到是绿色 | 20%*15%=3% | 80%*85%=68% |
所以正确答案应该是15%!哈哈哈!
好像很有道理啊有没有!
3.楼上的表是啥玩意!
| 情况 | 实际是蓝色 | 实际是绿色 |
| 看对 | 80% | 0% |
| 看错 | 15%*20%=3% | 85%*20%=17% |
所以应该是83%!!!!
好像很有道理啊有没有!
4.我觉得是用贝叶斯公式计算
设:A1表示”出租车是绿的”,A2表示“出租车是蓝的”,B表示“目击者认为是蓝车”
则:

答案大约是41.37%!
好像很有道理啊有没有!
看了几个帖子,网上也是争吵不休,也有些人讲第四种方法,说什么:
把题中目击者正确辨认概率改为0%,那么目击者的条件可以去除,那么正确答案就是蓝车自身概率15%!!但是用你这逻辑算出来是0%!
大家可以探讨一下... ...
为啥23的表可以这么乘。。。这样乘出来是在所有情况下确实是蓝车并且辨认为蓝车的概率,就算按第二个表的话也应该是取第一列0.12/(0.12+0.17)=0.43
1和4的分歧在于1中“正确辨认蓝车的概率”是辨认出蓝车的情况下确实是蓝车的概率,4中是确实是蓝车的情况下辨认为蓝车的概率。。
如果按4理解的话,若“正确辨认的概率”为0,那就是在任何情况下此人遇到蓝车就辨认为绿车,遇到绿车就辨认为蓝车,辨认到蓝车时确实是蓝车的概率自然是0.
/*刚才的方法有误,得到的是的是目击者看到蓝车的概率。现已更正。*/
我的方法是暴力统计。
题目中“该目击者可正确辨认车是蓝色的概率是80%,不能正确辩认的概率是20%。”一句,若理解成“目击者有80%概率正确辨认车的颜色”,则:
C++#include "pch.h"
#include "math.h"
#include "time.h"
#include <iostream>
int main()
{
long CarB = 0, CarG = 0, CarB_t = 0;
long count = 1000000;
double k1 = 0, k2 = 0, k = 0;
bool a = 0;
srand((int)time(0));
while (count--) {
if (rand() % 20 > 2) {//产生0-19的随机数,并判断
a = 0;//若为3-19,则为绿车
}else {
a = 1;//若为0-2,则为蓝车
CarB_t++;
}
if (rand() % 5 < 1) { 目击者20%概率误判 a =" ~a;" } if (a ="= 0) {" carg++; }else { carb++; k1 =" CarB_t;" k2 =" CarB;" k =" k1 / k2;" printf("green car(likely):%d\n", carg); printf("blue car(likely):%d\n", carb); printf("blue car(truth):%d\n", carb_t); printf("true blue car ratio="%f\n", k);" }< pre></ 1) {></iostream>运行结果:
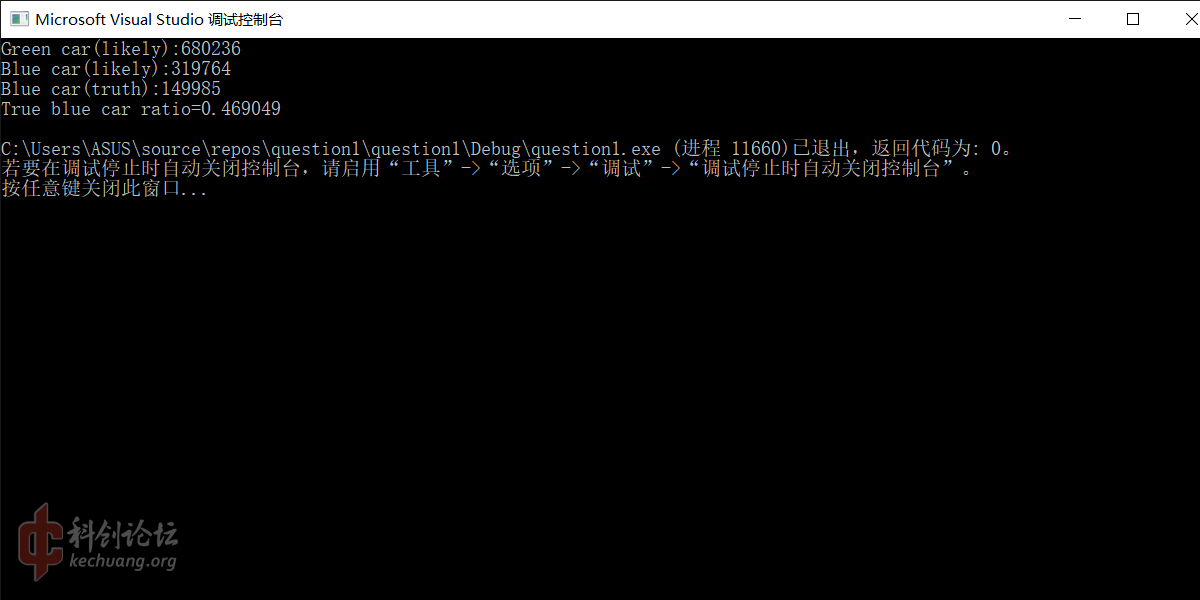
大约46.9%

 难道我又搞错了?
难道我又搞错了?
/*刚才的方法有误,得到的是的是目击者看到蓝车的概率。现已更正。*/我的方法是暴力统计。题目中“该目...
这个代码统计出来的似乎是目击者辨认出的蓝和绿色车的比例
/*刚才的方法有误,得到的是的是目击者看到蓝车的概率。现已更正。*/我的方法是暴力统计。题目中“该目...
改完之后的carb_t把实际上是蓝车但辨认为绿车的情况也算进去了
算法很有趣,错误也很经典。首先,需要将不能正确辩认理解为没看清的情况下说成是蓝车,实际可能是蓝或绿。
在出现概率计算可能存在错误的时候,我一般会采用列举实例验证条件的方法验证计算结果。
算法我就不重复了。我直接列举实例。
根据条件2,蓝:绿=3:17,不妨设实际数量,蓝车300,绿车1700辆。
再根据条件1和3,分为4组车,240:60:1360:340,则以240辆蓝车为目击为蓝车且确实正确辨认的数量。①
则,算法1的比例蓝/总应为 240:300,绿车60,则240为母鸡为蓝车,且确实是蓝车的数量,与①描述不符。
错误原因可以认为是,条件3中错误不能正确辩认理解为必为绿车。
算法2的比例蓝/总应为 240:1600,绿车为1360,则取到240的概率为任取一辆车是蓝车的概率,或描述为目击者完全无法分辨车辆颜色,与条件3不符。错误原因为算了看到是绿车的情况,与条件1不符。
算法3的比例蓝/总为(240+60*3/20):300,绿车为51,与所有条件均不矛盾。
算法4的比例蓝/总为240:580,绿车为340,这个描述起来很难,240为目击者确实会正确辨认的蓝车总数量,340为目击者确实会辨认错误的绿车总数量,取样范围均为2000辆汽车的总数量。可以看出是错误的,因为未包含没看清的情况下蓝车的情况。
楼主的编程算法比例为(240+60):640,绿车为340,与算法4一致,240为目击者确实会正确辨认的蓝车总数量,60为目击者无法辨别的蓝车总数量,340为目击者确实会辨认错误的绿车总数量,取样范围均为2000辆汽车的总数量。似乎是正确的,但出错的原因在于这种算法相当于让目击者目击每一辆出租车肇事情形(太残忍了),然后统计蓝绿数量和蓝绿比例,而其实这种方式下蓝绿车的基本情形的概率不同。
我们可以极限地想一下,仅有一辆蓝车,目击者认为有99%的把握认清是蓝车,而绿车有100000000万辆,你不会告诉我大概率是不是蓝车吧?
我其实还有算法5,不能认清,则非蓝即绿,这个概率应为各占50%,而非3:17,因为目击者只目睹了一辆车,跟车辆实际比例没有任何关系,则是蓝车的概率应为80%+20%*50%=90%,我个人比较推崇这个答案,虽然正确答案大概率不是这个。
我觉得楼上说的哪个极限例子是对于说法1的支持。
因为这个问题好像有点故意混淆概念了。
那我也举个例子,换个说法吧。
现在屏幕上有10*10的,100个像素点,都显示蓝色或者绿色,只有这两种颜色。
我都能看清,但是假设我有轻微色盲,有个医生要让我去辨认像素点颜色是否为蓝色,我正确辨认蓝色的概率是80%,但是我正确辨认绿色的概率不知道。
现在医生给我个画面,屏幕上只有一个点是蓝色,其它都是绿色。
题目1:请问这时候我正确找到蓝色点的概率是多少?
现在医生又给我一个画面,屏幕中有15%的像素点是蓝色,85%的点是绿色。
题目2来了:请问这时候我完全找出,或者辨认出15%的像素点的位置并且都正确的概率是多少?
然后医生给了一个奇怪的画面,屏幕中间区域有一个点可能是蓝色的,而其它蓝色点都在边缘上,隔离的很开。
题目3:请问这时候我判断正确,或者说辨认出中间区域的那个蓝色点的概率是多少?
从这个例子看,我确认了心中一直以来的疑惑。就是看没看错颜色,和车的总数量是没有关系的,看起来像是样本空间不重合的样子。
当然这也是我的个人看法。如果一定要已知在某种车辆颜色在城市所有车辆总数中所占的比例的条件下,问分辨的正确的概率,这似乎是符合条件概率的假设的。
嗯,但总有点那么,像是故意狗官诱导你招供的感觉。
情景翻译一下:
你:“我记不太清那天的情况了,我的判断有80%的概率是正确的。”
狗官一脸阴恻又问:”这个城市有99%的车都是绿色的,只有1%的车是蓝色的,你还确定你那天看到的是正确的嘛?“
你:“我,我不太确定了。”(贝叶斯公式可以作怪了,你心里对自己判断正确的概率的评估其实发生了变化)
看吧,想搞混一个人的脑子有时候也挺简单。
狗官还问:“你那天吃早饭了嘛?”
你:“没吃”
狗官说:“没吃早餐容易眼花哦~”
你:“……”
200字以内,仅用于支线交流,主线讨论请采用回复功能。