第一部分,一些基本概念:
在高中阶段(相见选修三第二章),我们曾接触过如下的公式
pV=C(玻意耳定律)
V=CT(盖—吕萨克定律)
p=CT(查理定理)
显然,为了更好的把ρ、p、T、V等物理量联系起来,上述公式无能为力,所以我们需要一个包含上述物理量的公式:
完全气体状态方程:
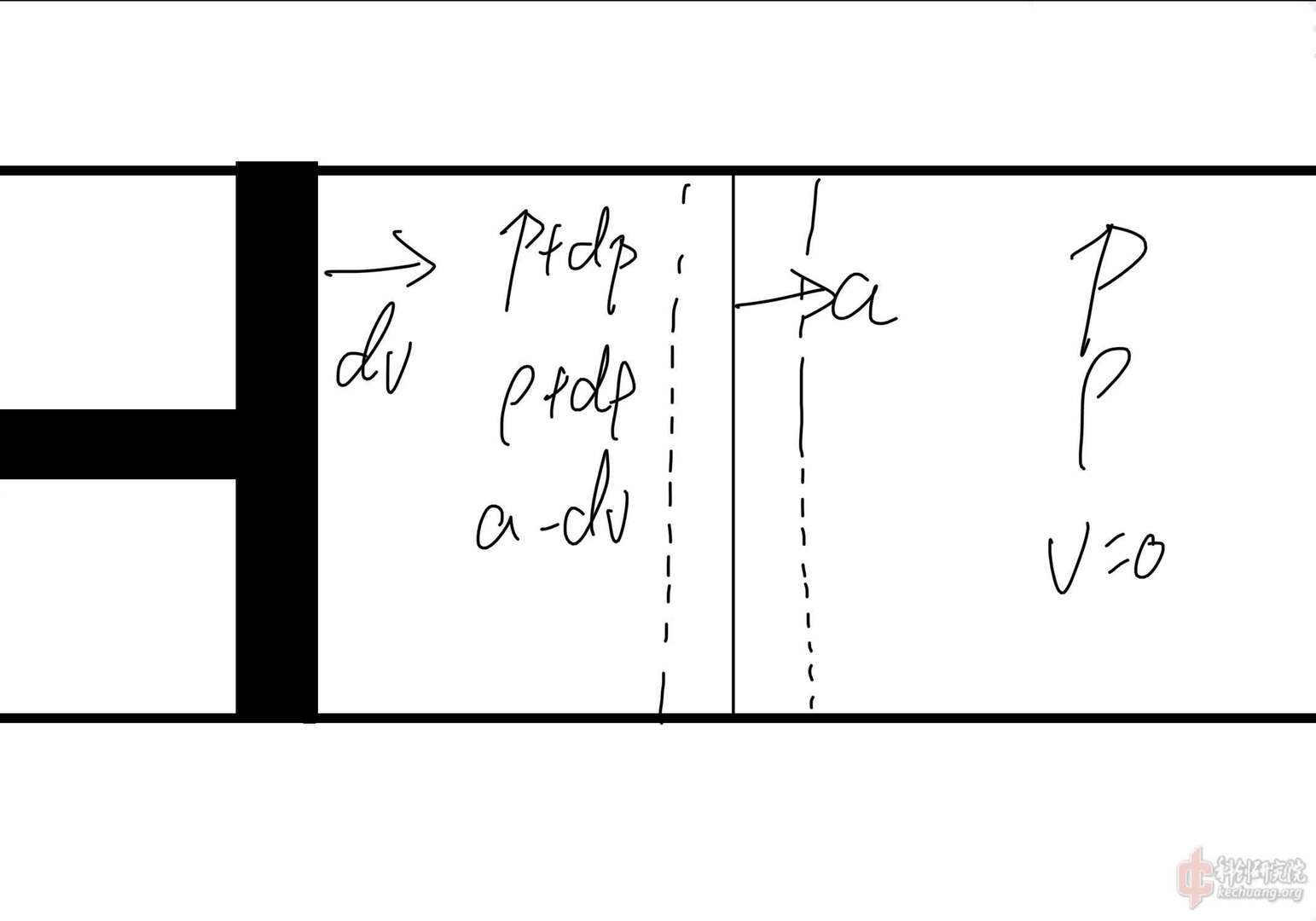
$p/ρ=RT$(式1-1)
其中:
R为气体常数,标准状况下:R=8314/M(J/kg•K),M为分子量。
需要注意,气体在低温高压,临近液化时,不再适用于上述公式。
我们把一个在与环境无热交换发生,且没有能量损耗的过程称为“等熵过程”
对于一个等熵过程,有:
$p/ρ^k=c$(式1-2)
如果不能理解这些公式的由来,可以作为定律使用,现阶段不必深究


200字以内,仅用于支线交流,主线讨论请采用回复功能。