【纸上谈兵】关于火箭喷管的一些基本理论 - 科创网

~~空空如也

加载中

加载中

鼓励

加载中...

加载中...

1年7个月前修改于 1年7个月前 IP:湖北

操作

发表于《【纸上谈兵】关于火箭喷管的一些基本理论》

第二部分，可压缩气流的一些基本定量关系：

取一根无限长，面积为A，内有压强为p，密度为ρ的可压缩流体的管道，左端有一活塞，以微小速度dv向右运动，如图2-1所示

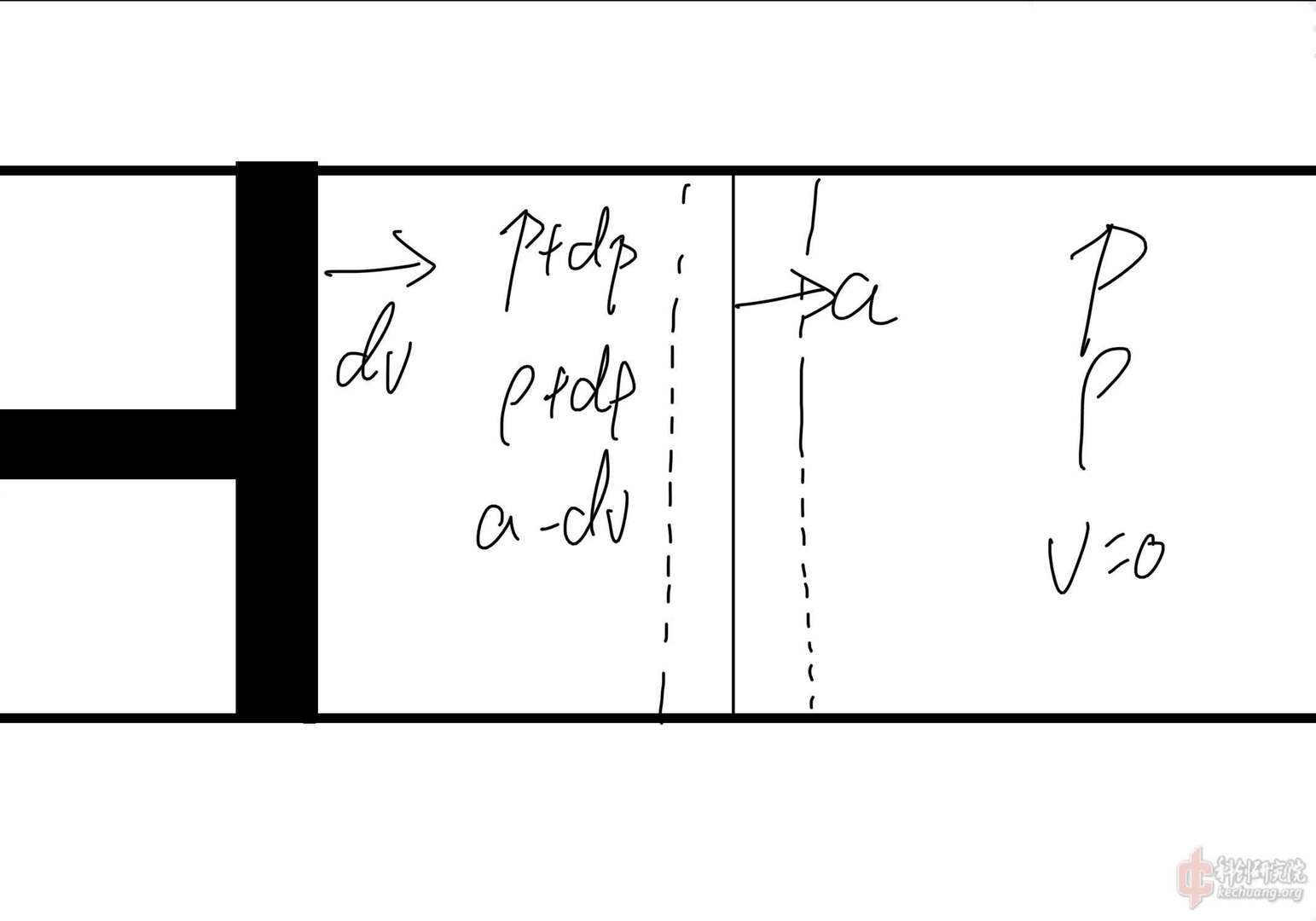
受由活塞运动所产生的速度为a的扰动波的影响，流体的压强、密度、速度均发生微小改变，分别变为p+dp、ρ+dρ、a-dv。

取活塞两侧虚线内区域为研究对象（即控制体），令控制体两面无限接近，故控制体体积趋近于零，得到控制体连续性方程和动量方程：

$ρ a A = (ρ + d ρ) (a - d v) A$

$p A - (p + d p) A = ρ a A [(a - d v) - a)]$

展开上二式，略去高阶微小项-dρdv，整理可得：

$a d ρ = ρ d v$

$ρ a d v = d p$

显然，由上二式可得：

$d v = d p / ρ a$

代入一式：

$a d ρ - d p / a = 0$

化简可得：

$a^{2} = d p / d ρ$ （式2-1）

由式（1-2）微分可得

$d p / d ρ =$ ckρ^k-1=kp/ρ（式2-2）

将式2-2和式1-2代入式2-1中可得：

$a^{2} = k p / ρ = k R T$

回复

粥粥回评

1年7个月前 IP:湖北

发现kc的公式编辑器不太好用，这里的多项式指数和分数都调不出来

虎哥回评

1年5个月前 IP:四川

用mathtype写好后，复制粘贴到编辑器中，可能需要设置mathtype的复制格式为latex。或者直接用latex代码写。

粥粥评论虎哥回评

1年5个月前 IP:湖北

ok

游客没有发表内容的权限。想参与大家的讨论？现在就登录或注册。

文号 / 925048

粥粥

百炼成钢

名片发私信
学术分 0
总主题 34 帖总回复 843 楼拥有证书：进士机友
注册于 2021-03-13 16:25最后登录 2025-04-04 12:34

主体类型：个人

所属领域：无

认证方式：手机号

IP归属地：湖北

个人简介

化工爱好者、数学物理小有涉猎

文件下载

加载中...

视频暂不能访问，请登录试试

仅供内部学术交流或培训使用，请先保存到本地。本内容不代表科创观点，未经原作者同意，请勿转载。

预览

音频暂不能访问，请登录试试

投诉或举报

加载中...

{{tip}}

请选择违规类型：

{{reason.type}}

空空如也

提交成功！

插入资源

全部

图片

视频

音频

附件

全部

未使用

已使用

正在上传

{{b.num+1}}{{b.num+1}}..

跳转到确定

空空如也~

上传中..{{f.progress}}%

处理中..

上传失败，点击重试

等待中...

{{f.name}}

空空如也~

(视频){{r.oname}}

{{selectedResourcesId.indexOf(r.rid) + 1}}

处理中..

处理失败

插入表情

我的表情

共享表情

Emoji

上传

{{b.num+1}}{{b.num+1}}..

跳转到确定

分享

注意事项

最大尺寸100px，超过会被压缩。为保证效果，建议上传前自行处理。
建议上传自己DIY的表情，严禁上传侵权内容。

点击重试等待上传{{s.progress}}%处理中...已上传，正在处理中

空空如也~

处理中...

处理失败

加载中...

草稿箱

加载中...

此处只插入正文，如果要使用草稿中的其余内容，请点击继续创作。

刷新{{b.num+1}}{{b.num+1}}..

{{fromNow(d.toc)}}

{{getDraftInfo(d)}}

标题：{{d.t}}

内容：{{d.c}}

继续创作

删除插入插入

插入公式

温馨提示

1. 公式行内显示(inline)：请使用 $....$ 或 \(....\) 包裹代码

2. 公式独占一行显示(display)：请使用 $$....$$ 或 \[....\] 包裹代码

3. 插入的公式在编辑时不会渲染，请检查无误后再插入。

公式输入

公式预览

\sum_{i = 0}^{N} \int_{a}^{b} g (t, i) d t

评论控制

加载中...

文号：{{pid}}

可查看、可评论

只可查看

不可查看、不可评论

笔记

{{note.content}}

{{n.user.username}}

{{fromNow(n.toc)}} {{n.status === noteStatus.disabled ? "已屏蔽" : ""}} {{n.status === noteStatus.unknown ? "正在审核" : ""}} {{n.status === noteStatus.deleted ? '已删除' : ''}}

编辑
删除
{{n.status === 'disabled' ? "解除屏蔽" : "屏蔽" }}

我也是有底线的