引用 QQQQQQQ:
第一张图不够准确,谐振子模型实际上是一种简化了的分子震荡模型,目的是方便计算,二次函数的抛物线实际上是在描述震荡的大体范围,通常情况下,无论是写成概率波的p 还是写成震荡分布波,很难超越这个二次函数……
简谐振子确实是一个非常理想化的模型,实际双原子分子的振动也偏离简谐振动。
其实我是考虑过以后将势能项改为Morse势能,再尝试数值求解的问题。
至于变分法,那更是要等以后才能have a try233333
现在在自学赖文的量子化学,最近看到简谐振子这一部分。书中以简谐振子为例,介绍了使用Numerov方法数值求解Schroedinger方程的方法,并提供了一个C++的代码来实现。因为我不会C++,所以就使用正在学的Python来尝试写一个(刚学到函数)。
我在维基上搜了一下,Numerov方法不只用于量子力学。但是涉及的其他的领域我不了解,所以无法介绍。总之就是单纯的讲讲求解一维谐振子波函数的方法。
一维量子谐振子的Schroedinger方程:
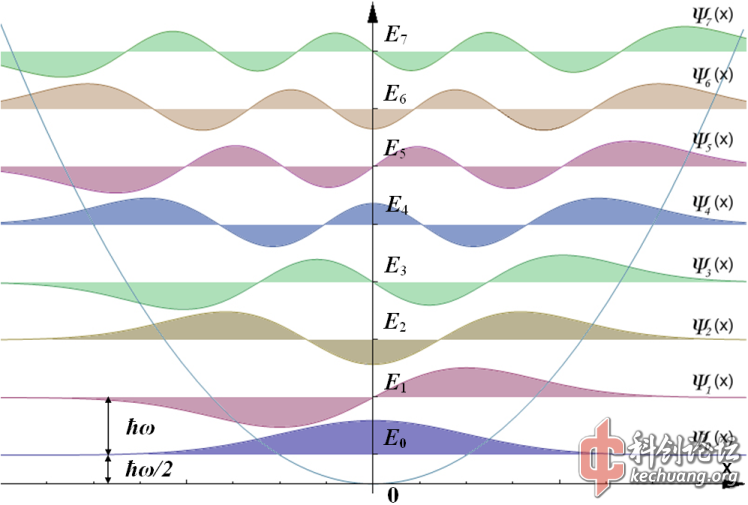
一维谐振子的解析解的求解不算很难,这里也不做介绍了。
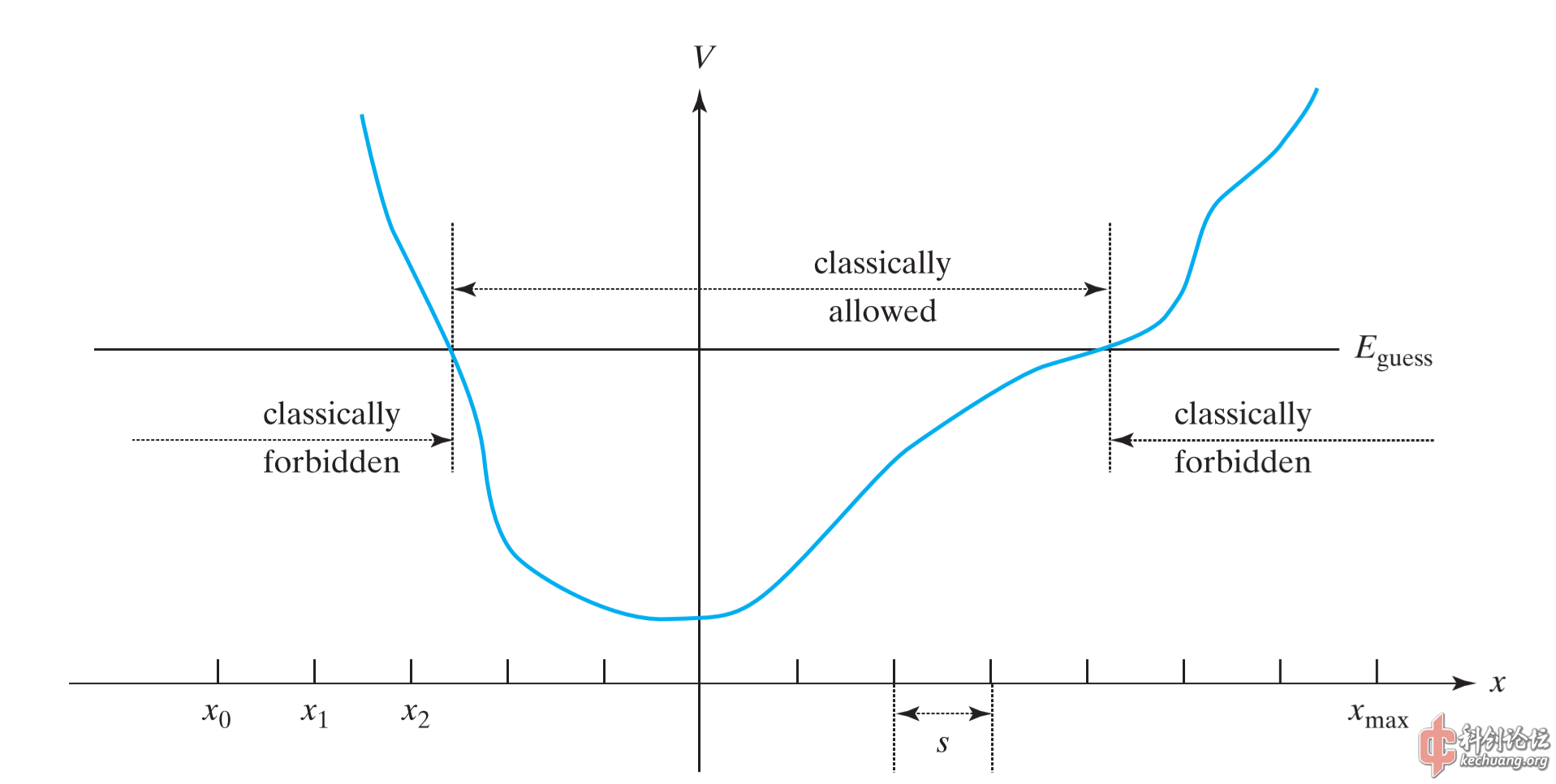
Numerov方法是基于递推,将我们所探讨的区域划分为多个小的间隔
将Schroedinger方程写为:
把
将两式相加(忽略后面的项):
用
忽略含6阶导的项:
将上式代入之前的式子,并代入
所以:
由此我们得到了该递推关系式。为了用该式求得波函数,我们首先需要得到
要进行递推,显然我们还需要猜测一个本征能量值
有了上述的方法,我们尝试用程序进行实现。
为了方便地进行计算,首先我们要做的一件事是将前面涉及的式子去量纲化(更准确的说法是将其转换为自然单位制)。
具体的变换不写了,并不算难。最终变换得到的Schroedinger方程为:
上式中:
经过处理,这些式子中的各个量的量纲均为1。
然后就是代码实现了。
(瞎画了一个流程图)

然后是python代码:
OtherX={"x0":0.0}
P={"p0":0.0}
G={"g0":0.0}
nn=0
x=float(input("Enter initial xr:"))
s=float(input("Enter the increment sr:"))
m=int(input("Enter the number of intervals m:"))
E=float(input("Enter the reduced energy Er:"))
for i in list(range(m+1)):
X["x%s" % i]=0.0 #储存x
for i in list(range(m+1)):
P["p%s" % i]=0.0 #储存psi
for i in list(range(m+1)):
G["g%s" % i]=0.0 #储存g
P["p1"]=0.0001
X["x0"]=x
X["x1"]=X["x0"]+s
G["g0"]=X["x0"]*X["x0"]-2*E
G["g1"]=X["x1"]*X["x1"]-2*E
ss=s*s/12
for i in range(1,m+1):
X["x%s" % (i+1)]=X["x%s" % i]+s
G["g%s" % (i+1)]=X["x%s" % (i+1)]*X["x%s" % (i+1)]-2*E
P["p%s" % (i+1)]=(-P["p%s" % (i-1)]+2*P["p%s" % i]+10*G["g%s" % i]*P["p%s" % i]*ss+G["g%s" % (i-1)]*P["p%s" % (i-1)]*ss)/(1-G["g%s" % (i+1)]*ss)
if (P["p%s" % i]*P["p%s" % (i+1)]<0): nn="nn+1" print("er="+str(E))
print(" nodes="+str(nn))
for i in range(m+1):
print(" psir(%f)="%f"" % (x["x%s" i],p["p%s" i])) < code></0):>
这个代码实际上写的很拙劣,因为我目前只学了一点,各位不要嘲笑……
关于输入的一点说明:为了让得到的结果尽可能精确,
运行该代码,写入输入,则得到输出(同时会计算节点的数量)。
OtherEnter initial xr:-4
Enter the increment sr:0.05
Enter the number of intervals m:160
Enter the reduced energy Er:0.5
Er=0.5
Nodes=0
Psir(-4.000000)=0.000000
Psir(-3.950000)=0.000100
Psir(-3.900000)=0.000204
Psir(-3.850000)=0.000315
...
其中最后一行为
OtherPsir(4.000000)=0.000489
可以看出,与0很接近。
若其偏离0,则需要手动对能量进行修改再次进行计算。
用以上数据在Origin中绘图:

与量子谐振子基态的波函数非常吻合(输出中表明了节点数为0)。
若修改初猜能量,得到第一激发态的波函数也是同样可行的。
但需要注意的一点是,当振动量子数为奇数时,P["p1"]=0.0001为-0.0001。
P.S.书中提供了一段C++实现代码:
实际使用代码尝试后会发现
这是非常理所当然的一点,因为量子谐振子的能级满足:
约化后能量自然等于0.5,1.5,2.5...
(以下内容我也不知道算不算画蛇添足)
所以我考虑通过修改代码,通过输入振动量子数,再利用程序自动对能量进行调整(由于程序原因,输入精确本征值,最后一点的波函数仍不够趋于0),最后进行数值计算。
所以我在进行最终计算前,设定一收敛条件,若
修改后的代码如下(同求不嘲笑……):
OtherX={"x0":0.0}
P={"p0":0.0}
G={"g0":0.0}
nn=0
x=float(input("Enter initial xr:"))
s=float(input("Enter the increment sr:"))
m=int(input("Enter the number of intervals m:"))
v=float(input("Enter the vibration quantum number:"))
if v%2==0:
P["p1"]=0.0001
else:
P["p1"]=-0.0001
p1=P["p1"]
E=v+0.5
El=v
Eh=v+1
M=E
#定义函数求最后一点的psir
def iteration(E,x0,s,m,p1):
p0=0.0
x1=x0+s
x2=x1+s
ss=s*s/12
for i in range(m-1):
g0=x0*x0-2*E
g1=x1+x1-2*E
g2=x2*x2-2*E
p2=(-p0+2*p1+10*g1*p1*ss+g0*p0*ss)/(1-g2*ss)
x0=x0+s
x1=x1+s
x2=x2+s
p0=p1
p1=p2
m=m-1
return p2
#二分法
while abs(iteration(E,x,s,m,p1))>0.0001:
if iteration(E,x,s,m,p1)>0:
if iteration(Eh,x,s,m,p1)<0: e="(E+Eh)/2" if iteration(e,x,s,m,p1)>0:
pass
else:
Eh=E
E=M
else:
E=(E+El)/2
if iteration(E,x,s,m,p1)>0:
pass
else:
El=E
E=M
else:
if iteration(Eh,x,s,m,p1)<0: e="(E+El)/2" if iteration(e,x,s,m,p1)<0: pass else: el="E" eh="E" x["x0"]="x" x["x1"]="X["x0"]+s" g["g0"]="X["x0"]*X["x0"]-2*E" g["g1"]="X["x1"]*X["x1"]-2*E" ss="s*s/12" for i in range(1,m): x["x%s" % (i+1)]="X["x%s"" i]+s g["g%s" (i+1)]*x["x%s" (i+1)]-2*e p["p%s" (i-1)]+2*p["p%s" i]+10*g["g%s" i]*p["p%s" i]*ss+g["g%s" (i-1)]*p["p%s" (i-1)]*ss) (1-g["g%s" (i+1)]*ss) (p["p%s" (i+1)]<0): nn="nn+1" print("er="+str(E))
print(" nodes="+str(nn))
for i in range(m+1):
print(" psir(%f)="%f"" (x["x%s" i],p["p%s" i])) < code></0:></0:>
在上面的代码中,我定义了一个函数用于求
从原理上来说,这段代码应该没有明显的毛病。但是发现得到的能量并不准确。
测试后发现是因为函数的输出与第一段代码的输出有明显的差距。
把函数的代码单独运行,并使其输出每一次得到的
Other0.0000000000
0.0001000000
0.00019873416928030692
0.00029497854356514764
0.00038754990743566356
0.00047532063060121913
0.0005572325408706247
0.0006323096548955608
0.0006996696081080572
...
0.26353345349798035
0.3024049078455913
0.3474895062785628
这是第一段代码的输出:
OtherPsir(-4.000000)=0.000000
Psir(-3.950000)=0.000100
Psir(-3.900000)=0.000204
Psir(-3.850000)=0.000315
Psir(-3.800000)=0.000436
Psir(-3.750000)=0.000573
Psir(-3.700000)=0.000728
...
Psir(3.900000)=0.000542
Psir(3.950000)=0.000506
Psir(4.000000)=0.000489
可以看出两段代码的输出结果的相差程度越来越大,到了最后一行,结果已经相差近三个数量级。用该函数的结果来调整能量的优化自然难以得到准确的结果。
我仔细检查了函数的代码,自认为没有错误。所以怀疑是浮点数精度(计算和储存时的四舍五入)的原因。
所以目前第二段代码暂不用来计算。
[修改于 8年3个月前 - 2017/03/02 13:13:37]
引用 QQQQQQQ:
第一张图不够准确,谐振子模型实际上是一种简化了的分子震荡模型,目的是方便计算,二次函数的抛物线实际上是在描述震荡的大体范围,通常情况下,无论是写成概率波的p 还是写成震荡分布波,很难超越这个二次函数……
引用 qiuzheru:说得没错。(就连处理的问题本身都属于最简单的模型之一)
Numerov方法本身是一个解常微分方程的线性多步法,只要是缺一阶项的二阶常微分方程就可用。
看来这个算法的想法是猜出一个能量本征值,再用其尝试数值求解波函数,判断与边界条件的符合程度再调整猜测的能量……
200字以内,仅用于支线交流,主线讨论请采用回复功能。