本帖最后由 friedel 于 2013-11-30 19:14 编辑 首先说下这个帖子纯属科普性质,重点不在C/2012 S1彗星上,有问题的话欢迎大家指正~
我们看到,ISON彗星已经通过了近日点,根据相关的轨道数据其近日点的日彗距离应该是1.94477*10^6km。
现在大家都很关心ISON的彗核有没有嗝屁的问题,最近的天文观测结果也显示这颗彗星似乎真的不妙了。在官方给出结果之前,我们先来做一些简单的计算,看看我们的ISON眼下的的形势是否对其有利。
稍懂点天文学的同学都知道“洛希极限”这个概念:当大质量星体与其小质量(相对大质量星体可忽略不计)卫星距离近到一定程度时,引力潮汐作用就会倾向于使卫星解体。当两者间距离恰好等于洛希极限时,卫星自身的重力与大质量星体对其造成的潮汐力达到平衡。而当这个距离小于洛希极限时,卫星就会倾向于解体而成为大质量星体的一个环。它以首个计算这个极限的人爱德华·洛希命名。
那么问题来了,怎么计算洛希极限呢?针对这个问题,我们可以先做出两种假设
假设一:卫星为刚体且其所有物质全部由重力维系在一起,卫星及其所环绕的大质量星体(下简称“大星”)均为球体。

在这种情况下,我们考虑卫星表面的最接近大星的质元u,有两股力作用在u上:卫星的引力和大星的引力。基于卫星在大星引力场内自由降落,当达到洛希极限时这两股力相等。设大星质量为M,半径为R;卫星质量为m,半径为r
设FG为卫星作用在u上的引力,根据牛顿引力定律,
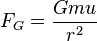
设d为卫星和大星中心的距离,FT为大星作用在u上的引力,则有
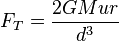
若卫星恰好在洛希极限,则有FG = FT,即
![ef11be64c827ea177a15511887530f75.png]()
提取d,化简得到
![96b209bed8cc21a89770953aff4af66c.png]()
,这里d的值就是两星体之间的洛希极限
又,M=(4*π*R^3*ρM[/size])/3,m=(4*π*r^3*ρm[/size])/3,
代入上式并化简,得到
![81081ddd0bc91fd3c1938905c3ca8be5.png]()
![a2263b8cda1335ff816c121a0fd59b29.png]()
以上就是卫星的“刚体洛希极限”计算公式的推导过程。
假设二:卫星为理想流体,其余条件不变。此时的卫星最容易解体。
由于流体卫星的洛希极限推导过程较为繁琐,这里不作推导(其实是lz数学不好吧魂淡)……
洛西给出的近似计算公式为
![b1b8fdbed48ac430ef64eedf86283774.png]()
借助计算机程序的帮助,较精确的解是
![7afbeeba7c5dbb88825a6fbf1a81b3d2.png]()
式中c / R是行星的扁度。
以上所做的两个假设是理想的两种情况,刚体卫星最不易解体而流体卫星最易解体。现实中的星体由于结构和组成物质的原因,其洛希极限通常在这两个数值之间。
OK我们来代入数字计算吧,太阳的平均密度是1.4*10^3kg/m^3,半径为6.955*10^5km;我们尚不知道ISON彗星的实际密度,此处取彗星的平均密度0.5*10^3kg/m^3
据此可以分别计算ISON彗星对太阳的刚体洛希极限为1.235*10^6km,流体洛希极限为2.392*10^6km(运用洛西给出的近似公式)。
再看ISON彗星近日点的日彗距离1.94477*10^6km,这个值正好落在两个洛希极限值之间大约61.3%接近流体洛希极限的位置上。鉴于彗星的彗核具有由岩石和冰构成的较为疏松的结构,其实际洛希极限会更接近流体洛希极限。这就意味ISON彗星在从近日点掠过太阳时,有相当大的可能会解体,更不用说太阳的巨大热量可能会把它直接蒸发了。
好吧看来我们的ISON局面不妙啊。。。嗯默哀片刻先……
不过呢,宇宙是不讲情面的,只是按照原理和定律一丝不苟地运行。重要的是,我们知道了洛希极限是怎么回事儿,这就足够了~

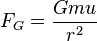
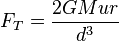
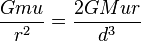
 ,这里d的值就是两星体之间的洛希极限
,这里d的值就是两星体之间的洛希极限




200字以内,仅用于支线交流,主线讨论请采用回复功能。