现在在自学赖文的量子化学，最近看到简谐振子这一部分。书中以简谐振子为例，介绍了使用Numerov方法数值求解Schroedinger方程的方法，并提供了一个C++的代码来实现。因为我不会C++，所以就使用正在学的Python来尝试写一个（刚学到函数）。

原理

我在维基上搜了一下，Numerov方法不只用于量子力学。但是涉及的其他的领域我不了解，所以无法介绍。总之就是单纯的讲讲求解一维谐振子波函数的方法。

$$ \hat{H}=\hat{T}+\hat{V}=-\frac{\hbar^2}{2m}\ \frac{d^2}{dx^2}+\frac{1}{2}\ kx^2=-\frac{\hbar^2}{2m}\ \frac{d^2}{dx^2}+2\pi^2\nu^2mx^2=-\frac{\hbar^2}{2m}\ (\frac{d^2}{dx^2}-\alpha^2x^2) $$ $$ \alpha=\frac{2\pi\nu m}{\hbar} $$

一维量子谐振子的Schroedinger方程： $$ \frac{d^2\psi}{dx^2}+(2mE\hbar^{-2}-\alpha^2 x^2)\psi=0 $$

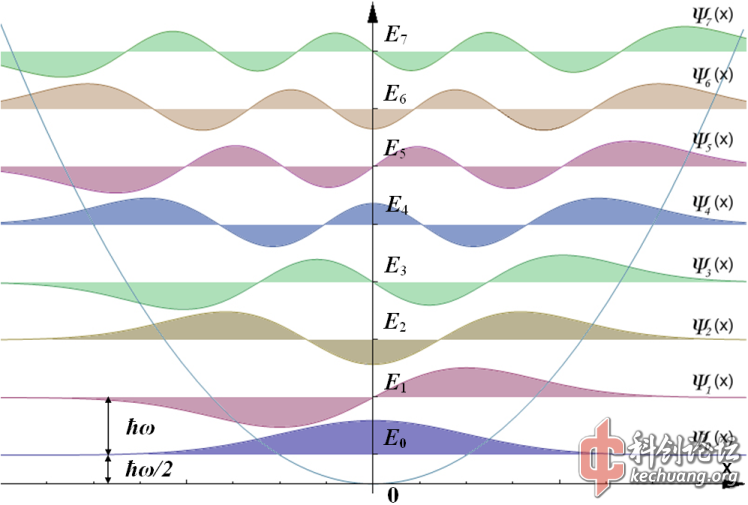
一维谐振子的解析解的求解不算很难，这里也不做介绍了。

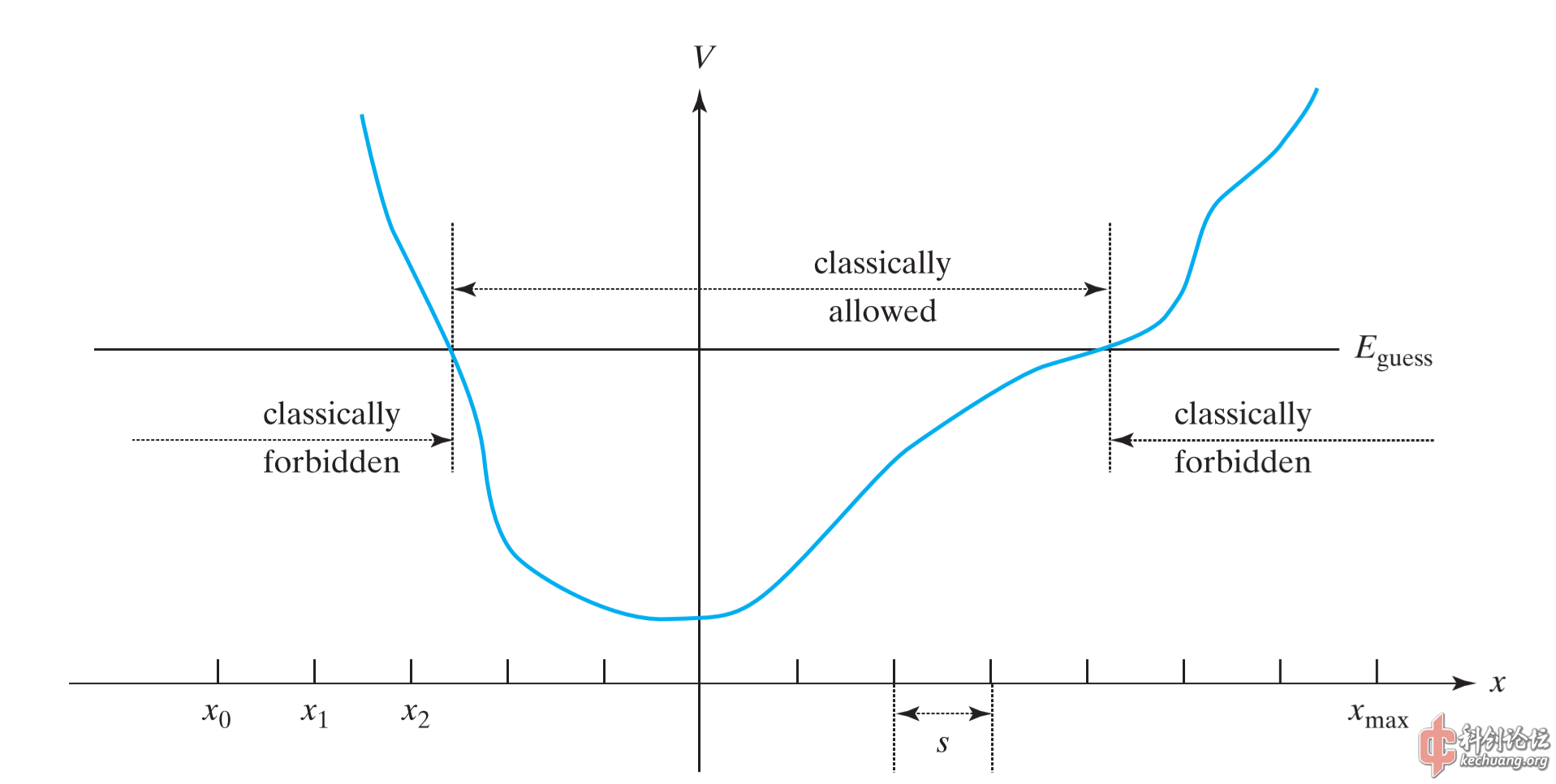
Numerov方法是基于递推，将我们所探讨的区域划分为多个小的间隔\(s\)。若我们取最左端的点的坐标为\(x_0\)，向右的点分别为\(x_1=x_0 +s,x_2=x_1 +s, \ldots ,x_\text{max} \)。设\(\psi_n, \psi_{n+1}, \psi_{n-1}\)分别表示\(\psi\)在\(x_n, x_n+s, x_n-s\)处的值：

$$ \psi(x_n)=\psi_n, \psi(x_n+s)=\psi_{n+1}, \psi(x_n-s)=\psi_{n-1} $$

将Schroedinger方程写为：

$$ \psi''=G\psi, G=m\hbar^{-2}[2V(x)-E] $$

把\(\psi(x_n+s)\)和\(\psi(x_n-s)\)进行Taylor展开：

$$ \psi(x_n+s)=\psi(n)+\psi'(n)\cdot s+\frac{\psi''(n)}{2}\cdot s^2+\frac{\psi'''(n)}{3!}\cdot s^3+\frac{\psi^\text{(4)}(n)}{4!}\cdot s^4+\frac{\psi^\text{(5)}(n)}{5!}\cdot s^5+\ldots $$

$$ \psi(x_n-s)=\psi(n)-\psi'(n)\cdot s+\frac{\psi''(n)}{2}\cdot s^2-\frac{\psi'''(n)}{3!}\cdot s^3+\frac{\psi^\text{(4)}(n)}{4!}\cdot s^4-\frac{\psi^\text{(5)}(n)}{5!}\cdot s^5+\ldots $$

将两式相加（忽略后面的项）：

$$ \psi_{n+1}=-\psi_{n-1}+2\psi_n+\psi''_n\cdot s^2+\frac{\psi^\text{(4)}_n}{12}\cdot s^2 $$

用\(\psi''\)代替\(\psi\)，并两边乘以\(s^2\)：

$$ \psi''_{n+1} \cdot s^2=-\psi''_{n-1}\cdot s^2+2\psi''_n\cdot s^2+\psi^\text{(4)}_n\cdot s^4+\frac{\psi^\text{(6)}_n}{12}\cdot s^6 $$

忽略含6阶导的项：

$$ \psi^\text{(4)}_n\cdot s^4=\psi''_{n+1}\cdot s^2+\psi''_{n-1}\cdot s^2-2\psi''_n\cdot s^2 $$

将上式代入之前的式子，并代入\(\psi''=G\psi\)：

$$ \psi_{n+1}=-\psi_{n-1}+2\psi_n+G_n\psi_n s^2+\frac{1}{12}\ [G_{n+1}\psi_{n+1}s^2+G_{n-1}\psi_{n-1}s^2-2G_n\psi_n s^2] $$

所以：

$$ \psi_{n+1}=\frac{2\psi_n-\psi_{n-1}+5G_n\psi_n s^2 /6+G_{n-1}\psi_{n-1}s^2 /12}{1-G_{n+1}s^2 /12} $$ $$ G_n=G(x_n)=m\hbar^{-2}[2V(x_n)-2E] $$

由此我们得到了该递推关系式。为了用该式求得波函数，我们首先需要得到\(\psi_0, \psi_1\)。 根据经典力学，\(E<V\)的区域为禁阻区域；而在量子力学中，由于隧穿效应，在\(E<V\)的区域，波函数\(\psi\)并不为零。但是进入经典禁阻区域越深，\(\psi\)越趋于零。因此我们假定\(\psi(x_0)=\psi_0=0\)。而对于\(x_1\)点，假设波函数在该点为一很小的值，比如可以取0.0001。事实上取0.001也是可以的，这相当于将波函数乘以10，通过归一化处理后并没有什么区别。

要进行递推，显然我们还需要猜测一个本征能量值\(E_\text{guess}\)。经过递推最终得到\(\psi(x_\text{max})\)。根据品优波函数平方可积或对称性的要求，\(\psi(x_\text{max})\)应当趋近于零。若\(\psi(x_\text{max})\)远远偏离0，说明我们猜测的能量本征值不够合理，需要重新进行猜测。

有了上述的方法，我们尝试用程序进行实现。

程序实现

为了方便地进行计算，首先我们要做的一件事是将前面涉及的式子去量纲化（更准确的说法是将其转换为自然单位制）。

具体的变换不写了，并不算难。最终变换得到的Schroedinger方程为： $$ \frac{d^2\psi_r}{dx^2_r}=(2V_r-2E_r)\psi_r $$

$$ \psi''_r=G_r \psi_r, G_r=2V_r-2E_r $$

上式中：\(V_r=\frac{1}{2}\ x_r^2\)。

经过处理，这些式子中的各个量的量纲均为1。

然后就是代码实现了。

（瞎画了一个流程图）

然后是python代码：

<code class="language-python">X={"x0":0.0}
P={"p0":0.0}
G={"g0":0.0}
nn=0

x=float(input("Enter initial xr:"))
s=float(input("Enter the increment sr:"))
m=int(input("Enter the number of intervals m:"))
E=float(input("Enter the reduced energy Er:"))

for i in list(range(m+1)):
	X["x%s" % i]=0.0 #储存x

for i in list(range(m+1)):
	P["p%s" % i]=0.0 #储存psi
	
for i in list(range(m+1)):
	G["g%s" % i]=0.0 #储存g

P["p1"]=0.0001
X["x0"]=x
X["x1"]=X["x0"]+s
G["g0"]=X["x0"]*X["x0"]-2*E
G["g1"]=X["x1"]*X["x1"]-2*E
ss=s*s/12

for i in range(1,m+1):
	X["x%s" % (i+1)]=X["x%s" % i]+s
	G["g%s" % (i+1)]=X["x%s" % (i+1)]*X["x%s" % (i+1)]-2*E
	P["p%s" % (i+1)]=(-P["p%s" % (i-1)]+2*P["p%s" % i]+10*G["g%s" % i]*P["p%s" % i]*ss+G["g%s" % (i-1)]*P["p%s" % (i-1)]*ss)/(1-G["g%s" % (i+1)]*ss)
	if (P["p%s" % i]*P["p%s" % (i+1)]<0): nn="nn+1" print("er="+str(E))
print(" nodes="+str(nn))
for i in range(m+1):
	print(" psir(%f)="%f"" % (x["x%s" i],p["p%s" i])) < code></0):></code>

这个代码实际上写的很拙劣，因为我目前只学了一点，各位不要嘲笑……

关于输入的一点说明：为了让得到的结果尽可能精确，\(s\)的选择应当尽量小一些，这样可以绘制更多的点。m为间隔的数量，显然\(m=\frac{(x_\text{max}-x_0)}{s}\)。

运行该代码，写入输入，则得到输出（同时会计算节点的数量）。

<code class="language-python">Enter initial xr:-4
Enter the increment sr:0.05
Enter the number of intervals m:160
Enter the reduced energy Er:0.5
Er=0.5
Nodes=0
Psir(-4.000000)=0.000000
Psir(-3.950000)=0.000100
Psir(-3.900000)=0.000204
Psir(-3.850000)=0.000315
...
</code>

其中最后一行为\(x_\text{max}\)的波函数值：

<code class="language-python">Psir(4.000000)=0.000489
</code>

可以看出，与0很接近。

若其偏离0，则需要手动对能量进行修改再次进行计算。

用以上数据在Origin中绘图：

与量子谐振子基态的波函数非常吻合（输出中表明了节点数为0）。

若修改初猜能量，得到第一激发态的波函数也是同样可行的。

但需要注意的一点是，当振动量子数为奇数时，\(\psi\)首先是小于零的。因此需要修改代码中的P["p1"]=0.0001为-0.0001。

P.S.书中提供了一段C++实现代码：
Numerov method.cpp 0.81KB CPP 77次下载

修改版代码

实际使用代码尝试后会发现\(E_0, E_1, E_2,\ldots\)分别近似等于0.5，1.5，2.5...（不是严格相等大概是程序计算时数值精度的原因）

这是非常理所当然的一点，因为量子谐振子的能级满足：

$$ E_v=(v+\frac{1}{2}\ )h\nu $$

约化后能量自然等于0.5，1.5，2.5...

（以下内容我也不知道算不算画蛇添足）

所以我考虑通过修改代码，通过输入振动量子数，再利用程序自动对能量进行调整（由于程序原因，输入精确本征值，最后一点的波函数仍不够趋于0），最后进行数值计算。

所以我在进行最终计算前，设定一收敛条件，若\(\psi(x_\text{max})\)的绝对值小于0.0001，则判断\(E_\text{guess}\)足够准确。并由此进行计算。

修改后的代码如下（同求不嘲笑……）：

<code class="language-python">X={"x0":0.0}
P={"p0":0.0}
G={"g0":0.0}
nn=0

x=float(input("Enter initial xr:"))
s=float(input("Enter the increment sr:"))
m=int(input("Enter the number of intervals m:"))
v=float(input("Enter the vibration quantum number:"))

if v%2==0:
        P["p1"]=0.0001
else:
        P["p1"]=-0.0001

p1=P["p1"]
E=v+0.5
El=v
Eh=v+1
M=E
#定义函数求最后一点的psir
def iteration(E,x0,s,m,p1):
        p0=0.0
        x1=x0+s
        x2=x1+s
        ss=s*s/12
        for i in range(m-1):
                g0=x0*x0-2*E
                g1=x1+x1-2*E
                g2=x2*x2-2*E
                p2=(-p0+2*p1+10*g1*p1*ss+g0*p0*ss)/(1-g2*ss)
                x0=x0+s
                x1=x1+s
                x2=x2+s
                p0=p1
                p1=p2
                m=m-1
        return p2
#二分法
while abs(iteration(E,x,s,m,p1))>0.0001:
        if iteration(E,x,s,m,p1)>0:
                if iteration(Eh,x,s,m,p1)<0: e="(E+Eh)/2" if iteration(e,x,s,m,p1)>0:
                                pass
                        else:
                                Eh=E
                                E=M
                else:
                        E=(E+El)/2
                        if iteration(E,x,s,m,p1)>0:
                                pass
                        else:
                                El=E
                                E=M
        else:
                if iteration(Eh,x,s,m,p1)<0: e="(E+El)/2" if iteration(e,x,s,m,p1)<0: pass else: el="E" eh="E" x["x0"]="x" x["x1"]="X["x0"]+s" g["g0"]="X["x0"]*X["x0"]-2*E" g["g1"]="X["x1"]*X["x1"]-2*E" ss="s*s/12" for i in range(1,m): x["x%s" % (i+1)]="X["x%s"" i]+s g["g%s" (i+1)]*x["x%s" (i+1)]-2*e p["p%s" (i-1)]+2*p["p%s" i]+10*g["g%s" i]*p["p%s" i]*ss+g["g%s" (i-1)]*p["p%s" (i-1)]*ss) (1-g["g%s" (i+1)]*ss) (p["p%s" (i+1)]<0): nn="nn+1" print("er="+str(E))
print(" nodes="+str(nn))
for i in range(m+1):
        print(" psir(%f)="%f"" (x["x%s" i],p["p%s" i])) < code></0:></0:></code>

在上面的代码中，我定义了一个函数用于求\(\psi(x_\text{max})\)，再利用二分法调整能量\(E\)，当\(\psi(x_\text{max})\)满足收敛条件后，便使用调整后的能量计算各点波函数的数值（这部分与第一段代码没有区别）。

从原理上来说，这段代码应该没有明显的毛病。但是发现得到的能量并不准确。

测试后发现是因为函数的输出与第一段代码的输出有明显的差距。

把函数的代码单独运行，并使其输出每一次得到的\(\psi\)（前两行是我手动补上去的）

<code class="language-python">0.0000000000
0.0001000000
0.00019873416928030692
0.00029497854356514764
0.00038754990743566356
0.00047532063060121913
0.0005572325408706247
0.0006323096548955608
0.0006996696081080572
...
0.26353345349798035
0.3024049078455913
0.3474895062785628
</code>

这是第一段代码的输出：

<code class="language-python">Psir(-4.000000)=0.000000
Psir(-3.950000)=0.000100
Psir(-3.900000)=0.000204
Psir(-3.850000)=0.000315
Psir(-3.800000)=0.000436
Psir(-3.750000)=0.000573
Psir(-3.700000)=0.000728
...
Psir(3.900000)=0.000542
Psir(3.950000)=0.000506
Psir(4.000000)=0.000489
</code>

可以看出两段代码的输出结果的相差程度越来越大，到了最后一行，结果已经相差近三个数量级。用该函数的结果来调整能量的优化自然难以得到准确的结果。

我仔细检查了函数的代码，自认为没有错误。所以怀疑是浮点数精度（计算和储存时的四舍五入）的原因。

所以目前第二段代码暂不用来计算。