牛顿的经典力学的创立使得1666年成为了物理学世上的一个奇迹年，而爱因斯坦于1905年发表了质能公式是1905年成为了继牛顿之后的又一个奇迹年。

    齐奥尔科夫斯基方程是基于牛顿的的经典力学推导出来的，在经典力学中速度没有上限，任何参考系下的变换为伽利略变换，

即                                        

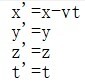
   但是随着理论和实验相继反映出在任何运动参考系下光速不变，洛伦兹变换作为修正被提出

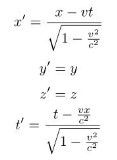
因此齐奥尔科夫斯基方程也会有一个相对论的修正，就是阿克莱方程。值得注意的是在低速运动的情况下齐奥尔科夫斯基方程和阿克莱方程非常接近，所以用齐奥尔科夫斯基方程可在一定情况下简化计算。

           先了解一下相对论的速度变换，设A B C 三个小球

这里是以A为参考系（设A不动）B C分别以-v和u的速度远离A,u可视为航天器的喷气速度。值得注意的是这里的M和m是物体的动质量，其与静质量m0的关系为m=m0/γ  (γ=√(1-v²/c²)

以B为参考系则有

在相对论中的速度变换并不是简单的叠加以情景为例：当以B为参考系时       

   u=(v+u')/(1+vu'/c²)     以A为参考系时   u'=(-v+u)/(1-vu/c²)   

根据动量守恒定理可知在以B为参考系的情况下      (M-m)v+mu'=0

可写成                   (M0-m0)v*f(v)+m0u'*f(u')=0   f(x)=1/(√1-x² /c² )         

这时有两种想法来推导(第二种是未经总结和验证）

1. 钱老在《星际航行概论》中的方法

         将动量守恒改写成微分方程的形式
   

因为书中对各个字母和符号的设置不同所以付加其设定

后通过一通操作后   

最后凑出了一个整洁的等式（一个火箭质量增量和其速度与光速之比的增量的反函数）

对其积分得阿克莱方程

        化简得  (M⁽¹⁾ /M⁽²⁾ )^2w/c =(c+v)/(c-v)     

 将(M⁽¹⁾ /M⁽²⁾ )^2w/c 设为Q                  最终化简得Dv=c(Q-1)/(Q+1)

(2)第二种方法,设想C是航天器A以速度u往后喷射的推进剂，其动质量为m,假设每一个m和dv（速度的增量）之间有联系为

dv=g(m)*dm      

将动量守恒方程化为    (M0-dm0)*dv*f(v+dv)+dm0*u'*f(u')=0    然后又是一通操作把其转化为

dv/dm0=h(m0)或dm0/dv=h^-1 (m0)的形式后对其进行不定积分   H(m0)=∫h(m燃0)dm0  因为m0=0是Dv(速度的增量)=0

所以Dv=H(m燃0)=∫h(m燃0)dm0              其中m燃0为燃料静止时的总质量

              省略的一通操作很复杂，其主要原因是u'是一个带着v的函数，且u'还有二次

     可能会有有错误的或不规范的地方，请大家指正，希望能多多交流。

      今天年三十了，提前祝大家新年快乐！！！