对比boost效率高,主要得益于薄膜电容内阻低,但也有另一个因素,就是与脉宽和线圈有关。线圈电感量虽然更低了,但是也更短了,以致于时间常数τ=L/R不变或者高一些,脉宽也更小,即半波的角频率ω增高,线圈的品质因素Q=ωL/R=ωτ也增加(导致内阻损耗的比例更低)。
另外,是不是也因与波形有关,比boost更贴近正弦半波而引起的效率上涨,暂时没法下定论。
PS:经典薄膜磁阻暂时还没有传统薄膜磁阻的说法。在这之前圈内极为罕见的形式。
经典的薄膜谐振关断拓扑中,电压因放电是震荡衰减的,一个电容存储的能量只够两三级进行释放,这就需要通过增加电容个数来增加级数。由于薄膜电容较低的能量密度,体积也会同时增加。@rb-sama提出使用全桥谐振电路在放电时进行补偿。但这个拓扑有着一些设计难点,如薄膜电压易超压,补偿电容csum难确定取值的问题,我自己也进行了仿真测试,在较大的csum下无法良好控制输入的能量,导致中间级放掉了很多能量。
考虑只在一半级数中进行补偿或许能得到较好的效果并降低设计难度。于是我基于buck电路设计了一种新的电炮拓扑结构,可以在奇数级发射时对薄膜电容进行补偿,结构如图所示:
![4F91@{YV]1CH}U3X{OSXT[O.png](https://img.kechuang.org:81/r/335673?c=resource)
它的基础构型由一个大容量电容C1,小容量薄膜电容C2,控制能量输入的igbt开关Q1,续流二极管D0(不需要调功可将Q1换为SCR并删除D0),以及可控硅组D1-Dx控制线圈导通。
![QX60MU($7V_{B{D~]~JUO$H.png](https://img.kechuang.org:81/r/335674?c=resource)
工作主要过程分为奇数级和偶数级两种状态,假设不预充电即C2初始电压为0;
开始时第一级工作,Q1,D1同时导通,C1提供能量给L1并同时对C2充电,C2电压上升,同时L1上产生磁场加速弹丸。该回路可等效为RLC串联回路,由于其中存在可控硅,电流过零关断。
偶数级工作时D(2N)导通,此时就是经典的薄膜磁阻工作过程,C2对L(2N)进行放电。同样RLC串联回路过零关断。C2电压由上正下负变为上负下正。
当奇数级开启,Q1,D(2N+1)开通,C2和C1同时对L(2N+1)放电。C1在这个过程中对C2进行补偿,放电后C2电压再次变为上正下负,若在该过程中若C2电压将超过耐压,可提前关断Q1,电流将经过D0进行续流。
以上是该拓扑工作过程,该拓扑的性能与薄膜磁阻无异,并且得益于薄膜电容的低内阻,即使在单级小容量场合下也有着极低的内阻损耗。在控制逻辑上该拓扑也是相当简单的,可完全使用光电驱动。
不难看出当C2容量是确定的时候每级的输入几乎完全取决于C2的电压,而这个拓扑能为薄膜补偿多少能量是我们主要关心的内容,因此C2的电压将是本文分析的一个重点。

在奇数级的放电回路如上所示,该回路可简化为RLC电路如下,可看成C1C2串联成一个新的C,电压为C1与C2的串联电压。

可以用下述二阶齐次微分方程描述,其中C是C1和C2串联等效后的电容量:
![RIL53Y`{$RTQB@8UAQ)}]FT.png](https://img.kechuang.org:81/r/335681?c=resource)
省略求特征方程和特征根带入电容电压响应初始值等过程
令


则可表示为:

最终求解得电压响应为:
![[)`PL]WS9~0@1XB`TYA}IFV.png](https://img.kechuang.org:81/r/335690?c=resource)
电流响应为:
![BZU3@M_16TQTA]2XUH$D47Q.png](https://img.kechuang.org:81/r/335691?c=resource)
电流为零时间即为谐振关断时间:

电流过零关断时的等效电容的电压为:

由于回路电流处处相等,则有

则C1C2两端的电压变化量与容量成反比

由电容电压等于串联电压和可得
![~R(R4~6[JJUQME]ZE5SR3~J.png](https://img.kechuang.org:81/r/335711?c=resource)
解得各电容放电前后的电压差值


得到奇数级放电后电容U2的电压

![N9}M7XG)VBHJM`TX_{D]Z_9.png](https://img.kechuang.org:81/r/335716?c=resource)
可以看到奇数级放电后的电压与电容C1C2的容量、C1C2串联等效电容电流过零关断时电压Ux、C1的初始电压U0、C2初始电压U2初这几个参数有关,其中不难看出C1/C2和U0的值越大,放电后的电压越高,在偶数级就能输入更多能量。
但其中C1C2串联等效电容在过零关断时电压Ux相关的参数较多,不容易直接确定哪些参数会有直接影响。
因此这里使用线性系统时域方法分析,可将这个RLC电路看成欠阻尼二阶系统的零输入响应。
当这个系统电容两端电压到达最低谷时,电压对时间的导数为0,此时电流过零关断。可将这一过程看作一个反向的阶跃响应。因此只要计算出这个二阶系统的在阶跃响应的超调量就可以知道电容过零关断时的电压。
其中该RLC电路形成的二阶系统的阻尼比是:

根据二阶系统特征参数公式可直接计算出超调量:

无论阻尼比的取值超调量始终小于1,因此假设C1>>C2忽略电阻以及其他能量损失,在第一次放电后C1+C2的串联电压为-U0,由于C1仍为U0,U2电压为2U0。第三次放电后U2两端电压为4U0。 第五次放电后U2两端电压为6U0。 则第2n+1次放电后U2两端电压绝对值为2n+2倍U0。可以看出增加的其实是2倍C1上的电压,并且每次补偿的能量随着C2电压绝对值增加而增加。在实际工程中,可以找到每两级消耗和补偿的一个平衡点来确定C2的工作电压。
现在考虑如何使电容电流过零关断时电压Ux更大,结果就显而易见了,即应当使得阻尼比的值越小,C2在补偿后电压是越高的。
![}[BF]N~G~3I3M80_`~RE957.png](https://img.kechuang.org:81/r/335720?c=resource)
Q即是RLC串联电路中的品质因数,提高品质因数便能提高电压,由于C的品质是厂家决定的,最直接的办法就是降低走线电阻和提高制作线圈的工艺水平。
对以上两种计算方法带入一组值进行验证,假设C1=2310uf,C2=110uf,L=200uH,R=0.5Ω,U0=400V,U2初=0V,则C1与C2串联后的C=105uf
方法1计算Ux:

方法2计算Ux:阻尼比e=0.181142 超调量%=56.0656% U(i=0)=-400*0.560656=-224.262V
![VW_{Y]U{QCJUPO(YZN~F]GN.png](https://img.kechuang.org:81/r/335722?c=resource)
根据上面计算的公式得到补偿后的C2两端电压:

U2末=-2310*(-224.2624-400+0)/(2310+110)=595.886v

和在multisim中得到的仿真结果一致,在这个过程中是忽略了磁场能量的损失、开关压降和电阻损耗,所以利用上述公式计算出的实际电压会小于该值。
根据以上理论的结果进行设计并在maxwell进行有限元仿真:
设计的C1电压400V容量5000uf,C2容量110uf,单级线圈长12mm,两级间隔1mm,共15级加速,总长195mm。发射口径12mm长度22mm19.3g的圆柱销。这样使用较短的线圈会导致在加速时至少有连续的两级同时工作,因此电路分三路工作以达到紧密连续加速的效果。而紧密加速能有效提高效率,减少电阻以及涡流损耗,这里对其优点不再赘述。
在这个拓扑电路中,线圈的品质因数影响很大,因此仿真时需要仔细计算电感电阻,在线圈计算工具中计算出电阻并考虑走线电阻,经过多次仿真和调整时序调整线圈。初步得到了比较好的仿真效果如下

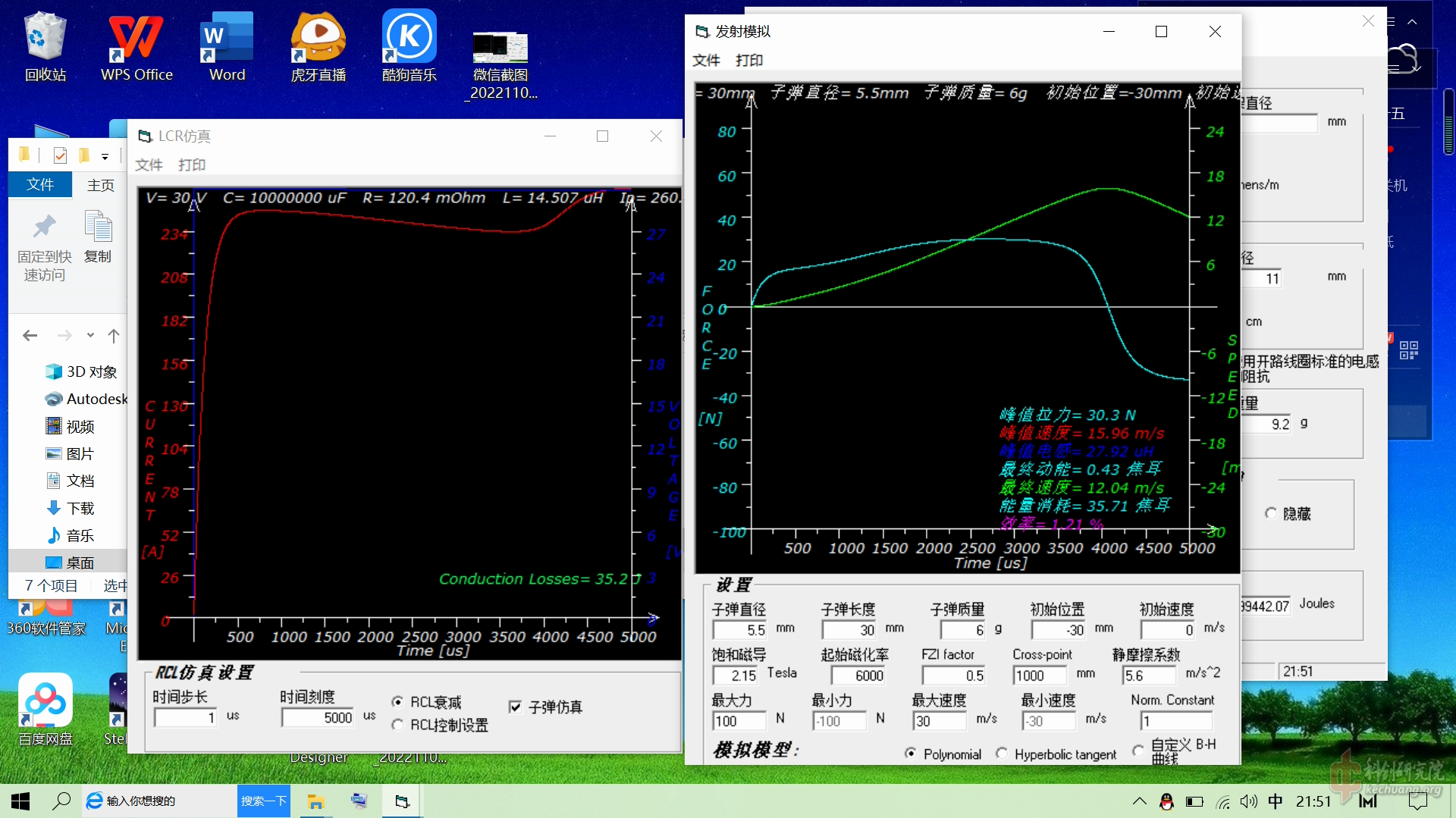
电流曲线如图

受力曲线
![)Z1DB)9`CH8OF6BK1V)2]DQ.png](https://img.kechuang.org:81/r/335725?c=resource)
速度曲线
![B@W]`PE)`M8APT06LS()_1E.png](https://img.kechuang.org:81/r/335726?c=resource)
可以看到后面在进入紧密加速阶段后,加速度始终维持在一个比较高的水平。
补偿电容电压
![L7ADXA7)ITJ`Z[38)%]MBH4.png](https://img.kechuang.org:81/r/335727?c=resource)
薄膜电容电压

薄膜电容电压在一个比较稳定的范围上,随着后级线圈电阻的下降,薄膜电容电压有小幅震荡上升的趋势,这可以对后期大电容电压下降后起到一定的补偿作用。
根据数据可以计算得效率大约为26.8%,这其中还包含了效率较低的前级,随着级数增加效率还能再提升一些。
目前看这个拓扑结合了buck拓扑和薄膜scr磁阻的优点,控制方式简单,电路精简,参数容易选择。相比boost拓扑,该拓扑可以在小电容情况下有着更低的内阻损耗。利用新拓扑的仿真出来的紧密连续加速的15级磁阻炮模型,取得了较好的效果,且具有很强的可行性。
[修改于 2年5个月前 - 2022/11/10 01:22:11]
对比boost效率高,主要得益于薄膜电容内阻低,但也有另一个因素,就是与脉宽和线圈有关。线圈电感量虽然更低了,但是也更短了,以致于时间常数τ=L/R不变或者高一些,脉宽也更小,即半波的角频率ω增高,线圈的品质因素Q=ωL/R=ωτ也增加(导致内阻损耗的比例更低)。
另外,是不是也因与波形有关,比boost更贴近正弦半波而引起的效率上涨,暂时没法下定论。
PS:经典薄膜磁阻暂时还没有传统薄膜磁阻的说法。在这之前圈内极为罕见的形式。
对比boost效率高,主要得益于薄膜电容内阻低,但也有另一个因素,就是与脉宽和线圈有关。线圈电感量虽...
线圈的时间常数,基本只取决于线圈的外形(还有材料电阻率和填充率),与线圈的电感量和匝数都几乎无关。线圈的尺寸越大,时间常数也就越大。所以你用更短的线圈必然会使时间常数降低,线圈的品质因数并不一定会增加。在RLC电路中电感工作频率等于谐振频率,此时电感Q值基本上只与材料和工艺有关了。
线圈的时间常数,基本只取决于线圈的外形(还有材料电阻率和填充率),与线圈的电感量和匝数都几乎无关。线...
没有吧,时间常数是与长短有关的,这点你说得对,但简而言之我认为是外径与长度之比越大,时间常数越高。
你看,如果同样是200uh,不改线径只压短线圈长度,是不是短线圈的时间常数更大呢?
还有,同样外径的线圈,压短线圈长度,是不是电感量变小了,而时间常数还是增大呢?
另外,因为谐振磁阻的线圈的电流上限更高,所以可以用更粗的线做低电感量而粗长比比较大的线圈,粗长比大的线圈的时间常数更高。
反正吧,谐振磁阻的脉宽能比boost拓扑磁阻的小很多,就拿我同弹丸尺寸,单级供能差不多的经典谐振与boost对比,谐振的脉宽基本上是boost的1/2大小。
至于线圈的Q值,我觉得谐振与boost一样,都是越往后因为初速就而效率越高,但谐振磁阻的效率随级数上涨得快许多。那为什么效率会逐级上涨呢,难道不是与Q值的上涨有关联吗?
好像磁阻是挺适合薄膜的,因为效率可以做的比较高但是其他的炮储能要求稍微一大薄膜的便携性就成大问题
没有吧,时间常数是与长短有关的,这点你说得对,但简而言之我认为是外径与长度之比越大,时间常数越高。你...
外径与长度之比越大,时间常数越高。
这个说法从经验角度来判断就不会是正确的,难道时间常数最大的是蚊香形的扁线圈嘛

取几个特值仿一下就能证伪,软件使用的是常用磁阻模拟器和https://www.kechuang.org/t/84939中的线圈参数计算器:
![]@`PQOG1AAJ3AXY`Q641(EL.png](https://img.kechuang.org:81/r/335730?c=resource)
![1]2W[5C6V6KIFKTB}W_IH]L.png](https://img.kechuang.org:81/r/335731?c=resource)
线圈1线圈2使用同样的线,使得电感量接近,只压缩线圈长度,可以看到线圈1相比2电感更大而电阻更小,因此有着更大的时间常数。
同样外径的线圈,压短线圈长度,是不是电感量变小了,而时间常数还是增大
这个从我前面回复中就说的是这种情况,线圈的尺寸越大,时间常数也就越大,(同外径)更短的线圈必然会使时间常数降低:
![]@`PQOG1AAJ3AXY`Q641(EL.png](https://img.kechuang.org:81/r/335730?c=resource)

boost是主动关断,谐振是过零关断的,当初始位置相同初速相同,谐振的脉宽自然是设置的要小一些的
效率随速度提升而升高具体原因我并不清楚。
好的,看来我说的有一半是错的。单依据外形的粗长比是无法判断时间常数的。应该是这样才能比:
得限制长度,比外径,外径大的时间常数高;
得限制外径,比长度,长度长的时间常数高;
得限制线径和电感量,才能用粗长比来比较时间常数,粗长比大的时间常数高。
好的,看来我说的有一半是错的。单依据外形的粗长比是无法判断时间常数的。应该是这样才能比:得限制长度,...
1,2点说的是对的,合起来就是我说的我说尺寸越大的意思。
第3点就是错的,我在上面的回复中已经证伪了。
外径与长度之比越大,时间常数越高。这个说法从经验角度来判断就不会是正确的,难道时间常数最大的是蚊香形...

不过,你这句话倒是点醒我了,可能也是为什么三水会提到正弦半波效率更高的原因了。
就是,如果给线圈恒定的电流,产生稳定的磁场,铁柱在较远的初始位置向线圈移动,铁柱所受到的电磁力是先增后减的,到铁柱中心与线圈中心重合时归零。
即就是说,在两中心相距比较近时,需要加很大的电流才能产生10N的力,而在上述的受力峰值处,加较小的电流就能产生10N的力。
不过,你这句话倒是点醒我了,可能也是为什么三水会提到正弦半波效率更高的原因了。就是,如果给线圈恒定的...
以半波为关键词进行搜索,没有在论坛找到你所说的半波效率更高的理论,只找到这样的话:
追求关断速度本身意义就不大,因为关断不是越快越好。让线圈电流瞬间归零,效率是比相对缓慢下降更低的,可以参考这篇帖子:https://www.kechuang.org/t/82437
效率最高的情况是:通过操纵各级线圈的电流,拟合出一个“截面是馒头形的线圈”,并让它始终在弹丸前方和弹丸保持相对静止。关断速度极快时,等效的是“方形的线圈”,效率并不是最高的。
以半波为关键词进行搜索,没有在论坛找到你所说的半波效率更高的理论,只找到这样的话:追求关断速度本身意...
其实是在Q群里说的,如果我没记错的话是提过一次馒头形波形是效率比较高的,几个月前了,我找不着记录了。按我的理解,正弦半波应该也属于他所说的馒头波形。
还有,
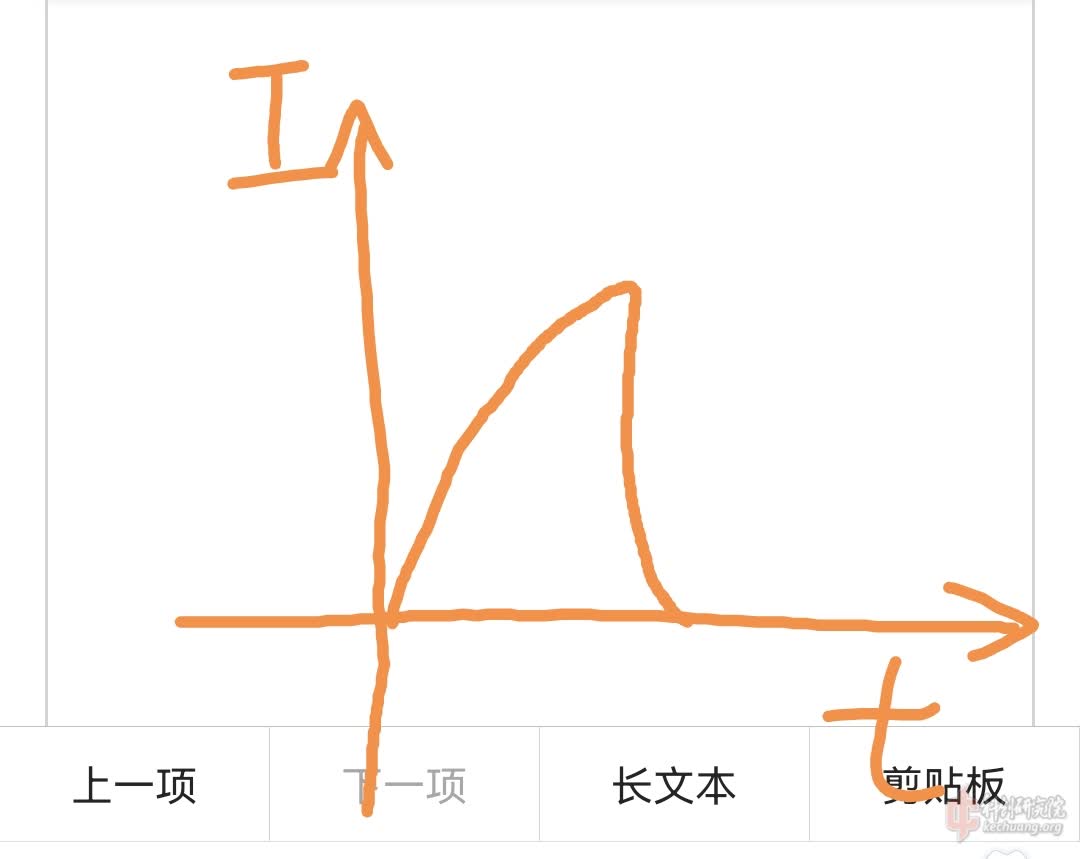
这种截波效率是比较低的,模拟器上试过,再怎么修改初始位置效率都是比较低的,原因是为啥,从上述应该可以得到一个合理的假设。
对比boost效率高,主要得益于薄膜电容内阻低,但也有另一个因素,就是与脉宽和线圈有关。线圈电感量虽...
其实我用脉宽来算品质因数,只是一种粗劣的算法,只为了估算和大概比较一下两个系统的电气参数的好坏。
在我手头上两台不同拓扑的炮都打8*20mm的蛋,差不多速度增量所对应级数的线圈所估算出来的品质因数,发现经典谐振磁阻的线圈品质因数确实是偏高。大概上涨40%。
牛逼啊,坐等新视频。
这一版本看起来是放弃纯时序又把光电用回来了是吗?如果是那样盲猜除中心拓扑做了改动应该和之前的Tk11总电路差不多。
不过还是想象不出具体电路上是怎么靠一个大电解电容和薄膜电容作为主要储能原件就能多级连续工作起来的

其实我用脉宽来算品质因数,只是一种粗劣的算法,只为了估算和大概比较一下两个系统的电气参数的好坏。在我...
这里回路中线圈的品质因数和选择的电容有关的,所以这品质因数完全取决于你的设计嘛。其实薄膜磁阻的性能和在零压关断的半桥是等效的。也就是说给半桥电路使用相同的电容和线圈并在零电压处回收得到的会是一样的效果。同样线圈和电容如果boost是对一个空电容回收,得到的效果也是一样的,只是对满电的电容回收电流下降更快。所以你认为薄膜磁阻效率更优的这一点是薄膜电容带来的。对于实际工程上,我更倾向于直接看效率来比较好坏。
牛逼啊,坐等新视频。这一版本看起来是放弃纯时序又把光电用回来了是吗?如果是那样盲猜除中心拓扑做了改动...
这一版本考虑使用纯时序加光电修正。
工作原理看主拓扑电路图和工作过程
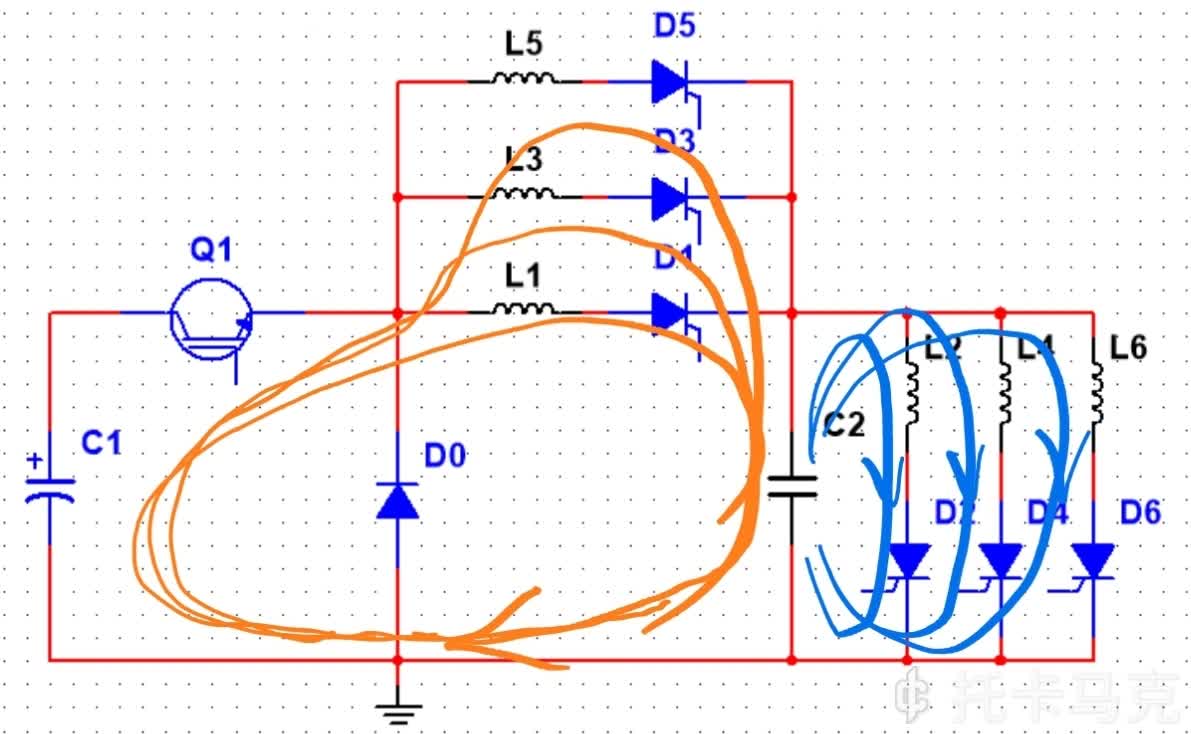
简单来说就是在奇数级开启时,用电解电容对薄膜进行补偿,来维持薄膜电容能量。
感觉有点不对啊,L2导通后感觉会对电容C2反向充电呀,好像会浪费能量。
200字以内,仅用于支线交流,主线讨论请采用回复功能。