所以说你到底要请教什么？

如何解释这个现象

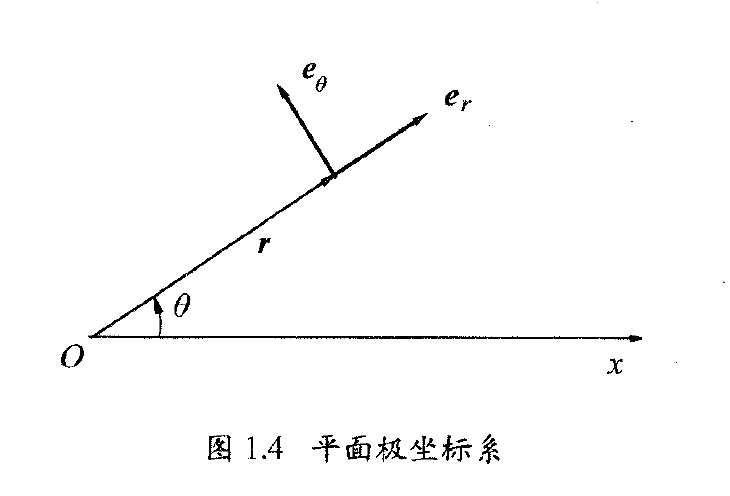
$$\mathbf{v} = v_r \mathbf{e}_r + v_\theta \mathbf{e}_\theta $$

可以看到，该坐标系的两个基矢是正交的。

对圆周运动（比如用绳子栓着的物体），我们将极坐标系原点放在圆心上。由于径向 $\mathbf{e}_r$ 上绳不可伸长，所以速度的径向分量为零，速度方向为切向。因为速度方向永远在圆周的切线方向上，当任一时刻失去绳的牵引（比如剪断绳），由牛顿第一定律可知，该物体会沿切线方向飞出。

（其实根据自然坐标系，运动轨迹都知道了，速度方向肯定就是切向）

楼主所说的物体有远离圆心的方向运动的趋势应该是指离心力吧?

应该明确一点:离心力是一种虚拟力，当一做圆周运动的物体失去提供向心力的力时，将向物体在在失去向心力时的方向继续运动，而此方向就是物体在圆上的切线方向。

这是用一个模拟器（游戏）模拟的视频

模拟.mp4 点击下载  

那物体在做圆周运动时为什么会有离心趋势？

有质量的物体具有惯性。使其在做圆周运动时有沿切线方向直线运动的趋势(远离圆心)。

我大概明白楼主要问些什么了。

牛顿运动定律中“物体总是保持当前的运动状态”中的“运动状态”的特征指标就是速度，此时我们必须注意到：这里的速度不仅有大小，而且有有方向，可以用高中数学中关于“矢量”的章节帮助理解。

在这个例子中，物体沿切线飞出，强调的是物体保持当前运动的方向：切线方向。

其实在这里我们也可以理解：为什么我们上初中的时候，每次描述运动时，不能说某物体做匀速运动，而是必须强调匀速直线运动。

这方面的书有《新概念物理（力学）》讲的相当详细，当然，学科交叉的程度也很深。

我们的物理老师一老diss我们学着物理忘了数学。。

这个概念没理解透彻的话，楼主理综很难上两百吧。

我想问的是 为什么物体在做圆周运动的时候 会有离心趋势 如果用惯性来解释的话 它应保持切线方向的运动趋势 但是物体保持的是远离圆心方向的力

我需要好好学语文了

需要搞清楚这个关系，是因为物体在没有任何外力作用下保持匀速直线的“切线”方向运动所以才需要向心力使其维持圆周运动，而不是因为圆周运动的物体有“离心的趋势”才会在放开物体时沿着切线方向运动。

物体运动分为受力或不受力。在不受力情况下，物体做匀速直线运动或静止状态；物体受力时，将不再做匀速直线运动，而改做变速运动，这个变速指的是直线变速运动、等线速度的曲线运动、变线速度的曲线运动。只要做匀速直线运动的不受力物体，其匀速或直线只要有一个量发生了改变，就可以断定物体受到了力的作用，就是受力运动，因为力是问题运动状态改变的量度，物体运动状态不变就可断定是不受力运动，物体运动状态一旦发生改变，其必受力。匀速圆周运动可以这样来理解，物体若不受力，将做匀速直线运动，但匀速圆周运动物体没有做匀速直线运动，而是做始终在改变方向的圆周运动，那么该物体必受到一个持续改变其直线运动方向的向心力的作用，使其保持圆周轨道作用。

        向心力和离心力是一对作用与反作用力。只有转动物体受向心力作用，不转动的物体没有向心力；向心力作用的效果是使本应作直线（沿切线方向）运动的物体，因受到垂直其运动方向力的作用，才改作圆周运动；转动物体对整个物体系统施以远离圆心的离心力作用，离心力作用于整个物体系统，它既作用于转动物体，也作用于承装转动的整个物体系统。向心力和离心力所在的同一直线不变，但随着转动物体位置的变动而改变，且符合牛顿第三定律。 

也就是说，你觉得在这个时候，物体应该沿物体与圆周运动的圆心的连线向外飞出？

用初中知识来讲的话呢，物体在合外力为零或者不受力的情况下将处于静止或匀速直线运动。而速度本身是一个矢量，具有大小和方向两个属性，对于在平面上做匀速圆周运动的物体而言，其速度的大小不变，方向却无时不刻不在变化。于是，必然有一个指向圆心的力存在使得物体运动方向不断改变。当某一时刻这个力消失，物体此时处于合外力为零的情况下，其运动方式将不再改变。即该物体将以向心力消失时刻的速度（包含该时刻的速度大小和方向）匀速运动下去。

向心力消失前，物体处于匀速圆周运动中，速度方向是运动轨迹在该点处的切线方向。于是向心力消失时，物体将以该时刻物体的速度（大小不变，方向就是消失前物体运动轨迹在该时刻处的切线方向）匀速直线运动下去

物体只受向心力时，向心力指向圆心，力可以看做圆的半径，物体位于圆上，以物体为一点作圆的切线，那么圆的半径当然是垂直于切线的，也就是说向心力于物体运动方向始终垂直，当物体失去向心力时也就会延切线方向飞出了

14楼阡陌徘徊讲的很好，支持，点个赞！

本来就没有所谓的离心力，也没有什么离心趋势。

有的只有使物体保持圆周运动的向心力，以及与向心力垂直的运动方向。

在物体没有飞出的时候，速度很快是，它有一种远离圆心的趋势，eg用手带动绳子转动一个物体，你会感到绳子会给你一个拉力，当然你松手时，物体会延切线方向运动。。。。

我最想问的是我的手为什么会感到一个力。。？

我当然知道松手后，物体会沿切线方向运动，而且还知道没有离心力，但我手上确实有个力。。。。

向心力的反作用力

严格的来讲，最好强调一下是在相对惯性系做曲线运动的非惯性系中的惯性力

在惯性系中，向心力与离心力是遵循牛顿第三定律的。这个问题是会被证实的。

没有理解，请再仔细讲一下。

其实可以这样看，所谓的向心力事实是空间的能量传递属性，当楼主用绳子栓住一个球开始旋转的时候，球获得了在空间中移动的能量，此时球得到了一个空间波动能量，该波动能量可以看做和球的旋转速度有关，也就是球的转速等于球空间震动频率。物质在空间匀速中运动并非如看上去那样是均衡的，它事实是组成球的原子核心中的希格斯玻色子以某种频率震动，当震动形成固定频率后这团球形物质获得了在空间中移动的能力。同时这个频率的空间震动通过绳子传递到楼主手中就被楼主的大脑误会成向心力。也就是空间缔能作用。物质要在空间中运动，你必须给予它足够的能量。所以楼主在给予球能量的时候，实际上是让这团球物质达到了某一频率的震动能级，你可以把在空间中运动的物体当做一种特殊的物质波。所以向心力不过是一种能量传递的波的假象。你手收到的拉力实际上是你的手到达了运动频率，手上的原子团获得了空间移动能量。

民科们要宣传自己的理论请回江湖版，不要在提问帖里胡说八道。

在定义中，没有向心力，所以根本没有离心力

没有向心力就没有圆周运动