一、大圆航线定义
球面上两点之间的最短距离的航线就是大圆航线。在航空业中,远距离航行的飞机规划航路时经常采用的航线。
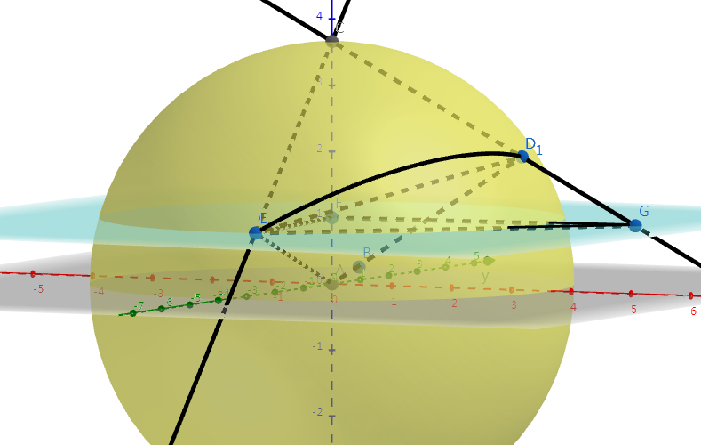
如图,弧ED1为E到D的大圆航线。
二、研究背景
问题起源
在生活中,我们经常乘坐飞机或轮船(有时候火车航线也能达到本文探索的尺度)之类的交通工具,当它们的航线跨度达到一定程度时,就不能近似地从平面上去计算航线的长度了,需要从球体的角度来算,这就是大圆航线的起源。那么,怎么去计算它的长度呢?

已知球面上两点的经纬度(球面上的坐标),求它们在球面上的最短连线的长度。

由于大圆航线可以看作一段劣弧,而地球的半径是已知的,所以最终要的就是求出这段弧所对的圆心角大小。那么我们可以先把这段弧所对的弦长求出,最后再根据弦长求得圆心角的大小。
三、研究过程

(1)从简单情况入手寻找解决思路
我们先探究了纬度或经度相同的情况
纬度相同时,借助三角函数,可以求出AK的值,AKB在同一平面上且该平面与赤道面相平,∠AKB为两地经度差,借助余弦定理变式即可求出AB长,在已知半径(AK)的圆K中,即可求出弧AB
经度相同时,连接AO BO(O为地心),已知∠AOB(即纬度差),可以直接利用圆心角及半径求出弧AB,但也可以再次利用余弦定理求出AB,再求弧AB
由特殊情况中,我们找到了初步思路:求两点间连线线段的长度,即AB
2)将思路拓展至一般情况
①A点与B点同在北半球的情况
这时∠OAK=A点的纬度=a,可求出sin a的值,根据r的长度可算出OK的长度k,所以


得出AN,BN长度后,延长NB至交A所在纬度圈的平面(令为⊙K)于点B`,连接KB`,此时因为A,K,B`在同一平面上,故B`K⊥NO,即B`K//BF。此时,∠AKB`的度数即为x与y的差值。OB和ON相等,又由B点的纬度得到∠BON的度数,故可以求∠ONB的度数。
因为∠NKB’=90︒,∠ONB’=∠ONB,可求得KB’=tan∠ONB’·KN,又结合之前求得的AK与∠AKB`的度数可求AB`的长度。这样,我们就有了AB`,AN以及NB`的长度,根据余弦定理可求出∠ANB度数。最后,再结合AN和NB的长度,求得AB的长度b,由弧长公式L=2r·arcsin (b/2r)就可求出弧AB的长度了,如图2。

②将思路拓展至一般情况
② A与B在不同的南北半球
这里步骤基本与上条一样,仅∠KAN(∠FBN)需要加上A(B)点的纬度绝对值之一半以配合南北纬的差异。
③A与B点同在南半球
同①,只需将参照点N替换为南极点S即可。
(3)整理模型并求出公式
A,B同在北半球
已知A(a,x),B(b,y)∵∠OAK=a, ∠OBF=b∴OK=r·sina,OF=r·sin b∵ON=r
∴NK=r-r·sina,NF=r-r·sinb
∵∠AKO=90︒
∴由勾股定理求得AK,BF的值,再利用AN2=AK2+KN2 BN2=BF2+NF2求出BN,AN的值
延长NB交⊙K所在平面于点B`,连接KB`,AB`
∴KB`⊥NO∴KB`//FB
∴∠AKB`=x-y,
∠NKB`=90∵ON=NB∴∠ONB=∠OBN∵∠BON=90°-b ∴∠ONB=45°+b/2∴∠ONB`=45°+b/2
∴∠ANB`=∠ANB=cos-11/2AN·NB’·NB’2+AN2-AB’2
AB=√AN2+BN2−2AN·BN·∠ANB
最后代入弧长公式L=2r·cos-1(b/2r)即可求得大圆航线lAB的长度
所以,最终的公式为


由于公式较为复杂,不便于日常计算,我们便打算通过编程的方式,让电脑帮我们运算,我们最终的代码如下:



对于该公式与编程,我们可以将其利用到生活中,如对于航天公司和旅客,可以很方便地求出出发点至中点的最短距离的近似值,从而合理规划航线,减少时间浪费。
(7)拓展与改良

这里我们为了简化计算,球的半径设为1。
前面已经说过,A点的纬度为a,经度为x,B点的纬度为b, 经度为y。如图3所示,作AI⊥平面xOy于I,BH⊥平面xOy于H,AI即为A的z坐标,BH即为B的z坐标,
故AI= rsin a,BH= rsin b,可推出
OI=rcos a,OH=rcos b。再分别过H
和I向x轴、y轴作垂线,由OI和OH
的长度和x、y的大小可以算出A点
与B点的横纵坐标如下:
A(rcos a sin x,rcos a cos x,rsin a),
B(rcos b sin y,rcos b cos y,rsin b)



我们在借助了三角函数与余弦定理等数学工具的条件下,推导出了大圆航线长度的计算公式,并利用Python面积出了相应的程序,解决了本文开头留下的问题。