一、引言

二、背景问题

三、介绍模型

四、实际运用

一、引言

生活中处处有角度。例如大雁的“人”字形队伍有固定的角度，蜂房底盘上有固定的角度……而每当我们在绿茵场上观看球赛时，我总会想：运动员射门成功的可能性是否也与角度有关呢？带着这个问题，我们小组展开了研究。

在足球赛中，射门是一个关乎成败的关键要素。在射门时，哪个位置更容易得到更优更大的射门角度呢？我们不妨将球门（AB)、发球点(P)、发球线(l）简化为一个数学模型，如图1-1：

那么什么地方，射球角度最大呢？

转化为下面这个问题，如图1-2：  已知定点A，B，动点P在直线l上，请问P运动到什么位置时，∠APB的值最大呢？

在平面中去求一个角度的大小，或者去寻找一个固定角度的位置，我们的第一反应就是把它和圆联系在一起，将问题简化。

首先，我们要构造圆，如何构造？

我们以∠APB为圆周角，AB为对应的弦长，画圆，也就是画三角形APB的外接圆。如图1-3

当点P在直线l上运动时，∠a和∠b有着怎样的关系？怎样使得∠a最大？

根据我们初三上学期所学的圆周角定理，可得∠a等于∠b等于二分之一∠AOB。

要使∠a最大，也就是使∠AOB最大。

那么如何使∠AOB最大呢？

视频1.mp4  点击下载 ‎

通过观察我们发现，想要∠AOB大，圆心得往下，半径要尽可能小。但是圆不可能一直小下去，必须和直线l有交点才行。通过画图我们发现圆与直线相切的时候，∠AOB是最大的，即∠A是最大的，如图1-4。此时，我们的问题就解决了。

1-4

我们发现不管题目怎样变幻，思路都是万变不离其宗的，可以根据以上的验证思路总结出两定一动角度最值问题的基本做题步骤（简称两垂三步法），解题步骤如下：

1.找定点，作中垂线；

2.找圆心，向直线作垂线段；

3.垂线段等于半径列方程。

三、介绍模型————米勒原理

就这样，我们解决了最基本的两定一动角度最值问题。之前我们研究的两定一动角度最值问题，实际上就是米勒定理。

米勒定理是这样描述的：

已知，点A、B是∠MON的ON边上的两个定点，C是OM边上的一个动点，当c在何处时，∠ACB最大?问题的答案是:当且仅当△ABC的外接圆与边OM相切于点C时，∠ACB最大。

这个定理是德国数学家米勒提出的。米勒是欧洲最有影响力的数学家之一。他发表的《三角学说》是使得三角学在欧洲取得独立地位的第一部系统性著作。

米勒提出的疑问

在当时，米勒提出了一个有趣的问题：在地球表面什么部位，一根垂直的悬杆呈现最长？即在什么部位，视角最大？

米勒问题面对的是在地球上的实际测量问题。与地球相比，一根旗杆，小到可以忽略不计，因此人们把问题进行简化，将米勒问题放到二维平面上去研究，演变成现在的两定一动角度最值问题。如图2-1

四、实际应用

问题：在大礼堂上，长达4m的聚光灯悬在空中（线段BC为聚光灯）要时聚光灯光线会聚在对面的墙上，且要使投射角最大(AD为墙，∠BPC为投射角）如何取点使投射角最大呢？ (两线段之间的距离为7m）

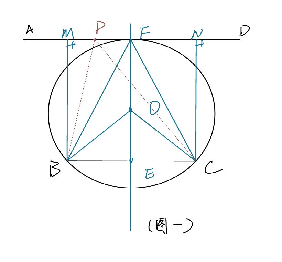
这个问题我们可理解为：现有两条平行线段，它们间的距离为7m，B C小于AD，BC等于4m，点P在AD上运动，点P在哪里时∠BPC最大？如图3-1

对此，我们要进行分类讨论1.当点P在线段MN间运动时

1.当点P在BC的中垂线上时

首先取BC的中点E，过点E作EF⊥AD，连接BF与FC，连接BO与OC，作△BCF的外接圆，外心记为O。圆与AD相切于点F，则∠BFC=½∠BOC。

2.当点P在MF或FN之间移动时

过点B、C分别作BM⊥AD，CN⊥AD。当点P在点M、点N之间运动（不与点F重合），连接BP与CP，CP与⊙O相交与点H，连接CH，可得∠BHC＞∠BPC。

∵∠BHC=∠BFC

∴∠BFC＞∠BPC

综上，当点P在点M、点N之间运动（不与点F重合）时，∠BFC始终＞∠BPC。

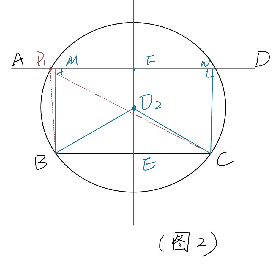
2.当点P在线段MN外运动时如图3-1、图3-2

当点P在点M、点N外运动时（如图3-2），连接BP_1与CP_1，作△BP_1C的外接圆，外心记为O_2，连接BO_2与CO_2，则

∠BP_1C=½∠BO_2C。

经多次验证，我们得出结论：当△BP_1C是钝角三角形时（即∠P_1BC或∠P_1CB为钝角时），EO＜EO_2。

∵∠BOC＞∠BO_2C

∴∠BPC大于∠BP_1C

根据以上两个分类讨论，我们最终得出结论：当点P运动到BC的中垂线时，∠BPC最大，即投射角度最大

（一）总结

    在研究、探索两定一动角度最值问题的过程中，我们先将问题简化，再将有关圆的知识和定理进行迁移运用，将该数学模型放在圆中继续探究。这也是初中数学“隐形圆”的用法之一。在坐标系计算中，我们还用到了八年级的垂直平分线知识，计算出点的坐标。最后，我们溯流求源，挖掘出这背后的米勒定理以及相关的演变过程。