基于百度的公式

基于numpy等库进行开发

也可以直接下载打包好的程序

但还是推荐复制代码自行编译，代码在最后

以下是介绍

冯·卡门曲线的功用不再赘述，因为百度比我更准确

以下是程序（不更新）

冯·卡门曲线计算器（仅供娱乐）.zip 39.33MB ZIP 60次下载

以下是算式

\[\begin{array}{l} \theta {\rm{ = }}{\cos ^{ - 1}}(1 - \frac{{2x}}{L})\\ y = \frac{R}{{\sqrt \pi  }}\sqrt {\theta  - \frac{{\sin (2\theta )}}{2} + C{{\sin }^3}\theta } \end{array}\]

解析

L是长度

R是半径

在之后可能会继续更新

以下是效果图

在显示图标之后命令行窗口弹出的数据即为取样点和计算结果

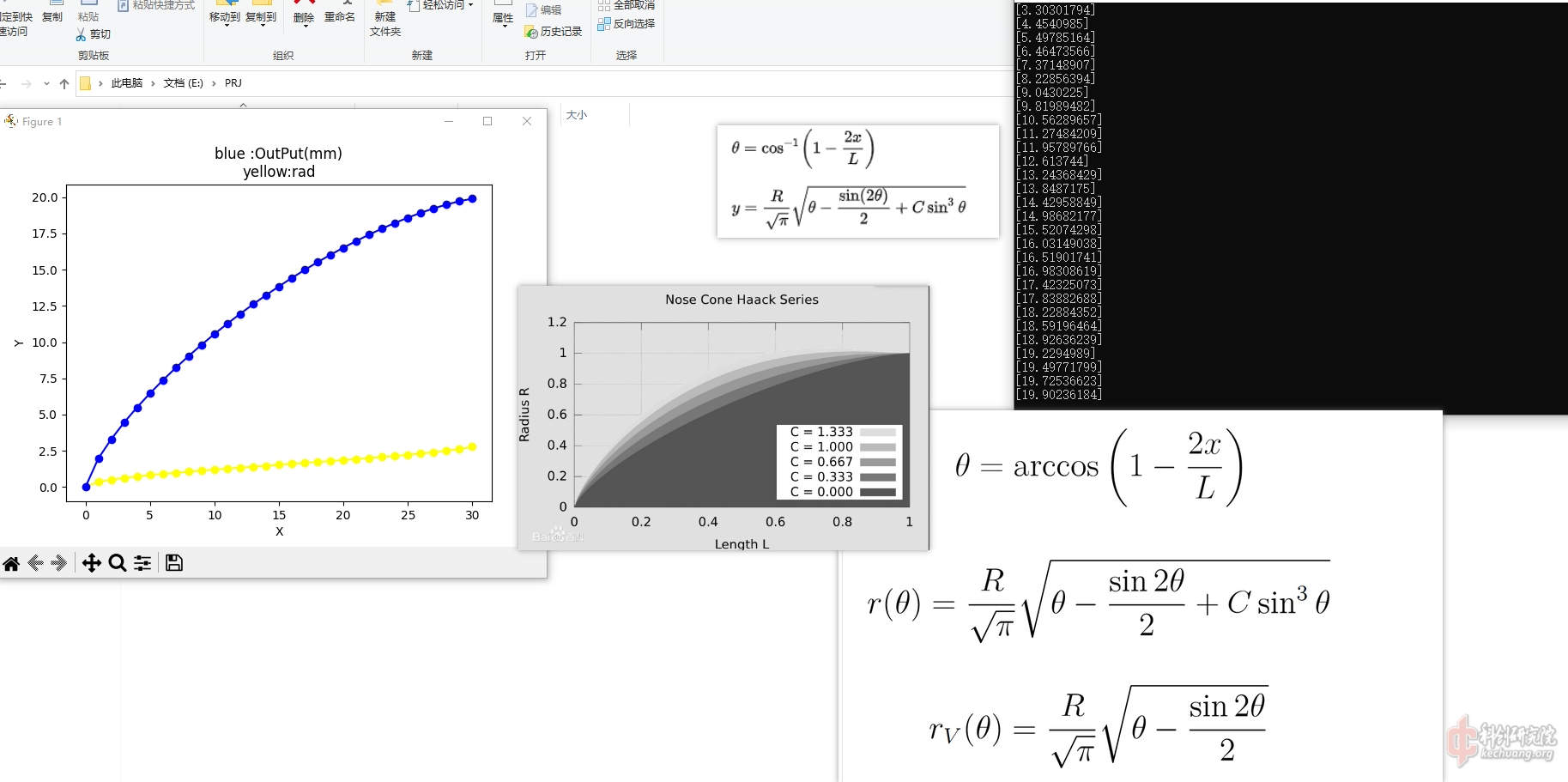
C = 1/3时的图像-20230909更新

新添功能：自动比较出于目标直径最靠近的点

以下是代码（暂时停止同步，最近一次同步发生在20230910）

import math
import numpy as np
import matplotlib.pyplot as plt

print("冯·卡门曲线计算器——仅供娱乐"
      "\n版本号0.0.0.dev\n"
      "LD-Haack C= 0\n"
      "暂未启用(LV-Haack C= 1/3）\n"
      "长度最长30单位，宽度无限制,命令行输出即为结果")
PLong = 30 + 1#长度为30
#PLong = int(input("长度：")) +1
Xlab = [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]#取样点，长度
#
ROP = 20#末端直径
#ROP = int(input("半径："))
Syssign = 1
Count = 0
XOIP = [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]#暂时存储数据的容器，取样点有多少它就得有多少
Yout = [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]#输出点，同上要求
pai = [3.14159265]

MODEset = 2# 如果模式设置为2 ，则C=1/3 1则为C=0

while(Syssign):
    SentPL = 0.00
    SentPL = 2*Xlab[Count]/PLong
    #print(SentPL)
    XOIP[Count] = 1-SentPL
    Count += 1
    if(Count == PLong):
        Syssign = 0
        Count = 0
ARCX = np.arccos(XOIP)

plt.plot(Xlab, ARCX,
         color='yellow', marker="o")
Syssign = 1
while(Syssign):
    XOIP[Count] = ARCX[Count] * 2
    Count += 1
    if(Count == PLong):
        Syssign = 0
        Count = 0
XOIP = np.sin(XOIP)

Syssign = 1
while(Syssign):
    XOIP[Count] = XOIP[Count] / 2
    Count += 1
    if(Count == PLong):
        Syssign = 0
        Count = 0


Syssign = 1
while(Syssign):
    XOIP[Count] = ARCX[Count]  - XOIP[Count]
    Count += 1
    if(Count == PLong):
        Syssign = 0
        Count = 0
#如果情况是C = 0则忽略该段，如果是1/3还需要加一个1/3Sin角度的三次方
Syssign = 1
CSINT = ARCX
Count = 3
while(Count >=1):
    CSINT = np.sin(CSINT)
    Count -= 1
print(Count)
Count = 0
if MODEset == 2:
    while(Syssign):
        CSINT[Count] = CSINT[Count]/3
        XOIP[Count] = XOIP[Count] + CSINT[Count]
        Count += 1
        if(Count == PLong):
            Syssign = 0
            Count = 0
#
XOIP = np.sqrt(XOIP)
pai = np.sqrt(pai)

Syssign = 1
while(Syssign):

    Yout[Count] = XOIP[Count] * ROP/pai#注意，这里是根号pai
    Count += 1
    if(Count == PLong):
        Syssign = 0
        Count = 0

Syssign = 1
while(Syssign):
    print("\n\nX:")
    print(Xlab[Count])
    print("Y:")
    print(Yout[Count])
    Count += 1
    if(Count == PLong):
        Syssign = 0
        Count = 0

plt.plot(Xlab, Yout,
         color='blue', marker="o")

#plt.plot(Xlab, out_array2,
#         color='red', marker="o")

plt.title("BLUE:OUTPUT\nyellow:rad")
plt.xlabel("X")
plt.ylabel("Y")
plt.show()

以下是实现临近匹配的，由于属于另一个项目，因而只把部分功能实现到这里

while(Syssign):
   print("\n\nX:")
   print(Xlab[Count])
   print("Y:")
   print(Yout[Count])
   if Yout[Count] <= FOPC:
       ZDsign = 1
   if ZDsign == 1:
       if Yout[Count] >= FOPC:
           ZDsign = 2
           print("数据的最近似点已采集")
           #由于是最靠近的较大数字，因此用减去较小数字来实现逐步逼近的效果

           EPSD = Count
           print(EPSD)
   Count += 1
   if(Count == PLong):
       Syssign = 0
       Count = 0

可以自行寻找合适的点进行替换（但其实不如自己插入进去）

20230910