昨天发了个帖子将如何选择电压偏置电路中的固定电阻问题：https://kechuang.org/t/86931

今天干脆拓展一下，讲讲如何用热敏电阻代入电压偏置电路来计算得到温度值

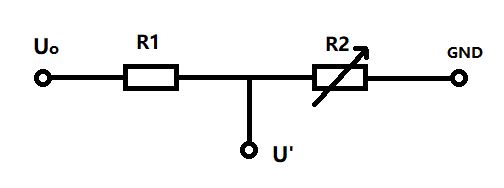
电路

电路还是那个电路，取而代之的是R2使用NTC热敏电阻

热敏电阻

       NTC热敏电阻，顾名思义就是其电阻会随着温度的升高而降低，还有另一种叫PTC热敏电阻，其电阻会随着温度的升高而升高，但有个很大的问题就是其变化是非线性的，如果我们希望测量47℃-87℃的温度值，寻找到一款热敏电阻的温度-电阻数据表：

因为电阻-温度的变化是非线性的，我们可以对离散型数据进行拟合，这里采用了对温度-电阻的数据进行了反比例函数的拟合：

此款热敏电阻的温度（x）- 电阻（y）的关系式为：1/y=1.5631-65.9820/x

其在工作温度范围内的电阻变化约为(1k,4k)，则我们可以带入我们所推导的公式(参考开头链接文章)得到我们所需的固定电阻R1=2k,此时我们可以得到偏置电压和可变电阻的关系如图下：

电阻（x）- 电压（y）的关系式为：y = x/(2+x)

拟合偏置电压关系式

在该电路下的偏置电压与可变电阻的关系为非线性变化，为了在adc采集完后能更好地进行数据处理，又因为在该函数下不容易拟合处理，所以我们可以用对数函数进行回归拟合。

在有效范围内我们在曲线上取十个任意点作为精准采样点，然后将十个点的坐标进行对数函数拟合，我们可见进行对数拟合后在有效范围内的拟合效果极佳：

绿线-原方程

黑线-对数拟合方程

原方程为：U' = x/(2+x)

拟合方程为：U' = 0.3278 + 0.2456ln(x)

电压温度关系式

对电压-电阻拟合方程取反函数得到：R = e^[(U'-0.3278)/0.2456]

将其代入电阻-温度拟合方程得到：e^[-(U'-0.3278)/0.2456]=1.5631-65.982/T

再取反函数得温度关系式：

T = 65.982/{1.5631-e^[-(U'-0.3278)/0.2456]}

    其中的U'是单片机adc取样得到的电压值，经上式可以直接处理为温度值，若R1使用按照推导公式得到的电阻，则能在该电路中得到理论最高精准度，在一定程度上可以取代在单层电路中麻烦的电桥式拓扑结构，大大地简化了电路设计。

公式由个人推导，若有错误欢迎大佬们前来指出！