以往在该电路设计中R1都是十分随意得取一个R2变化区间的中值,一直不知道该如何较好地选择一个较好的固定电阻值,本文讲述该如何选择其中的固定电阻值。
电压偏置测量电路
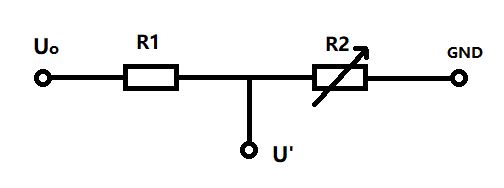
该种电路多应用于变电阻传感器的测量,如红外接收器,压变电阻等等,在可变电阻R2改变的时候,U’得到的电压也随之改变,其电压该为电路上R2占据的电压,则变化规律满足以下公式:
U’=R2/(R1+R2)
实际应用
在应用中,R2为传感器件,受到外部刺激时其电阻会随之改变,从而U’的偏置电压发生改变,该电压传入单片机进行adc采集后得到数字信号。在设计中我们希望有一个较好的测量效果,得到一个较大的测量范围,我们只能改变R1的电阻值。
在实际传感器中,如红外接收器,其电阻值会随着接收到的有效光强的增强而下降,在工作光强内对应着一个红外接收器的电阻区间,我们希望在该电阻变化区间内所对应的U'有个较大的变化范围,这样在有限位数的adc中得到更好的精度。
如何选值
在选值中,固定电阻的过大或过小都会导致偏置电压变化范围变小,为了在电阻变化区间中为了得到一个较大的U'变化区间,我们需要对R1的选值进行分析。
我们假设R2的电阻变化范围为(X1,X2)得到的偏置电压为U',我们已知其关系为:
U'= X/(R1+X)
所以偏置电压的变化为:
ΔU = X2/(R1+X2) - X1/(R1+X1)
令
g(R1)= ΔU = R1(X2-X1)/(R1+X2)(R1+X1)
为使g(R1)有最大值,我们可对g(R1)求导,并令其等于0,在该时的R1值对应的ΔU有最大值,所以有:
g'(R1) = (X2-X1)[R12+(X1+X2)R1+X1X2-2R12-(X1+X2)R1]/[R12+(X1+X2)R1+X1X2]
令其等于零即:
(X2-X1)[R12+(X1+X2)R1+X1X2-2R12-(X1+X2)R1] = 0
最终得:
R1 = [(X1X22-X12X2)/(X2-X1)]1/2
在该固定电阻下,R2在电阻变化范围(X1,X2)中时可得到较大的ΔU,这样可以得到更大的adc采集范围,从而提高测量精度。
拓展
在该电路下的偏置电压为非线性变化,为了在adc采集完后能更好地进行数据处理,因为在该函数下不容易拟合处理,我们可以用对数函数进行回归拟合,在有效区间内的拟合效果十分理想。
若需要更高精度的测量电路,则可以考虑电桥式测量电路,但在该电路中电阻需有较高精度,且较偏置电路复杂。
推导由个人完成,欢迎指出错误
[修改于 3年8个月前 - 2021/08/09 15:47:16]