Kalman Filter

之前考虑做飞控玩，所以研究过一下 kalman filter相关的数学模型和实际使用，在此做个整理以及记录编程实验。

本来想归到之前的机器学习笔记中去，毕竟 kalman filter 是属于 Bayes' Filter 实际使用中的一个特例，跟机器学习中的Hidden Markov model (HMM) 有着牵不清扯不断的联系，其求解思路归结起来就是EM （Expectation Maximization），以至于EM维基词条中提供的例子就是kalman filter。但考虑到一般的传统，还是单独归入控制技术更为科学。

首先解释什么是 bayers' filter。

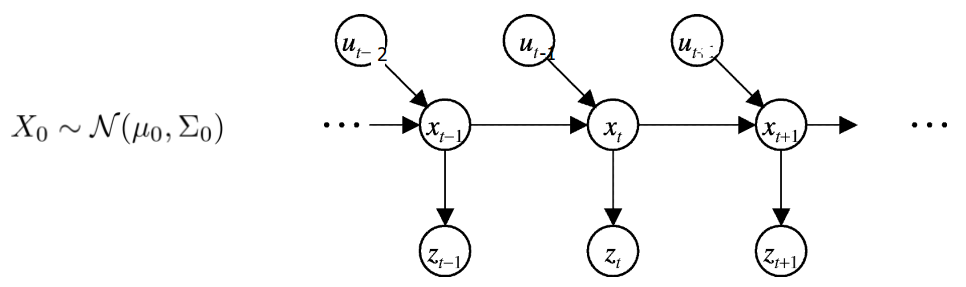
在这个图中，我们有一系列 hidden state variable \(x_t\)，hidden 意味着不可直接观测，只能通过间接的 measurement variable \(z_t\) 来获知。举个例子就是，过去的航海者在海上航行时是无法直接知道自己船的位置和速度的（对比于GPS），所以只能间接通过测量岸上的地标用三角测距来获取。这里船的位置、速度就是 \(x_t\)，而三角测距读取的角度，就是\(z_t\)。而对于船当前状态的了解，又往往和过往时刻的历史状态有密切关系，比如过去的水手会在海图上不断更新当前位置坐标，以此获取航向、速度信息。最后 \(u_t\) 则是可以影响当前状态的输入控制，比如船长每个时刻的打舵量。

如图所示，在HMM中，每一时刻的状态只和紧邻着的上一时刻的状态有关，每一时刻的测量只和当前时刻的状态有关（虽然啰嗦但还是注明以免混乱）。同时在 kalman filter 中，hidden state variable \(x_t\) 和 measurement variable \(z_t\) 都是假设为服从高斯分布的，这种近似能够对付大部分的实际情况。

写成公式形式就是：

$$ P(x_t|x_{0:t-1}, z_{0:t-1}, u_{0:t-1})=P(x_t|x_{t-1},u_{t-1}) $$ $$ P(z_t|x_{0:t-1}, z_{0:t-1}, u_{0:t-1})=P(z_t|x_t) $$

对 \(P(x_t|x_{t-1},u_{t-1})\) 的描述，在 kalman filter 中被称作 process model，表示当前状态\(x_t\) 受前一时刻状态 \(x_{t-1}\) 和输入 \(u_{t-1}\) 的影响： $$ x_t=Ax_{t-1}+B u_{t-1}+n_t $$

其中 \(n_t\) 是加性白噪声，注意这里的状态转换矩阵 \(A\) 形容的是一种线性关系，作为computer visoner，我更喜欢叫做仿射变换，放到运动中，就是最简单的平移关系。但大部分实际情形都是非线性的，简单举例就是普通 kalman filter 可以对平动滤波，但转动就没办法了。解决办法是用 extended kalman filter 或者 unscented kalman filter，他们各自用不同的方式对非线性做了线性近似，然后就可以用普通的 kalman filter 处理。

而对测量过程的描述，称作 measurement model，同样，还是一种线性关系：

$$ z_t = C x_t + v_t $$

这样一来，如前所述，在 \(t\) 时刻我们将会得到两个对于当前状态的估计，一个是来源于 process model 预测的先验状态 \( {\hat{x_t}}^-\)，由上一时刻状态 \(x_{t-1}\) 推导而来，- 表示在 \(t\) 来临以前就可以获取这个状态， 比如四轴飞行器中，通过刚体运动的动力学方程，可以预测下一时刻的飞行姿态；另一个是使用 measurement model 通过测量的 \(z_{t}\) 反推的后验状态 \( {\hat{x_t}}^z\)，比如四轴飞行器当前时刻从 IMU 读取的值解算出的姿态。这两个状态变量均服从高斯分布，而高斯分布的一个特性就是，两个高斯变量的加权和，仍然服从高斯分布。而通过选取恰当的加权权重，可以使这个新的高斯分布的分散程度（ error covariance）小于之前的任一个， 如下图所示。

这使得将 \( {\hat{x_t}}^-\) 和 \( {\hat{x_t}}^z\) 重新组合得到一个更精确状态量预测成为可能。

实际使用的组合方式是这样的：

$$ \hat{x}_t={\hat{x}_t}^-+K(z_k-C{\hat{x}_t}^-) $$

其中 \(K\) 被称作 kalman gain 或者 blending factor，我们将恰当的选择 \(K\) 以使得 \( \hat{x}_t \)的 error covariance 最小。\((z_k-C{\hat{x}_t}^-)\) 被称为测量残差（residual），表示实际测量值 \(z_k\) 与预测测量值 \(C{\hat{x}_t}^-\) 之间的偏移。

下面给出推导过程（感觉像有100年没有推过公式了）：

首先我们的 \(\hat{x}_t^-\) 和 \(\hat{x}_t\) 分别服从如下高斯分布的：

$$ \hat{x}_t^- \sim \mathcal{N}(\mu_t^- , \Sigma_t^-), \quad \hat{x}_t \sim \mathcal{N}(\mu_t , \Sigma_t) $$

$$ \Sigma_t^-=E[(x_t-\hat{x}_t^-)(x_t-\hat{x}_t^-)^T] $$

$$ \Sigma_t=E[(x_t-\hat{x}_t)(x_t-\hat{x}_t)^T] $$

其中 \(x_t\) 是实际的状态值（对应于预测值）。

然后 measurement model 有：

$$ z_t=Cx_t+v $$

$$ v\sim \mathcal{N}(0 , R) $$

$$ R=E[vv^T] $$

我们对 \(K\) 优化的目的是使最终的 \(\Sigma_t\) 的 \(trace (Tr)\) 最小，为什么是 \(trace\) 呢？ 因为我们知道 \(\Sigma_t\) 是一个对角矩阵，且所有项都大于零，所以它的 \(trace\) 等价于它的 \(L1 \;norm\)，所以相当于用 \(L1\; norm\) 作为 loss function 进行了一次数值优化。这里我们令：

$$ K=arg \max_{K} \, Tr(E[(x_t-\hat{x}_t)(x_t-\hat{x}_t)^T]) $$ 对右边括号内展开：

$$ E[(x_t-\hat{x}_t)(x_t-\hat{x}_t)^T] =E\{ [x_t-\hat{x}_t^--K(z_t-C\hat{x}_t^-)][x_t-\hat{x}_t^--K(z_t-C\hat{x}_t^-)]^T \} $$

$$ =E\{ [x_t-\hat{x}_t^--K[C(x_t-\hat{x}_t^-)+v]][x_t-\hat{x}_t^--K[C(x_t-\hat{x}_t^-)+v]]^T\} $$

$$ =-\Sigma_t^-C^TK^T-KC{\Sigma_t^-}^T+K(C\Sigma_t^-C^T)K^T+KRK^T $$

然后令： $$ f(K)=Tr[-\Sigma_t^-C^TK^T-KC{\Sigma_t^-}^T+K(C\Sigma_t^-C^T)K^T+KRK^T] $$

$$ \frac{\partial f(K)}{K}=0 $$

这里要用到几个重要的 \(trace\) 求导公式：

$$ \frac{\partial \;Tr(XA) }{\partial X}=A^T $$

$$ \frac{\partial \;Tr(X^TA) }{\partial X}=\frac{\partial \;Tr(AX^T) }{\partial X}=A $$

$$ \frac{\partial \;Tr(XBX^T) }{\partial X}=XB^T+XB $$

所以最后得到一个结论：

$$ K=\frac{ \Sigma_t^- C^T }{C\Sigma_t^-C^T+R} $$

跟其它资料上给出的形式是一样的（做这一堆展开简直要了命。。）

对这个结果的一个非常有趣的解释是，当测量结果的 error covariance \(R\) 趋近于 0 时，测量值 \(z_t\) 是完全没有误差的，这时有： $$ \lim_{R \to\ 0} K=C^{-1} $$

代入 prediction 公式中得到：

$$ \hat{x}_t=C^{-1}z_t $$

也就是说只剩下了通过测量得到的部分。

而当预测值的 error covariance \(\Sigma_t^-\) 趋近于 0 时，预测结果 \(\hat{x}_t^-\) 是完全准确的，此时有：

$$ \lim_{\Sigma_t^- \to\ 0} K=0 $$

于是会得到：

$$ \hat{x}_t=\hat{x}_t^- $$

只剩下了通过预测得到的部分。

这里的绝妙之处就在于，\(K\) 会根据测量值 \(z_t\)、预测值 \(\hat{x}_t^-\) 各自的置信程度，来自动调整二者的权重，使得权重偏向于更可信的那一方。

到目前为止，我已经推导出了 kalman filter 的两大重要步骤，Prediction 和 Update，分别对应 EM 算法中的 Expectation 和 Maximization，其图示如下：

反复不断重复这两个过程，即是 kalman filter 的实现形式。

Extended Kalman Filter

虽然以上已经成功推导了 kalman filter 的全部公式，但是楼主想做的是四轴姿态估计，原始的 kalman filter 只适用于如下这种线性情况，也就是说，前一时刻状态的高斯分布，经过状态变换后，仍然是高斯分布。

但在强大的微积分面前，一切都是浮云。

人们为了解决非线性，提出了 Extended Kalman Filter （拓展卡尔曼滤波）。其思路是在传递曲线局部用该点的切线方程来代替曲线本身，其实就是高数中的一阶泰勒展开。这样形成了一种局部的线性关系，可以使用原本的 kalman filter 的公式进行运算，只是传递矩阵 \(A\) 不再是恒定的，而是随时刻变化的 \(A_t\)，需要在每一时刻根据导数重新计算 。