有趣的探索——由一道物理高考题到独立推导齐奥尔科夫斯基公式

文号t78746

64983

FROZEN巨擘2016/02/01喷气推进 IP:广东

最近都要忙于高考备考，所以一切的火箭试验活动都被勒令暂停了（其实不被勒令我也不敢玩了，毕竟是高考。。。）。不过其实我还是有计划在空闲的时候看一点理论的，不过我现在脑子好像废了，碰到点用脑子的课外书就会严重的头晕，看来是泡课本太多了（这么说来课本里的东西不用脑子的！？嗯。。。），所以还是放弃了这个计划。不过有意思的是，一个月前随着物理复习到冲量，有关火箭的计算也开始多起来，最后竟然跳出来了一道令我百思不得其解的高考题（不过超级纠结了一周多以后还是想明白了，不然也就不会发这个帖子了(^~^)）。所以就趁宝贵的几天寒假来给大家分享一下我的整个思考过程，说不定能加深对冲量的理解和火箭工作基本原理的认识。自然高中生学识有限，有错误还望指教。

那一周多来用的草稿纸，比较乱。。。还有更多的YY无法拍照。。。

这就是那道神奇的物理高考题，再下面是就是它的答案。题里的图太丑了。。。

题目很简单：证明火箭不是一次把燃气喷完而是逐渐向后喷气以获得更大反冲速度的道理

第一眼看到这道题下意识的就想利用齐奥尔科夫斯基公式解决，但是看完题目就惊讶地发现要我证明的是一个和齐奥尔科夫斯基公式完全违背的物理命题！！

首先从答案，我们可以很清楚地知道他把火箭燃料当做三个质量都为 m 的刚性小球（以为证明：在抛出的速度都与火箭的相对速度都为 V 时，法一：一次性抛出三个小球（燃料）和法二：分三次分别抛出一个小球（燃料）后火箭的速度有何不同）。答案公式多不好编辑，以下是答案简要：

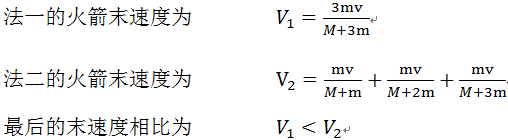
所以第二种方法可以使火箭获得更大的末速度！！但我知道，知道齐奥尔科夫斯基公式的人都会认为这是不可能的，因为从齐奥尔科夫斯基公式的表达式可以知道：火箭的最终速度只和火箭的初始状态和最终状态有关，是不会和火箭的工作方式及过程有半毛钱关系的。以上的结论可以很容易的从齐奥尔科夫斯基公式中得出：

我还可以通过计算证明末速度和火箭的工作方式及过程的无关性，以下就是和高考题答案的讨论方法完全一致的情景，只不过计算利用了齐奥尔科夫斯基公式：

到这里我就陷入了无比的纠结，完全不同的两种结果！！我第一个想到的突破口是利用火箭最终输出的机械能比较来解决问题。因为我对火箭的基本假设（认识）之一是：对于一台已经确定了的火箭发动机，那么它最终输出的机械能就会唯一确定。很明显，以上假设与齐奥尔科夫斯基公式是相符的。所以我认为答案的计算过程有误，就按照同桌的建议用特殊值初略的分别计算了一下法一和法二火箭所输出的机械能（本来我是打算全保留字母推导的，不过这样就带来了超级大的计算量，会让人发疯的！）。最后在教室电脑的帮助下（即使用特殊值法，计算量还是大得惊人，无奈只能趁下课的几分钟占用了一下电子教学平台）得到了一个让我惊讶但又好像情理之中的结果：法二火箭输出的机械能比法一的多！！这就让我更纠结了，这道题把我的“火箭观”给颠覆了！！

接下来我基本一周的时间都卡在了这（基本每天都两节课+晚睡一小时去想。。。），想了很多种可能和物理定律，具体我也说不清楚了，反正之间的一切YY和纠结都用下面这张图来表达吧（这些都是在高考题的假设上的思考）。。。

一周，YY了这么久，最终还是一无所获。。。但我始终认定答案是错误的，不过是我对这些“教科书”上的东西早就没有了信任。不过撞了这么多次墙，我也慢慢冷静了下来，开始整理我之前的思路：我一直都在高考题给定的基本假设的基础上试图证明结论是错误的，但很明显到目前为止的证明都无法找出错误点或矛盾的地方。在这一周的证明过程中我还发现了一个奇特地方：按照高考题给定的基本假设推导得出的任何结论，都与利用齐奥尔科夫斯基公式以及我对火箭工作的基本假设推导得出的任何结论没有交集，反之亦然！！似乎这是两个宇宙，它们所遵循的物理规律是不一样的！！当然这是不可能的，但如果我继续坚持高考答案是错误的，那问题的根源就很清楚了—— 高考答案的基本假设一定是错误的！！

而且当我再一次使用特殊值验算（这次特地也用齐奥尔科夫斯基公式算了末速度，上一次并没有这么做）的时候又有了一个巨大的发现！！用三种方法算出的末速度，它们的大小关系竟然是：

这里似乎暗示了某种可能：在相同的燃料质量和相同喷出的相对速度下，抛出的小球（燃料）个数越多，那火箭的末速度就会越大，而且火箭的速度上线还很有可能就是V齐！于是在兴奋中我把高考题答案的讨论方法推广到了一般情况（由答案中的算式结构很容易得出）。

假设燃料的总质量为 N，并平均分为 n 次向后以相对于火箭的速度 v 喷出，且火箭空壳的质量设为 M ，根据伽利略的相对性原理，火箭的最终速度 Vm 为：

上面的上下两条式子是一样的，不过是上面的式子更容易理解，下面的式子表达更简便罢了。怀着异常兴奋的心情，接下来就是把 Vm 算出来了。可以看出来，上面的式子是一个数列的求和过程，Vm 就是这个数列的所有项数之和，而且这个数列类似于“一个等差数列的倒数形式”，也就是{1/1,1/2,1/3，..，1/n}

的形式。这是我没学过的，更是无法解决的，无奈只能先放下了（不要问我为什么不去问老师，1.和“教科书”一样，我对某些科目的老师在学术上的信任度是基本为零的。2.拿这种课外问题去问，人家是绝对不会理你的。），等周末回家上网查查看解决方法再说吧（不知不觉已接近周末）。。。

在等待周末的一小点“空余时间”里我又YY了一下：我之前一直都是在高考题的假设内讨论（毕竟我目前学的就是这些东西，很熟悉），而另一边（齐奥尔科夫斯基公式）却是一片空白，因为甚至我都不知道齐奥尔科夫斯基公式的基本假设是啥，更不知道公式的推导方法和过程。所以打算周末回去也顺便上网了解一下齐奥尔科夫斯基公式的推导过程，很难说这是不是自不量力。。。

然而，上图就是我查找几个小时后唯一的的结果（毕竟回家的时间不多），更别说齐奥尔科夫斯基公式的推导过程更是连影子都没看到（本来还想推导过程看不懂的话就买一本高等数学基础先学习一下）。。。谁说天无绝人之路的。。。那以后我一直在感叹老天真是不公。。。看来解决这道奇题的希望是彻底破灭了。。。

时间来到了下一周，星期一综合征加上是节超级无聊的化学课，为了不让自己睡着，我又拿出了那道高考题，盯着之前自己推出来的火箭末速度公式发起了呆（或者说是陷入了思考）：“如果n的值... ...”。。。对啊！！那样的话就可以用微积分去解决了！！我又看了一遍那道公式，一下子困意就全部消失了，马上就拿起了笔，不到半节课齐奥尔科夫斯基公式就出现在了我的推算过程的最后一个等号后面！！当时那个兴奋劲，那个激动！！真的无法形容啊！！（或许可以，Two Steps From Hell - Victory 网易音乐 XXXXXXXXXXXXXXXXXXXX/#/song/31654455 就是这首曲子，就是胜利啊！！）如果不是就坐在讲台下面控制住了，那会儿还不知道会怎么疯。。。（其实不止半节课，不过半节课推导的骨架确实完成了，还花了点当天的其余时间做了些补充）

下面应该就是这篇帖子的重点了——我自己推导齐奥尔科夫斯基公式的过程。现在看来整个过程不过是高二的数学水平，亏我当初还高估了它，以为得利用高等数学去解决。考虑到科普贴为了尽可能让更多人看得懂，所以下面说的可能会有点啰嗦，请大神勿拍。。。

回到我上面的得到的那个公式：

假设燃料的总质量为 N，并平均分为 n 次向后以相对于火箭的速度 v 喷出，且火箭空壳的质量设为 M ，根据伽利略的相对性原理，火箭的最终速度 Vm 为：

仔细点来说，对这里 Vm 的含义就是当 N Kg燃料平均分成 n 份，当 n 份全部分别以相对火箭的速度 V 抛出后，火箭的最终速度，而且当抛出第 i 份后火箭将获得一个 Vi 的速度增量（也就是最上面那条式子每两个“+”之间的部分）。

虽然 Xi 的取值是分立的（正因为如此我最初才希望利用数列去解决），不过可以利用微积分的思想，即：当 n 趋向于无穷大时（即当燃料被分成无穷多份），那么每个 Xi 之间的差量将变得非常小，以至于可以忽略，那这时 Xi 的取值就是连续的了。现回到火箭的真实工作状态：火箭向后喷气是一个连续的过程，那以上的假设就和真实火箭连续的实际工作过程是一致的。

那么f（x）在[0，N]上就是一条连续的曲线了，因为是一条连续的曲线，所以就可以用微积分定义来求解 Vm 了。接下来假设下图为f（x）在区间[0，N]上的图像（假设图像是为了方便大家理解推导过程，具体真正的图像是什么样的并没有实际意义）：

由前面的讨论我们已经知道了，Vm 应该就等于f（x）在[0，N]上 y 的所有取值之和，但直接求解显然是不可能的。所以在这里我同样是利用微积分的思想去解决。同样设区间[0，N]是由 n 个片段组成的，所以就把整条连续的曲线平均分成了n份，那每份区间的长度就为 N/n ，同时这样也将在[0，N]上由曲线f（x）与坐标轴围成的阴影面积分成了 n 个矩形，每个矩形的宽为 N/n ，高就为f（Xi）=Yi，如图：

之前的最后一步犯了低级错误，S2的V写漏了，经坛友指出，以下是改正后的过程：

到这里，推导过程就结束了，特别说一下我为什么用极限法的原因：很明显整个推导的源头是一个数列的前 n 项和公式，那极限法就是唯一能走的路了（这之后，我其实尝试过用一般的过程推导，不过那时候没成功）。有意思的是，在这里齐奥尔科夫斯基公式竟然是在高考题的答案中演变出来的，这里就可以看出他们还是互通的，只不过齐奥尔科夫斯基公式是动量定理的一种特殊情况，但是重点就是这里，这也是高考题的基本假设为什么错误的地方！

从齐奥尔科夫斯基公式的整个推导过程就可以看出，齐奥尔科夫斯基公式的基本假设是：燃料分为无数多份并以无数多次的或连续喷出（这个假设自然是符合火箭的实际工作状态的，因为火箭的工作状态就是在一段时间内将燃料连续不断地向后喷出，每一瞬间喷出的燃料可以认为是零。这就像一辆匀速行驶的车，虽然车在某一瞬间被认为是静止或者说在那一瞬间车的位移为零，但很明显车在一段时间的运动后是有位移的，这样就可以说车在那一段时间内经历了无数个相同的瞬间，积累了无数个无限接近零的位移所得到的结果）后，火箭所得的最终速度。而高考题的假设是：火箭燃料以有限的份数并以有限的次数喷出（已知的所有火箭都不是这样工作的，这样火箭的工作状态将是不连续的）后，火箭所得的最终速度。

虽然这里的齐奥尔科夫斯基公式是由一个较为特殊的情况推出来的。不过随着齐奥尔科夫斯基公式的成功推导，那道让我纠结了一周多久的奇葩高考题自然也就解决了。

先要明确的是：当动量守恒时，一个确定的物体分裂为两个物体（质量分别为 a 和 b）相对运动时（和火箭想后喷气并向前运动是等价的），一旦 a 对 b 的相对运动的速度确定，那整个过程中释放的机械能就只与 a 与 b 的质量相差程度有关（或表达为与 a/b 或 b/a 与 1 的大小有关），且质量相差越大整个过程所释放的机械能也将越大（或表述为 a/b 或 b/a 的值越远离1整个过程所释放的机械能也将越大）。

那我们现在就分别深入了解高考题的假设和齐奥尔科夫斯基公式的假设之间本质的不同吧。

1.关于高考题的假设。前面已经提到过了，用答案的方法计算结果是法二释放的机械能（这里指燃气和火箭的总机械能）将大于法一的，这是违背事实的！从高考题答案的方法可以看出每次抛出小球时法一和法二的小球（燃料）和火箭的质量之比是不一样的：法一是 3m/M 而法二分别是 m/（M+2m），m/（M+m），m/M，法二每一次抛球时的质量之比都比法一的更远离 1，那自然由此算出的机械能输出量就是法二大于法一了。相同的系统，输出的机械能越大，火箭的末速度自然也就越大，而且因为是相同相等的燃料，既然输出的机械能都不相等，热效率也就不可能相等了。

2.关于齐奥尔科夫斯基公式的假设。而对于齐奥尔科夫斯基公式，它的计算的过程是连续的或者说是分为无数个小球抛出后的结果，因为被分成了无数份，那每一个小球的质量都无法再分，而且质量是非常小的。就因为每一个小球的质量已经小到了极限，所以每一次抛球时与火箭的质量之比已经最大程度的远离了 1 ，所以在这里每一次抛球，系统的机械能就已经得到了最大程度的释放！所以无论你以任何方式抛球，只要你抛出的球的总质量（燃料质量）是一定的，那火箭的末速度也就是确定的（而且 V齐 > V2 > V1 也就不难理解了），那么输出的机械能也是一定的了，自然热效率也就不变了。

从齐奥尔科夫斯基公式的基本假设我们还可以知道。既然火箭的末速度与火箭的工作过程无关，那要怎样提高火箭的末速度呢？从我在上面的讨论就可以知道了：

1.增加两个物体的相对的远动速度（气体喷出速度）以提高系统输出的机械能，以让火箭达到更大的末速度。（实际上就是增加发动机的比冲，比冲越高火箭的末速度就越大）

2.减少死重，增加燃料的比重，以便让机械能更多地向火箭积累，，而不是浪费在燃气的机械能上。

这两个增速方法虽然是从齐奥尔科夫斯基公式的基本假设中得到的，但是他们都可以在齐奥尔科夫斯基公式中完美的体现出来，再次证明了推导过程的正确性！！

到这里，那道高考题的可笑程度就暴露无遗了，不知道出题人是怎样想的，竟然出了一道违反事实的题目（不过在我的上学经历中这种事算是常见的吧，也直接照成了我现在对“教科书”的“不信任”，不过这种严重的程度还是第一次见）：

我又回来看了一下这道题，它的致命伤是把连续喷出的气体当成了一整块的刚性小球，通过上面的讨论这两个模型是有本质区别的。而且发现这明显就是张冠李戴。“这道题目前面的那一堆科普“废话”都是事实，然后出题人就以他那毫无火箭常识的脑子加一点皮毛的动量知识，凭空YY出了一个看似符合事实的伪命题，竟然还让我帮他证明这是成立的！”—个人意见。。。而真正的多级火箭增速原理应该是上面讨论的第二种加速原理，通过不断地剔除死重，可以增加燃料的比重到一个很高的水平，这样就可以大幅度的提高火箭的末速度了。

帖子到这里也要结束了，有意见或问题尽管提（下一帖恐怕也是半年之后了）。想想高考复习半年过去了，唯一的兴趣也就这一点了，真是太空虚了，不过也没办法，高三就是不能玩也不敢玩啊，目标还没有达到，继续努力学习吧[s:328][s:328]

[修改于 8年4个月前 - 2016/08/10 11:48:50]

加载全文

来自：航空航天 / 喷气推进