物理竞赛基础技能,LZ可以去搞搞物竞。
旋转体的推导都是类似的。LZ可以总结下规律。
我们的征途是星辰大海,纵使前方是一望无际的黑暗森林。——写在前面
本帖子将推导极细圆环,球壳,球体,实心圆柱,薄管,旋转椭球体,圆锥体的转动惯量计算公式。


20200308更新
偷个懒,有些东西没推,直接写个计算器,要用自己带数算去。
这个计算器我估计一看就明白,有不明白的问就行、
转动惯量计算界面

半圆弧生成器

冯卡门曲线生成器

计算器(在WPS2020调试通过,欢迎转载,欢迎改进)
[修改于 4年9个月前 - 2020/03/08 17:57:31]
先来转轴垂直于圆环所在平面且过圆心的极细均匀圆环的推导。
根据转动惯量定义显然有
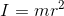
然后是极薄管子,转轴为管子的轴线,那么显然也有
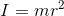
转轴过轴线的实心圆柱:把他拆成若干个半径为x,厚度为dx的管子,每一个管子的质量是
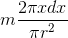
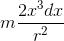
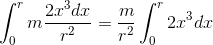
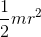
转轴过轴线的均匀圆盘同理,一巴掌拍扁圆柱(形象比喻而已)就是圆盘啊
别的改天再推。
L=mr2
KC的编辑器支持输入公式的,楼主可以尝试用公式编辑器去编写公式
我们不难发现,均质实心圆柱的转动惯量和质量相同、半径等于圆柱底面半径的均质薄圆盘的转动惯量相等...也和转动轴相同,高相同,底面半径和底相同的均质矩形转动惯量相等...
根本没法看,用mathtype编辑公式,粘贴进编辑器。或直接使用latex编写。
根本没法看,用mathtype编辑公式,粘贴进编辑器。或直接使用latex编写。
直接在编辑器里写LaTeX,公式一经插入,很难再次编辑。
还是先在LaTeX文档里写好或者用MathType吧。。
m∫r0r3dr∫r0rdr=12mr2
均匀圆盘这么积也行
\[\frac{{m\int_0^r {{r^3}} dr}}{{\int_0^r r dr}} = \frac{1}{2}m{r^2}\]
还是有好多bug,在公式编辑器里可以正常显示的公式确认之后就原形毕露了(直接从MathType复制过来的)。还有在编辑器中好好的公式发表文章就变成下面的样子:
m∫r0r3dr∫r0rdr=12mr2
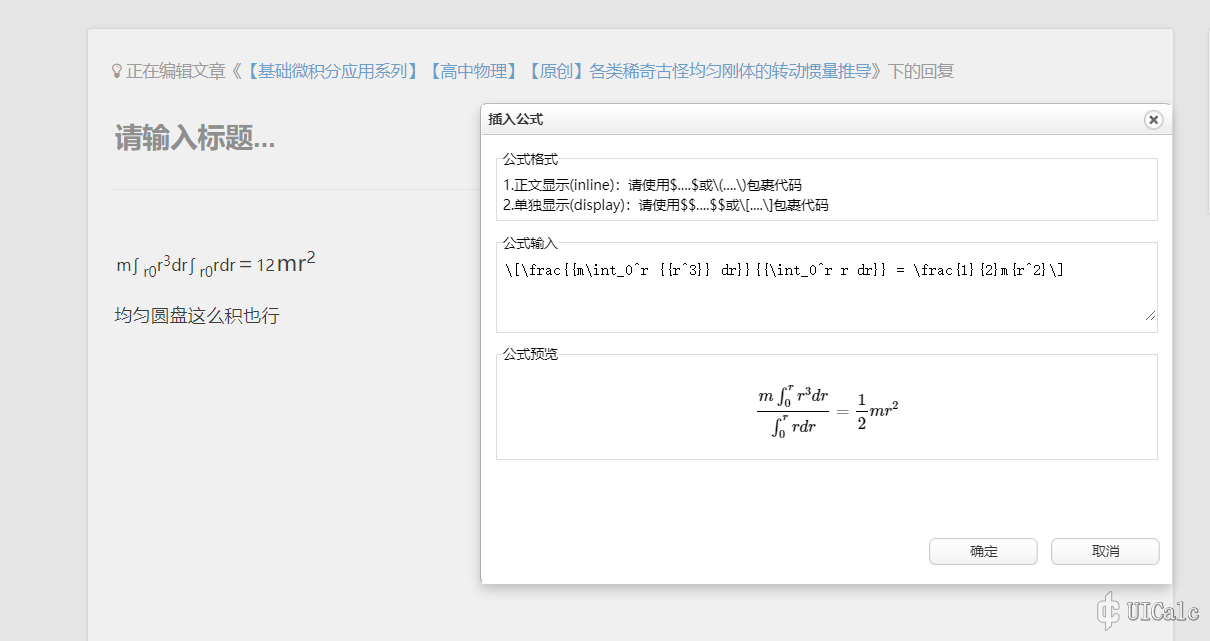
嗯?正常了。可能是浏览器插件加载的问题吧
@UICalc@虎哥@OliverKung 好吧 以前从来没用公式编辑器,我还得老老实实学习咋用。
话说我在我创发这个帖子纯粹班门弄斧,关公面前耍大刀。UICalc把我吊着打。
XXXXXXXXXXXXXXXXXXXXXXXX/latex/XXXXXXXXXXXXp?lang=zh-cn
我直接用着上面这个链接编辑的公式。
还行,图片直接复制过来稍稍有点模糊。
LZ初中生,把微积分学到这种程度已经很不错了~
深感惭愧,我连转动惯量都不知道是啥,只知道力矩Fr=mω2r2,微积分知识也只到泰勒级数(多元函数的全微分方程和偏微分方程都不会),《固机设计》也只是草草的看到《燃烧室设计》那一章,我是不是要凉了2333
高中物理学(竞赛版的,四本),高中数学课本,高中物理课本。
高中物理学比教材编得好,适合作为竞赛基础知识。微积分弄本大学教材,比如同济的蓝皮哪本,物理竞赛不用太深会点微分方程就行了(竞赛题目基本都可以通过代数式的处理求解)。要刷题就去黑白皮,程稼夫之类的
懒得打字了,发图:均匀球壳与球体的,转轴过球心。现在推的几种都有mr2项,看看啥样的有。估计常见旋转体都满足这一规律吧。

你们是要抛物旋转体和冯卡门曲线的推导呢,还是要旋转体转动惯量计算器呢?哪个对你们的作用更大?
本帖在我严重偷懒的情况下胜利完工(有本事顺着网线咬我呀


噢哟,我竟然晚来了靠。
先赞为敬!!!棒!!!


| 时段 | 个数 |
|---|---|
| {{f.startingTime}}点 - {{f.endTime}}点 | {{f.fileCount}} |
200字以内,仅用于支线交流,主线讨论请采用回复功能。