光说不练从来不是科创的风格,下面讲一讲 Logistic Regression 的程序实现和实验。
在实验中我使用 Python,在 scientific computing 上,Python一直是主流,机器学习也不能免俗,而 numpy 提供的便捷的向量化运算,给诸多机器学习的算法实施提供了便利。另外强烈推荐ML新手装 sklearn 这个package。
导入库:
import numpy as np
from numpy import linalg as LA
import matplotlib.pyplot as plt
import sklearn.datasets
import sklearn.cross_validation
以下是计算梯度的函数,使用了numpy的向量化计算特性:
def calculate_gradient(w,x_batch,y_batch):
sigmoid=1/(1+np.dot(x_batch,np.transpose(w)))
dL=np.dot(sigmoid-y_batch,x_batch)/y_batch.size
return dL
计算Loss function,注意,数据溢出是Logistic Regression程序实现的一个主要问题,因为exp函数的输出,用float 表示时,实际上输入被限制在[-750,750]这个区间内,不做处理的话基本上肯定会上溢。这个问题的解决同样在这本书中有讲:
def calculate_loss(w,x_all,y_all):
### Avoid Overflow! ###
pos_index=np.where(y_all==1)
neg_index=np.where(y_all==0)
Loss=np.sum(-np.log(1+np.exp(-np.dot(x_all[pos_index,:],np.transpose(w)))))+np.sum(-np.log(1+np.exp(-np.dot(x_all[pos_index,:],np.transpose(w)))))
return Loss
训练过程主循环,注意对learning rate采用了annealing,在SGD过程中分段一点点减小步长,不然很容易最后变成在global minimum周围反复徘徊难以收敛:
def train(x_train,y_train,alpha,batch_sz,loss_thresh,Max_iter,w0):
### bias trick ###
w=w0
data_sz=y_train.size
x_train_b=np.concatenate((x_train,np.ones((data_sz,1))),axis=1)
Loss_old=0
Loss=[]
stepCnt=0
### Run SGD ###
for iter in range(1,Max_iter):
### sample a mini batch ###
batch=np.arange(data_sz)
np.random.shuffle(batch)
x_batch=x_train_b[batch[:batch_sz],:]
y_batch=y_train[batch[:batch_sz]]
### update weight ###
dL=calculate_gradient(w,x_batch,y_batch)
w-=alpha*dL
### record loss changes ###
Loss.append(calculate_loss(w,x_train_b,y_train))
### learning rate annealing ###
stepCnt+=1
if stepCnt==10:
stepCnt=0
alpha*=0.8
### Check if converge ###
if abs(Loss[-1]-Loss_old)<loss_thresh: break loss_old="Loss[-1]" return w,loss < code></loss_thresh:>
使用了sklearn的数据生成函数,之前的图表数据皆来源于此:
def make_data():
centers = [(-10, -10),(10, 10)]
x, y = sklearn.datasets.make_blobs(n_samples=2000, n_features=2, cluster_std=5.0,
centers=centers, shuffle=False, random_state=100)
x_train, x_test, y_train, y_test = sklearn.cross_validation.train_test_split(x, y, test_size=.4)
return x_train, x_test, y_train, y_test
主函数,w被初始化为全零向量,mini batch size 是50 :
def main():
alpha=0.5
batch_sz=50
Max_iter=2000
loss_thresh=1e-5
w0=[0,0,0]
x_train, x_test, y_train, y_test = make_data()
w,Loss = train(x_train,y_train,alpha,batch_sz,loss_thresh,Max_iter,w0)
plt.plot(Loss)
以下是记录的学习过程中 Loss function 的收敛过程。
![output_9_1.png]()
得到的w的值为[ 123.01618818 125.42445694 11.78221087]。
画成直线可以看出,跟理想情况非常近似
![result.png]()





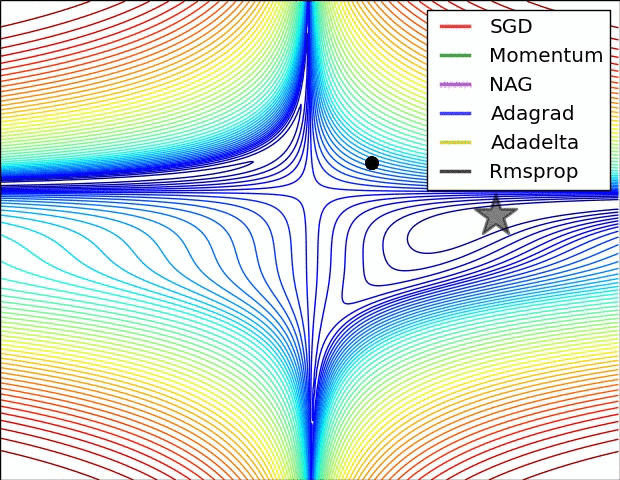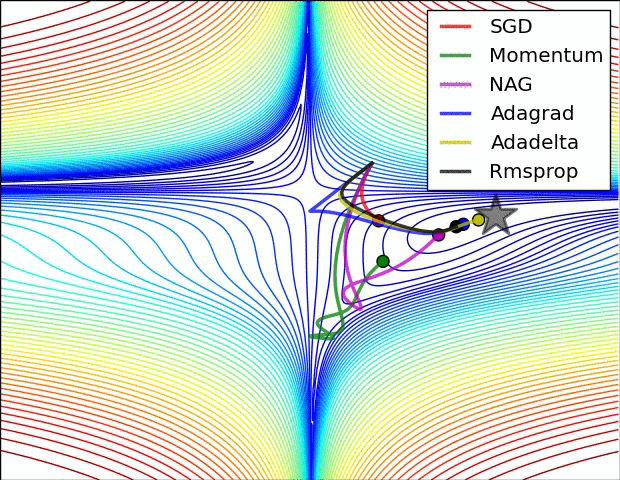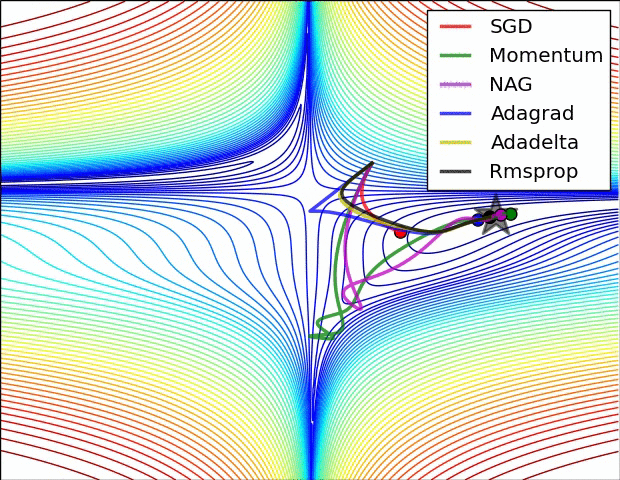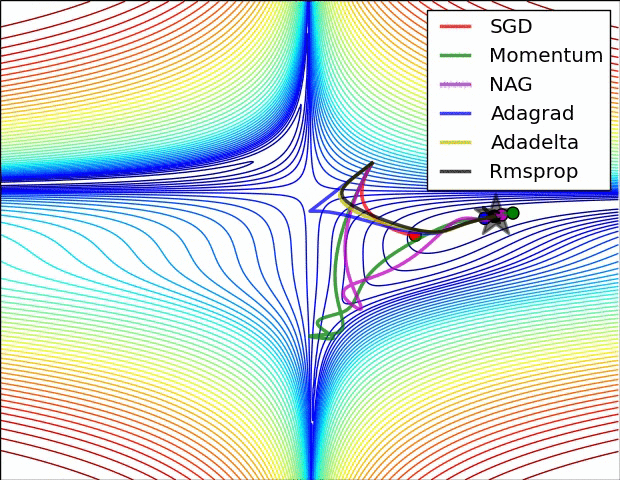


200字以内,仅用于支线交流,主线讨论请采用回复功能。