拿到了\(L(w)\)的表达式，下面该如何找到正确的w，使得\(L(w)\)最小呢（注意，求最大变成了求最小）？

祭出凸优化中神挡杀神，佛挡杀佛的梯度下降法（gradient descent）。



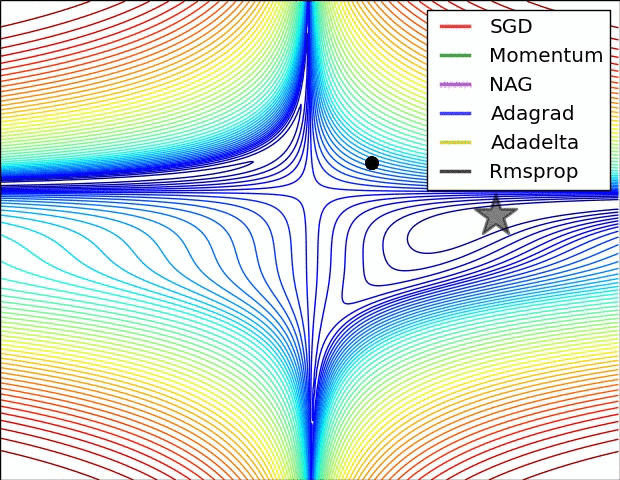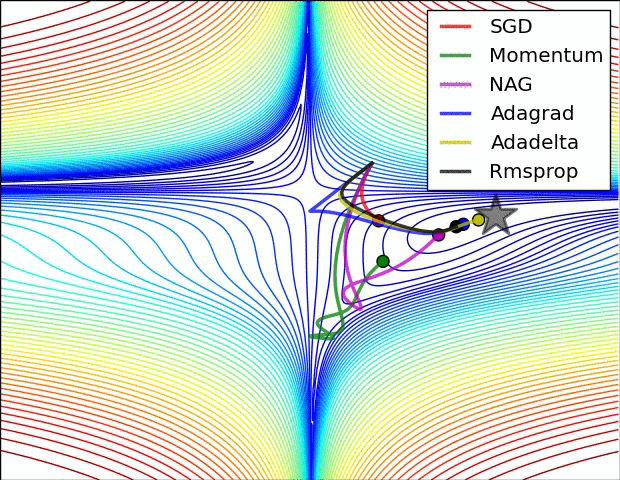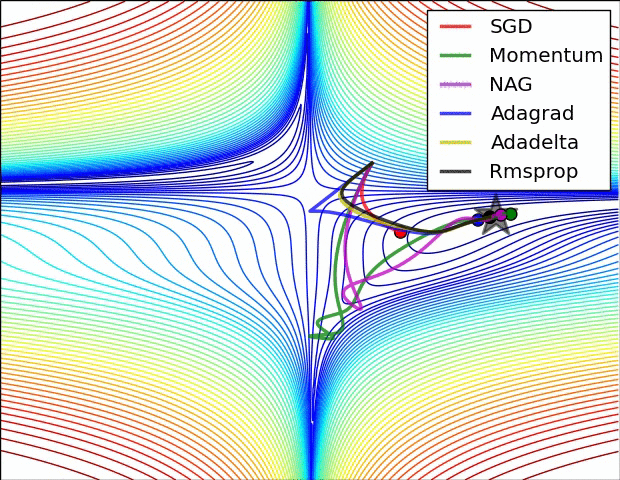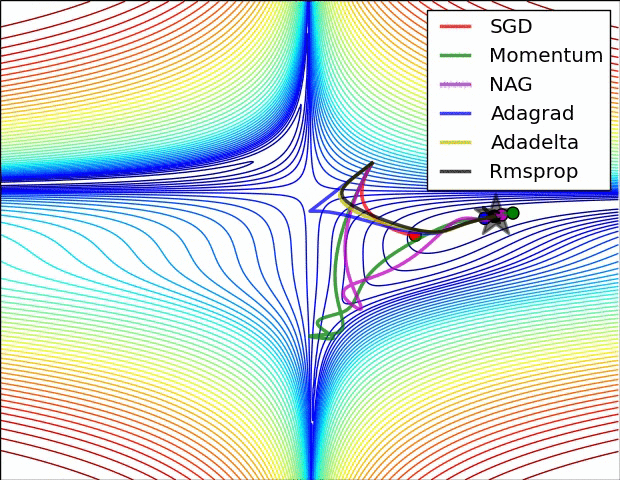
图片来源
思路简单说就是，虽然我不知道w取坐标轴上什么位置好，但我可以一小步一小步的挪过去，每挪一步都向着当前所在位置坡度最陡的地方去。于是我们就这样慢慢的圆润的滚道谷底了。

可以证明，“坡度最陡”的方向，就是该点导数方向的反方向，这本书的这个章节有极好的详述。于是我们要对\(L(w)=-\sum_i log(h(w^Tx_i)^{y_i}(1-h(w^Tx_i))^{1-y_i})\)求导：
$$\frac{\partial L(w)}{\partial w}=\sum_i (h(w^Tx_i)-y_i)x_i$$ 得益于sigmoid函数良好的求导特性和log函数的特性，这个导数表达非常简洁。

在实际程序中，我们只需要算出每个数据点对应的\((h(w^Tx_i)-y_i)x_i\)，然后求和，就能得到当前w的导数表达。

但是这样真的好吗？

首先训练集的数据量一般都非常大，达到成千上万的地步，对如此大的数组频繁反复求和从计算的角度讲是非常不利的。其次，更重要的一点，我们无法保证整个数据集的数据都是有效数据，其中必然包含噪声，而把这些噪声算入我们每次计算的导数中，是非常危险的。

于是，这里我们使用另一个思路（所以我觉得机器学习里边的方法论实在是占据太多地盘了。。），每次求导时从整个数据集中随机抽取一小部分数据，用这一小部分数据作为样本来计算导数

这就是在各种机器学习算法中一路通杀的大名鼎鼎的 stochastic gradient descent，简称SGD，这种形式也叫 mini batch 法。无论是简单如Logistic regression，还是复杂如深度学习网络，优化思路基本上都是用SGD，或者说没有脱离SGD的模子。