在日常生活中，我们可能会遇到像导航路线选择的问题.这时我们就需要从诸多路径中选择最短的一条.

为了解决此类问题我们需要引入一个概念——图.

（图-1）

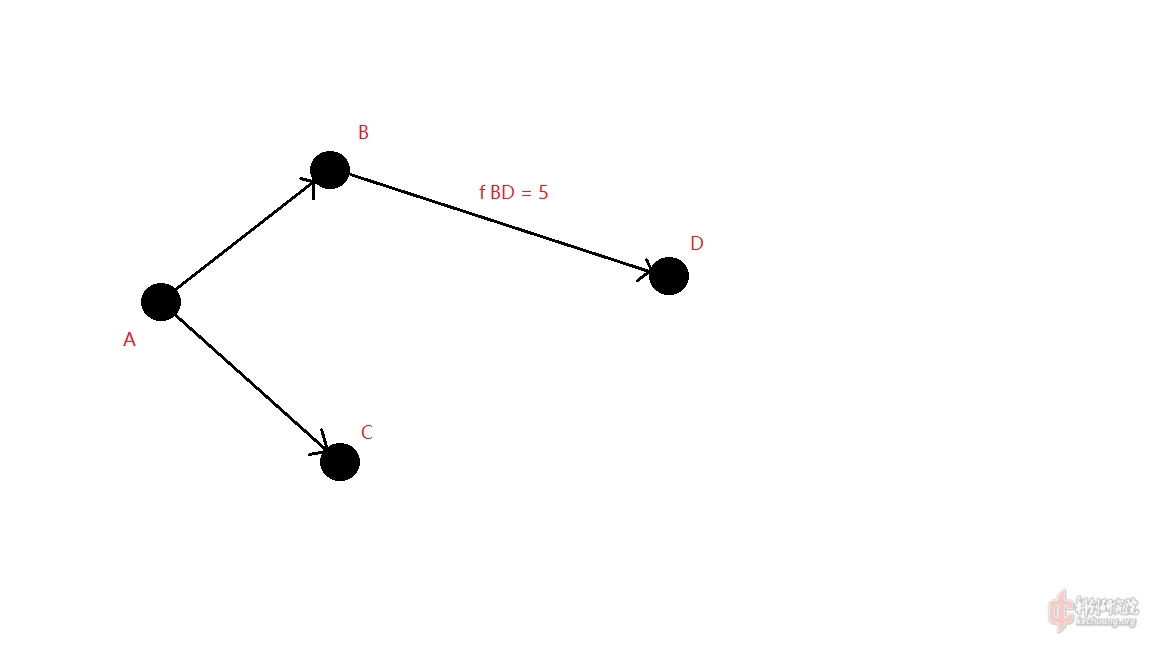
如图-1，这就是一个图.图中的每一个节点叫作顶点，连接两个顶点的线段叫作边.当然，有一些图中由顶点指向顶点的边是有向的（比如该图）叫作有向图，也有的图由顶点指向顶点的边是无向的叫作无向图.图中的每一条边都可以有一个权值$f$，比如图中BD边的权值就可记作$f_{BD}=5$.

若将图描述为一个集合$G$,那么则有

$$\begin{gathered} V,E\subset \\ G \end{gathered}$$(1)

其中$V,E$分别为点集和边集，他们都是$G$的子集.

尽然了解了图的概念，我们将讲解一下Dijkstra算法.

参照百度百科对Dijkstra算法的介绍：迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有权图中最短路径问题.迪杰斯特拉算法主要特点是从起始点开始，采用贪心算法的策略，每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止.

设带权图$G=(V,E)$,求v到其它点的最短路径.开一个二维列表Weight作为边的权值，d[i]为点的值（初始为无穷大）.sign[i]为标记列表,数值类型为bool,初始为False.

大致步骤如下：

1. d[v] = 0,sign[v] = True

2. 对当前已确定的点i，寻找所有未确定的点j，若边<i,j>存在则进行松弛操作d[j] < d[i] + Weight[i][j]

3. 确定i和d[i].即对所有为未打上标记的点j，枚举找出最小的点d[j],令sign[j] = True.

   重复2、3步骤直到所有的点都被确定为止.

   显然，理想情况下上述算法的时间复杂度为$O(n^2)$

   以下是我用python编写的测试代码：

Python
开启自动换行复制
import openpyxl
import heapq

def read_graph_from_excel(filepath):
    workbook = openpyxl.load_workbook(filepath)
    sheet = workbook.active
    graph = {}
   
    for row in sheet.iter_rows(min_row=3, values_only=True):  # Start from row 3 now, since we skip the first two rows
        node1, node2, weight = row[0], row[1], row[2]
        if node1 not in graph:
            graph[node1] = []
        if node2 not in graph:
            graph[node2] = []
        graph[node1].append((node2, weight))
        graph[node2].append((node1, weight))  # Assuming an undirected graph
   
    return graph

def dijkstra(graph, start):
    distances = {vertex: float('infinity') for vertex in graph}
    distances[start] = 0
    pq = []  # Priority queue
    for neighbor, weight in graph[start]:
        heapq.heappush(pq, (0, neighbor))  # Set initial distance to 0 for neighbors of start node
    while pq:
        current_distance, current_vertex = heapq.heappop(pq)
       
        if current_distance > distances[current_vertex]:
            continue
       
        for neighbor, weight in graph[current_vertex]:
            distance = current_distance + weight
           
            if distance < distances[neighbor]:
                distances[neighbor] = distance
                heapq.heappush(pq, (distance, neighbor))
   
    return distances

# Read the graph from Excel
file_path = r"C:\Users\Administrator\Desktop\new1\s.xlsx"
graph = read_graph_from_excel(file_path)

# Run Dijkstra algorithm
start_node = 1  # Change this to match the first node in your Excel file
distances = dijkstra(graph, start_node)

# Print the results
for node, distance in distances.items():
    if node != start_node:
        print(f"Shortest path to node {node}: {distance}")

程序保存在C:\Users\Administrator\Desktop\new2目录下的s1.xlsx文件作为输入（不知道为啥我一用相对路径就报错，所以我选择了绝对路径），xlsx文件的A列用来保存原顶点，B列用来保存与其连接的顶点，C列用来保存权值.测试的图如下：

（图-2）

结果为

Python
开启自动换行复制
Shortest path to node 2: 3
Shortest path to node 3: 6
Shortest path to node 4: 5
Shortest path to node 5: 7
Shortest path to node 1: 2