厉害!收藏了,学习下,我准备做声呐了
合成孔径算法简介:
前置知识:雷达原理:脉冲压缩/匹配滤波:XXXXXXXXXXXXXXXXXXXXXXXX/t/81629
有关孔径和合成孔径:
对于通常的(真实孔径)的成像装置而言,在波长一定的情况下,孔径越大,其角分辨率也越大。
假设这是成像装置的”孔径“,无穷远处的某种波(光波/微波/声波……)以单色平面波的形式与成像装置孔径平面成夹角入射到其上,那么显然,成像装置上不同位置收到的波相位是不同的,类似这样:
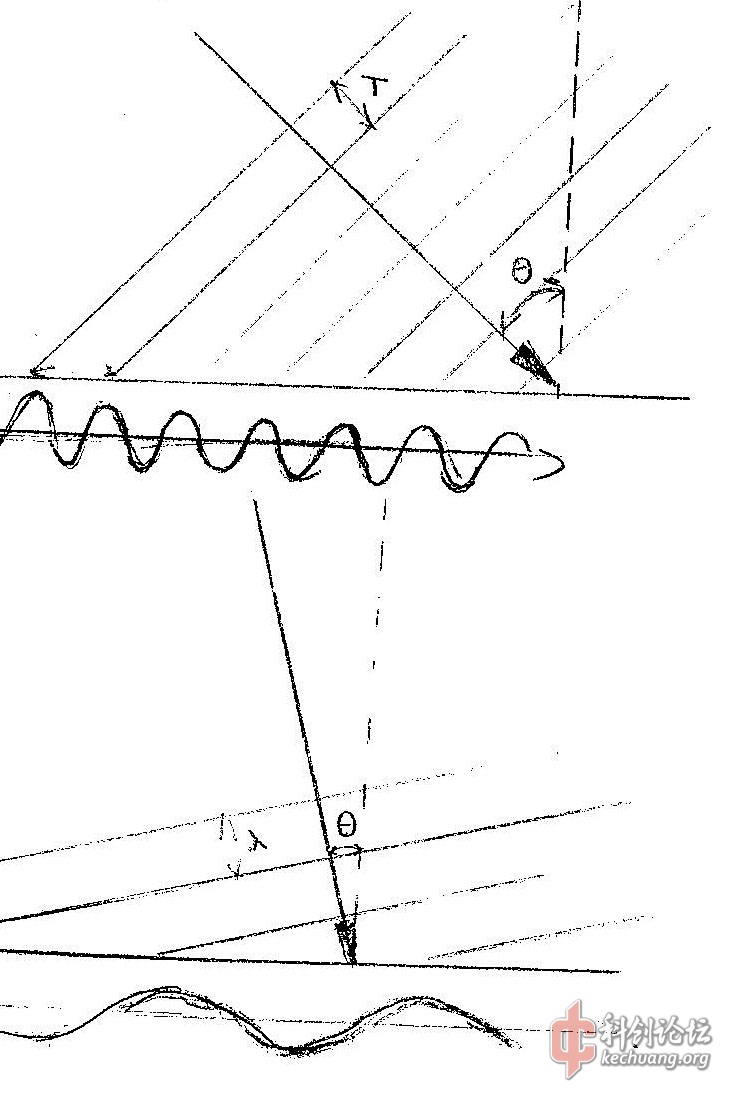
成像装置上形成了波纹,而入射波的入射角越大,波纹的空间频率(波数)也越大。不同的空间频率对应了不同的入射角度。
无论是干涉式成像或是透镜/抛物面反射镜成像,其成像的过程都可以描述为对在成像装置上收到的波进行二维傅里叶变换,求出”波纹“的二维频率(波数),也就是入射的角度。

由傅里叶变换的性质可以得到,傅里叶变换的长度越大,频率分辨率越小(高)。到这个例子上来说,就是成像装置的孔径越大,成像的角分辨率越高。当然同时入射的波波长越短,能达到的频率范围也越大。因此这种情况下角分辨率的计算公式和孔径成反比,和波长成正比:
$$ \frac{1.22\lambda}{D}$$
为了获得更好的分辨能力,提高孔径大小就成为了制造成像装置的目标之一。但是单个成像装置的物理孔径大小总有各种各样的原因限制,因此需要有其他的方法增大孔径。例如可以使用分布在不同位置的多台成像装置同时工作,通过干涉来形成一个较大的成像孔径。对于雷达而言,由于信号本身是自己发出的,其各个时间的信号参数已知,可以使用移动雷达,在移动过程中连续在不同时间不同位置进行成像的方法,“合成”出一个较大的孔径。

如图,雷达在移动过程中照射目标,从目标开始被波束照射到目标照射结束的时间内雷达移动的距离即为合成孔径。定性地来看,对于距离远的目标,虽然视角较小,但合成孔径大角分辨率也高;对于距离近的目标,虽然合成孔径较小角分辨率也较低,但视角大。总的来说在不同距离上的方位向分辨率是一样的。
方位向分辨率:
$$ \frac{0.886\lambda}{2\beta} $$
$\beta$为波束宽度
同时也可以看出,如果天线本身的增益越大,波束越窄,反而合成孔径越小,分辨率也越低。和通常的真实孔径雷达恰恰相反,这是合成孔径雷达比较奇特的一个特点。
算法推导和仿真:
算法推导所必要的一些假设:
假设地面为一平面,目标分布在地面上。
雷达在地面上一定高度h沿着平行于地面的方向进行直线运动,间隔一定的距离发射一次脉冲。
在任一时刻,垂直于雷达速度矢量并过雷达的平面上的目标相对于雷达的径向速度为零,因此多普勒频偏也为零,此平面称为零多普勒平面。
雷达收发天线波束中心的方向指向雷达速度矢量的一侧(左/右)并对着地面,波束中心方向可以不与零多普勒平面重合,波束中心方向与零多普勒面的夹角称为斜视角。与 雷达速度方向矢量相同的方向称为方位向,向收发波束一侧,与地面平行且与雷达速度方向垂直的方向称为距离向。
在任一时刻,雷达到目标点的距离为斜距,而运动过程中,雷达正下方地面上的点到目标的最近距离称为地距。
由于雷达运动的速度$v$相比于雷达信号前进的速度$c$可以忽略不计,因此推导时可以近似看作雷达每次前进一段固定的距离,发出发射脉冲,在“原地”就收到了相应的回波信号。(“走-停假设”)
回波信号的推导和成像仿真:
首先,假设单次发射信号为线性调频信号,带宽为 $Bw$ ,脉冲长度为时间$T_s$,则调频率$k=Bw/T_s$。则单次发射信号的表达式(基带)可写作
$$ s(t)=\exp( \pi jkt^2){\rm rect}(\frac{t}{T_s}) $$
此信号经过上变频到中心频率为f的高频上发射。为了避免信号两端截断带来的频谱泄漏,发射信号通常还需要加窗,这里为了方便,直接使用矩形窗。对于目前“瞬时”斜距为r的点目标来说,对应的单次回波信号在基带上看,相比发射信号产生的延时等于飞行时间
$$ T=\frac{2r}{c} $$
同时由于实际上在空中飞行的是中心频率为f的高频信号,因此产生的相位延迟是
$$p=\frac{2\pi f}{T}=\frac{4\pi fr}{c} $$
因此单次回波信号的基带表达式可以写作:
$$ r(t)=\exp(\pi jk(t−T)^2−(2\pi jfT)){\rm rect}(\frac{t-T}{T_s}) $$
此时可以通过脉冲压缩将单次回波信号压缩成窄脉冲,其脉冲宽度为目标的斜距分辨率,可以由脉冲压缩相关的公式推导得到,约为
$$ \frac{0.886c}{2Bw} $$
经过匹配滤波,被压缩的脉冲信号的相位仍与原信号保持一致。即与发射信号保持了
$$p=-2\pi fT=-\frac{4\pi fr}{c}$$
的相位差。
多次雷达回波信号数据(基带)可以排列成一个元素为复数的二维数组(或者说矩阵),每行为一次发射脉冲所收到的回波数据,每行上的每个数据单元则是此次回波数据的每个采样点。多个这样的行沿着纵轴排成矩阵。横轴代表了回波的飞行时间(距离),称作距离向(或快时间维)。纵轴代表了雷达运动到的不同位置,称作方位向(或慢时间维)。

由于雷达在运动,所以每次进行采样时,雷达到同一目标的斜距会发生变化,称为距离徙动(RCM)。假设点目标地距为l,目标在速度方向上距离雷达的距离为x,则目标的瞬时斜距r则为$r=\sqrt{l^2+h^2+x^2}$,变一下形则是$r^2-x^2=l^2+h^2$可以看出是双曲线的形式。同时,目标相对雷达的径向速度也在发生变化,因此产生一个变化的多普勒频移,可以由径向速度推出或对上述相位偏差求导得出。为了推导方便,这里使用空间上的频率(波数)$\Delta f$(量刚为L-1),来代替多普勒频率的概念。多普勒波数(精确形式)
$$ \Delta f=\frac{1}{2\pi}\frac{\partial p}{\partial x}=-\frac{2fx}{c\sqrt{h^2+l^2+x^2}} $$
此偏移在目标通过零多普勒平面前为正,通过时为零,通过后为负。由此可以得到雷达回波信号(有三个不同位置的点目标)(仅显示实数部分,下同):

如图,可以看出RCM所产生的双曲线形状。雷达的回波数据不包含肉眼可以直接看到的目标,因此需要对其进行一些处理才能够进行成像。为了对目标成像,首先对回波数据使用距离压缩:

可见,回波在距离向上被压缩,宽度变窄,变为一条细双曲线。但是要怎么样进一步处理才能将数据在方位向上也压缩成点状呢?由上文可知,回波信号会产生多普勒偏移。虽然对于单个回波脉冲来说,由于单个脉冲相对于脉冲间隔极短,频率分辨率很大,而多普勒偏移相对于单个脉冲数据的频率分辨率可以忽略,因此在单个回波信号中不能直接检测到。但将多个回波信号排成矩阵沿着方位向观察,多普勒偏移产生的相位偏差就很明显了,同时这个相位偏差经过脉冲压缩之后仍然保留了下来。从方位向上看,多普勒偏移频率随着雷达与目标的相对位置变化,正逐渐变为负,类似于调频率为负的线性调频信号。所以能不能在方位向上对信号进行脉冲压缩呢?这样做会有一些问题:
首先,从上文中的推导和图像可以看出,雷达回波信号进行距离向压缩后并非一条平行于方位向的直线,而是一条双曲线,不能简单地在方位向上进行匹配滤波。
其次,方位向上的信号仅仅在目标接近零多普勒平面处可以近似为线性调频信号,对于较大斜视角的情况会产生较大误差导致压缩后的脉冲变宽。
因此:
需要使用一定的手段,消除RCM造成的影响,将双曲线变换为一条与方位向平行的直线,称为距离徙动矫正(RCMC)
在大斜视角的情况下,需要使用更精确的形式来代替线性调频信号推导匹配滤波器。
怎么进行距离徙动矫正?目前已经得到了各个采样时刻,目标距离雷达的瞬时斜距(即上图的细双曲线)。同时由上文可知,多普勒偏移是雷达到目标瞬时斜距和速度方向上距离的函数。
首先将距离压缩完成的回波数据在方位向上进行fft:

这样方位向轴就被方位频率(多普勒偏移)轴代替,因此变换完成后的域称作距离-多普勒域,这种处理算法称作距离-多普勒算法(RDA)。可以看到,由于雷达和目标在方位向上的距离越大,斜距也越大,径向速度和多普勒偏移同时也越大,在距离多普勒域中的点目标回波仍是一条双曲线的形状。
由之前得到的多普勒波数关系可以求解得出:地距为l的点,对应的多普勒空间波数为f的瞬时,雷达在方位向上和目标的距离
$$ x=\pm \frac{c\Delta f\sqrt{(2f+c\Delta f)(2f-c\Delta f)(h^2+l^2)}}{4f^2-c^2\Delta f^2}$$ 则瞬时斜距为
$$ r=\sqrt{l^2+h^2+x^2} $$
由于这个过程中考虑了高度h,可以直接得到地距(而不是最小的斜矩),也就是将RCMC和斜地配准在一步操作完成。
根据这个关系式,可以从矫正后数据中的对应点变换到相应矫正前数据的点对应位置上。由于变换之后并不一定是整数,而实际上的数据是离散的数组,数组下标只能是整数,因此通常还需要进行插值处理。这里偷懒直接强行四舍五入成整数,然后产生了一些不必要的花纹状噪音。不过还是很明显能看到轨迹变为了沿着方位向的直线:

完成RCMC后,对方位向进行ifft,变换回二维时域:

将此信号取复共轭并反褶后作为方位向匹配滤波器,对每一列进行匹配滤波(注意这个滤波器随着地距$l$变化,每一列用的是不同的滤波器)(为了效率可以在方位向ifft之前直接乘上这个匹配滤波器的频域形式)并取模长化为实数:

这样就将点目标的回波信号真正压缩成点状了。
实测:
由于合成孔径处理需要以模拟方式接收含有相位信息的回波数据,因此不能使用常见的超声波测距模块。这里使用单独的超声波收/发头(其实就是个压电扬声器)。
接受头收到的回波信号较弱,使用运放做一个1000-10000倍的放大电路将信号放大。单片机DAC的驱动能力较弱,需要使用运放放大后驱动超声发射头。整块收发电路:



发射信号使用带宽5kHz的chirp信号,脉宽约1ms。时间带宽积为5,经过匹配滤波可以压缩五倍。理论斜距分辨率为340/(2*5000)=0.034m=3.4cm
超声频率为40kHz,波束约有45度宽,理论方位向分辨率约为(340/40000)/(pi/4)=0.01m=1cm
最远探测距离设定在1.2m,该处回波发射后需要约10ms返回。再留出10ms将数据写入SD卡,脉冲20ms重复一次。
装到小车上:


小车后面的一大坨东东是为了配重,不然车头太重跑起来会翻。
摆好场景(此图和结果图中的左右是相反的):

由于小车用了两个独立的马达驱动轮子,同时又没有安装控制电路,因此运动过程中需要人力稍微调整才能按直线走。回波数据中有几处相位不连续由此产生。
原始数据(已下变频到基带,实数部分,下同):

距离压缩:

变换到距离多普勒域:

RCMC+斜地配准:

方位ifft:

方位向压缩(并取模长):

简单地来对比下效果:

成像效果很好,能够明显看出分立的目标,位置与场景中物体的摆放基本一致。不过由于小车速度不匀+超声收发头的实际响应带宽较窄的原因,分辨率没有达到理论值。
有关的代码:
STM32工程(STM32CUBEMX+IAR):
XXXXXXXXXXXXXXXXXX/gym487/STM32UltrasonicRADAR
仿真算法:
XXXXXXXXXXXXXXXXXX/gym487/SAR_exp/blob/master/XXXXXX
成像算法:
XXXXXXXXXXXXXXXXXX/gym487/SAR_exp/blob/master/XXXXXXXXXXXXX
实验得到的原始数据:
原始数据格式:每个数据为双字节定点数,小端序,每行4000个数据,共1000行。采样率500k,每行数据起始时间和发射数据开始时间同步,带有DC offset,需要去除后再下变频到基带。
发射数据是线性调频信号,采样率500k,长度512个采样。中心频率为40kHz,带宽5kHz,正扫频。运动参数见成像代码。
用法:按stm32cubemx中的引脚图连好电路并下载程序到stm32,插入sd卡,按下复位键,将开始自动发射接收超声信号并将数据记录入sd卡中。同时匀速直线运动装置,数据将记录20秒。SD卡中生成XXXXXXXn数据文件
将记录的数据文件XXXXXXXn和成像代码XXXXXXXXXXXXX放到同一个目录,可自行修改文件头部的参数,用python运行。稍等片刻可生成:
回波原始数据(基带) XXXXXXXp(实数部分) XXXXXXXXp(模长)
距离压缩后 XXXXXXXXp(实数部分) XXXXXXXXp(模长)
XXXXXXXXp 距离多普勒域(实数部分)
XXXXXXXXp RCMC后(实数部分)
XXXXXXXXp 重新变回二维时域(实数部分)
XXXXXXXXp 方位压缩完成的成像结果(模长)
XXXXXXXp 方位向匹配滤波器(实数部分)
仿真:直接用python运行XXXXXX,能够生成三个点目标场景的上述文件以及XXXXXXp地图文件,显示三个点目标的位置,用于和结果对照。
[修改于 6年3个月前 - 2018/08/29 08:42:07]
超声换能器可能有比较大的惯性(也就是Q值太高)。
这个帖子对许多爱好者可能难了一点,但长期来看会成为经典。雷达数据处理的软件过程,建议做一些说明,只放git可能吓跑小朋友。另外有没有考虑使用微波雷达原理来实现,目前24GHz的雷达芯片和模块已经比较成熟了,楼主可以设计一个方案,我们协助把它实现。
200字以内,仅用于支线交流,主线讨论请采用回复功能。
超声换能器可能有比较大的惯性(也就是Q值太高)。这个帖子对许多爱好者可能难了一点,但长期来看会成为经...
已补充有关代码的使用说明。
微波的方案也考虑过,不过我没有射频电路相关的经验,不太好做。。不过yy过几个方案:
方案一:使用现成的SDR平台收发,后面加上功放和收发切换开关,用PC+GnuRadio进行数据处理
实测我的渣笔记本同时带动USRP收发采样率超过10M就会在几秒内断掉并卡死,在略低的速率上也会出现严重的丢帧,例如这个是用同轴线+衰减器短接Tx/Rx口得到的“回波”数据的一段:

高速收发和处理需要高性能的PC,重量较重。但是微波版本的雷达成像范围和分辨率都大很多,理想的搭载平台是无人飞行器,较重的PC不容易搭载。而且用PC控制收发切换开关的话实时性不容易保证。这个方案放弃。
方案二:
使用9361+少量附加器件与FPGA开发板连接,由FPGA进行信号处理,顺便支持analog dechirp模式。
与极速外卖前辈交流过,感觉这个坑大得有点超乎想象,还是放弃了。
方案三(还没试过,不过应该是最可行的,但探测距离有点抓鸡):使用现成的Analog Dechirp方式的雷达模块,例如某宝上最便宜不到200大洋的这个:

FMCW模式距离速度探测 汽车>30米,人>15米 ,垂直对水泥地面>30米
Analog Dechirp方式由于将两路chirp信号混频,产生的回波相位除了与距离成线性的多普勒项,还有与距离成二次的Residual Video Phase项,算法需要多做一步处理消去。
Analog Dechirp方式的成像仿真代码:
XXXXXXXXXXXXXXXXXX/gym487/SAR_exp/blob/master/XXXXXXX
应该还有更远距离,容易实现的方案?
200字以内,仅用于支线交流,主线讨论请采用回复功能。
不说吹的, 某些研究生毕业论文都没这篇文章内容多,学习了.那个淘宝Ka波段雷达模组,有直接引出IQ通道吗
200字以内,仅用于支线交流,主线讨论请采用回复功能。
不说吹的, 某些研究生毕业论文都没这篇文章内容多,学习了.那个淘宝Ka波段雷达模组,有直接引出IQ通...
有,引出两路i/q可以用来在多普勒测速时判断速度方向。具体的话在某宝搜"fmcw"就能找到这类产品。
200字以内,仅用于支线交流,主线讨论请采用回复功能。
200字以内,仅用于支线交流,主线讨论请采用回复功能。
XXXXXXXXXXXXXXXXXXX/homemade-synthetic-aperture-ra...
感谢分享。这个方案还带有pll来修正vco的非线性,看起来比某宝上的模块靠谱不少。还有开源的设计文件提供,也许能山寨个类似的出来。
200字以内,仅用于支线交流,主线讨论请采用回复功能。