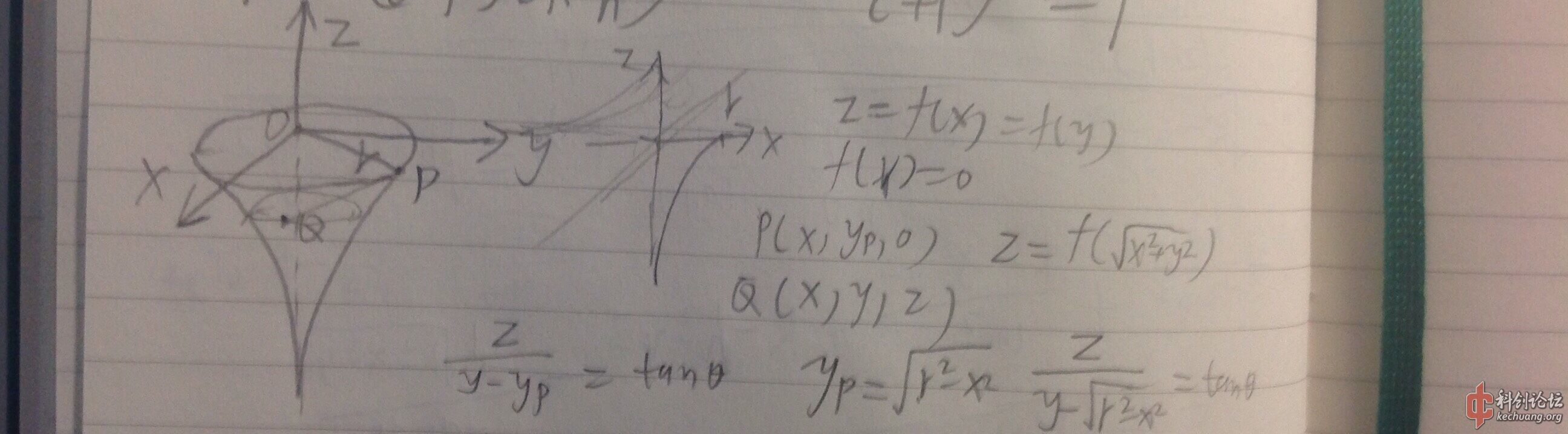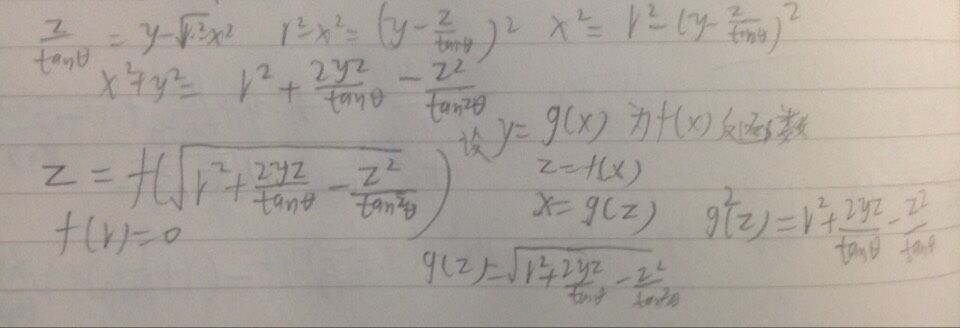家里有一个死星的模型，有一天看到凹形碟处的影子形状很像个圆，到底是不是呢？我先证了圆的，然后到一般情况，发现这样一个结论：对于某些形状的曲线形成的旋转体，向垂直轴心的截口（圆的）射去平行光，在旋转体上成的影子边界形状在一个平面内，也就是一个平面截这个旋转体。这个平面是很好确定的。
  这是死星（死星地球仪）
这是证明。其实证明并不难，主要是结论比较有趣

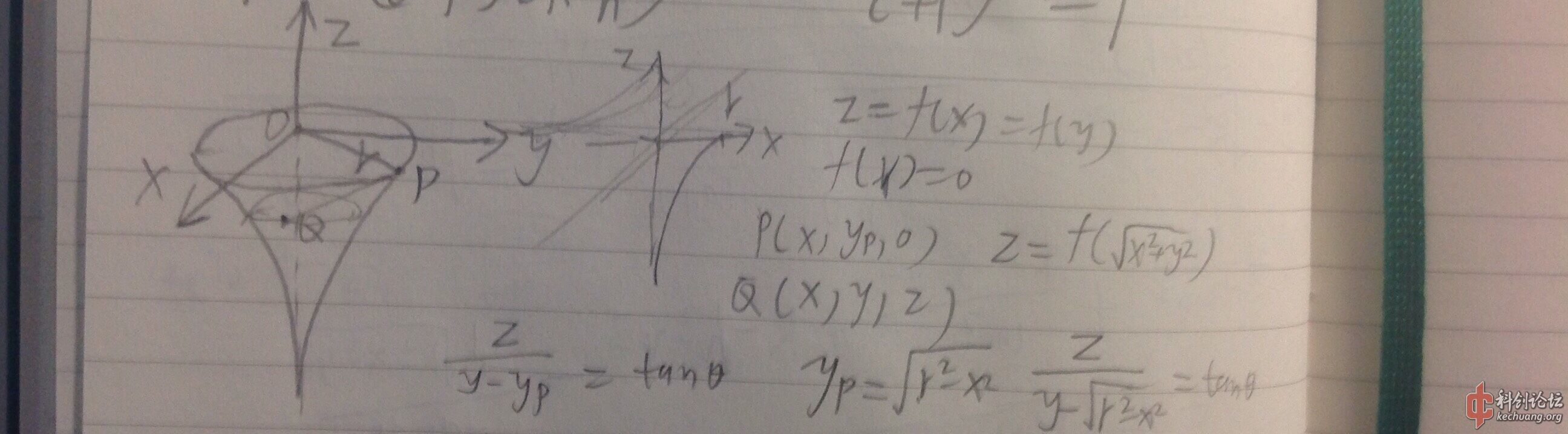
要证在一个平面内只要证YOZ平面内点的轨迹共线。不小心用了左手系，问题不大。

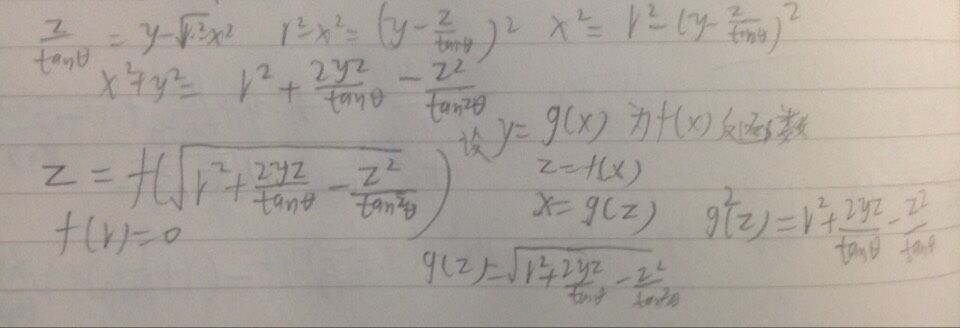
所以截面函数f(x)的反函数g(x)=r^2+Az^2+Bz
据我考虑到的情况，f(x)可以是：.各种直线 ，中心在z轴上的圆、椭圆、双曲线、抛物线（的一部分）。
所以可以成类似以下的旋转体

也就是说光从这些壳的口里射进去，成的影子边界形状在一个平面上。所以假如死星的聚焦碟是球冠的壳，所成的影子形状就是个圆，据计算（不是普遍的）圆的半径和球冠边界的半径相等。但假如侧面曲线不是这些类型的，影子应该就不在一个平面内。
    这个有什么用呢？比如说画素描要画一个碗，要画影子，就可以大胆地按圆画吧。