方法一:定积分
方法二:按不同颜色区域的面积设未知数,建立方程组
@drzzm32 @radio 这些方法都很复杂。我自己都搞不定~ 积分是个很强大的方式。可惜是高数的范围。 用弓形加三角形。计算难度也很高。
不知道小学生学过概率了没。我记得简单的概率运算是在高中最后才学的。现在的小学生学的东西感觉比以前的深奥一些。
我的解法思路是,把面积交集的问题转化成概率问题。这样只需要做分数运算就可以得出答案。运算步数非常少。这个方法是小学生最可能的方法。
只需要算出正方形当中的点,出现在红色区域的概率。这个问题很好解。
正方形面积设为S1;大扇形面积设为S2和S2’ ;最小的扇形设为S3 ;设红色区域面积为Sr。
S1=a²
S2=S2‘=πa²/4
S3=πa²/8
点出现在大扇形的范围内的概率P2等于S2/S1,以此类推
P2=P2‘=π/4
P3=π/8
接下来正方形内所有的点出现在红色区域的概率设为Pr。
Pr=P2*P2*P3=π/128 (这步算错了,应该为π³/128)
所以
红色区域Sr=πa²/128(之前算错,更正为:π³a²/128)
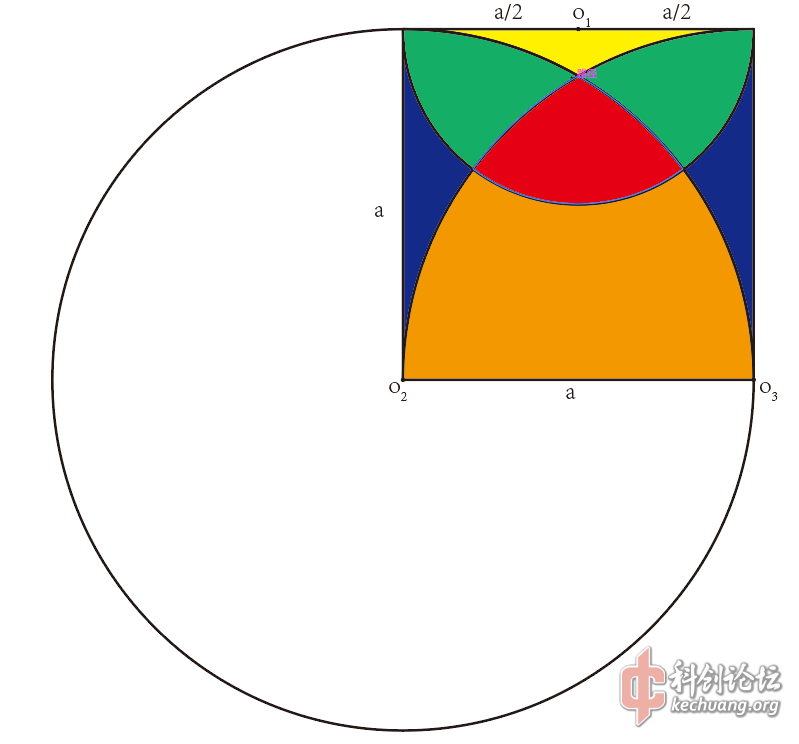
可是~红色区域怎么看也不像是只是大圆的1/128的样子~~
哎·~
手生了,不知道有没错。
(3*arcsin(0.8)/4 - sqrt(3)/4 - π/24)*a²
大约0.13156*a²

之前分数乘法搞错了...........
丢了好多年的数学...
(π/4)*(π/4)*(π/8)=π³/128
....................
所以 红色的面积实际上是 a²π³/128
0.24223653656484234512090871146173*a²
面积约等于正方形面积的24.2%
楼主可以用概率的方法算一下这两个图形红色部分的面积,看它们的结果是否一样。

这个问题考点应该是两个圆重叠区域的面积,两个圆的扇形,减去辅助三角形。中学生列方程直接一些,但是小学不能用,小朋友可以用替换法。要细心代数,非常容易算错。。。结果好像近似等于0.13156*a²。。。
把红色三个顶点连接,切出一个三角形,通过测量算出三角形面积;
然后把剩下三个弧分别做一个圆(椭圆?),测量弧长,算出面积(或者建立坐标系二次函数法搞出面积)
最后相加
题目没说不能测量
(考试有的题做不出来我们就这么搞,俗称“科学测量法”)
@drzzm32 @radio 这些方法都很复杂。我自己都搞不定~ 积分是个很强大的方式。可惜是高数...
这个方法不对。
这个算法完全没有考虑各个形状的位置,也就是说不论扇形位置如何求出的重叠面积都是一样的。然而移动其中图形的位置明显会产生面积变化,例如把最上面那个半圆形翻转到底下那边来,面积明显与原来不同。
| 时段 | 个数 |
|---|---|
| {{f.startingTime}}点 - {{f.endTime}}点 | {{f.fileCount}} |
200字以内,仅用于支线交流,主线讨论请采用回复功能。