这个轨道本身是有直径的。。用电感梯度算会把导轨内部径向电流的受力也算进去。。当弹丸的宽度为无穷小时,这样求出的受力就全部是导轨内部径向电流的受力了。。
加载中
加载中
表情图片
评为精选
鼓励
加载中...
文件下载
加载中...
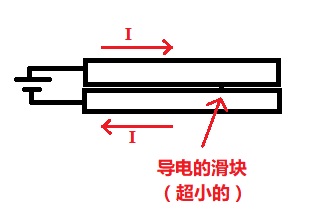
没看过电炮类的书籍。。。不过试着推了下,看看对不对
考虑两个平行细长导线组成的导轨,内部通相反方向电流,距离为d,长度为l,然后l>>d
则中间位置距离其中一个导线距离为r处产生的磁场为
而这个结论要成立需要满足上面提到的前提
长度l相对于宽度d足够长
导轨半径w相对于宽度d足够小
主贴的情况无法满足第二个前提
200字以内,仅用于支线交流,主线讨论请采用回复功能。