PS:提到进展,意思就是还没全搞出来……(不过应该快了)本贴不涉及“已经搞出来的部分”的求解过程。等搞定全部内容后,会把相关结果连过程一起发出来的。
首先定义一下本贴里的“最优”。本贴提到的最优,是指“在使用某一种导体作线圈,某一种磁材料作弹丸时,在给定管壁厚度下,给定距离内,把弹丸加速到目标速度时,线圈电阻损耗的电能最小”。这个“最优”是理论上的最优,同所有理论最优一样,它工程上不可实现,因为它要求线圈充满炮管外无穷大空间,然后还可以完全自由的操纵线圈中的任意一点的电流密度……但是可以逼近,比如线圈长度小于内径,各级紧密相靠,然后细线绕内层,粗线绕外层……注意根据定义,这个最优里,其实已经没有线圈这种东西存在了,因为线圈的概念被“电流密度分布”代替了……
(关于这个最优,想象右边灰色的弹丸沿着白色的炮管,在黄色代表的电流密度分布产生的磁场作用下,被一直加速到左边飞出去)
![猜想的电流密度分布.jpg]()
有了目标就可以开始分析了。磁阻式电磁炮想要精确分析的话,最大的难点就是铁磁材料的非线性磁化。不过,在磁饱和条件下,非线性的磁化会变成恒定不变的磁化,反而变成了最容易分析的情况。
记得很久之前我提到过,在这个条件下磁阻式电磁炮的理论最优解,可以简化分解为如下两个问题:
1.
[求教]一个假的运动学问题2.
送大家一个课题:线圈炮的最佳电流密度分布第一个问题是,如何分配加速段上各点加速力的大小,才能在给定出速下,电阻损耗能量最小。
第二个问题是,如何分配各点的电流密度,才能在产生给定加速力的情况下,电阻损耗功率最小。
把这两个问题的结果加起来,就是在把弹丸在给定距离内,加速到给定速度时,线圈电阻损耗的电能最小的加速方式。也就是顶上提到的最优。这两个问题能加起来的前提条件是,电磁力和弹丸的速度以及绝对位置无关,只和空间中的电流密度分布情况与弹丸的相对位置有关。
目前的情况是,第一个问题已经被解决了,结果就是位移的三阶导数等于0,或者说,使用恒定加速力效率最高。这个是解析解。
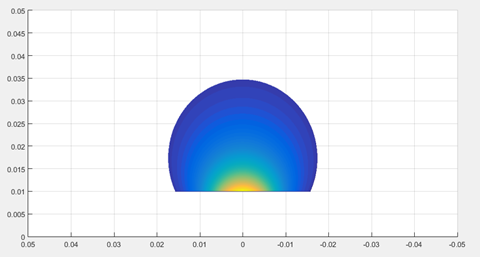
第二个问题目前搞出来了这么个东西:
![image.png]()
简单的说就是,用固定直径导线绕的线圈,截面长这样的时候,在它中心点产生磁场的能力最强。
复杂的说就是,线圈各点电流密度大小相同的条件下,截面形状长这样的线圈,在线圈中心产生给定磁感应强度的时候,电阻损耗的功率最小。
图中,带颜色的地方是有线圈的地方,线圈上的颜色没有实际意义,横轴为线圈的对称轴,因为线圈截面的上下两部分关于横轴对称,所以仅画出其中一半。可以绕线的空间被限制在纵轴的0.01以上,两个坐标轴上的数值仅具有比例上的意义。这个理论上讲可以是纯解析解,不过形式上会无比麻烦,所以实际上是半解析半数字搞的。
目前仍需要搞的是第二个问题,要把“电流密度大小相同”这个限制条件去掉,还要把“在线圈中心产生给定磁感应强度”这个条件改成“在弹丸上产生给定电磁力”
感觉等这个最优解搞出来了后,再分析一个磁阻式电磁炮的时候,就可以根据它的参数,算出其理论最优解对应的效率,然后用实际效率除以理论效率,求出来一个“归一化效率”。当对两个磁阻式进行比较的时候,用这个归一化效率的话,应该就可以很大程度上减小比如口径这种参数对效果的影响,更有效的判断出比如驱动方式,线圈工艺等方面的优劣了……
 。感觉在匀加速的工程方案模型中,再进一步探讨电流密度的影响会更有指导意义一些
。感觉在匀加速的工程方案模型中,再进一步探讨电流密度的影响会更有指导意义一些 。
。 。
。 。感觉在匀加速的工程方案模型中,再进一步探讨电流密度的影响会更有指导意义一些
。感觉在匀加速的工程方案模型中,再进一步探讨电流密度的影响会更有指导意义一些 。
。 。
。
200字以内,仅用于支线交流,主线讨论请采用回复功能。