限制波尔次曼机(RBM)
中文论文见层尾
限制波尔次曼机是一种无监督单层神经网络。
无监督和监督的区别在于无监督不需要在训练的时候提供输出层数据，因为无监督神经网络可以“自主学习”：即可以自行抽取出输入数据的特征，对不同的输入数据进行分类（输出不同的结果），同时也具有较良好的泛化能力（指对新鲜样本的适应能力）。
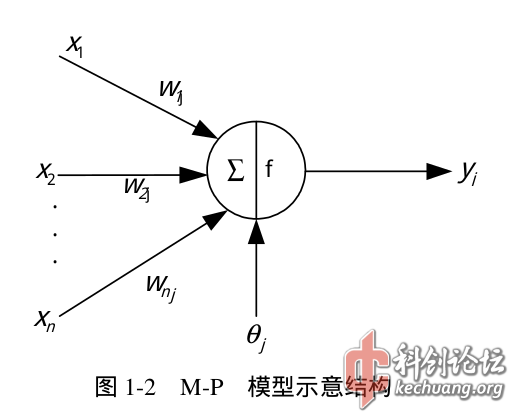
如图，RBM有n个可见单元和m个隐单元，用向量V和H表示，W是RBM的连接权值矩阵，向量A、B分别表示可见单元、隐单元的偏置（oh，前面忘记讲了，就是M-P模型中的theta，用来修正神经元的输出）。
![blob.png]()
在RBM里，大家可能对能量状态和激活概率感到陌生。
能量函数参考文献[1]，这里做简单说明：能量函数代表神经网络的稳定程度，值越小代表神经网络越稳定，分类性能最好，在监督学习中，能量函数通常与输出层数据与期望值之间的误差有关，而在RBM中则与两个层的数据分布概率有关:
$$E(v,h|\theta)=-\ln P(v,h|\theta) + const$$
注：\(\theta\)是指神经网络的配置，包括W、A和B。
而整个神经网络的值函数是各个数据的值函数的累加。
$$E(\theta)=\sum_{v,h}E(v,h|\theta)$$
由此可见，数据分布越平均，值函数越小，而整个神经网络就越稳定。
RBM的数据分布概率定义为：
$$E(v,h|\theta)=\sum_{i, j} W_{ij} v_{i} h_{j} + \sum_{i} a_{i} v_{i} + \sum_{j} b_{j} h_{j}$$
以此为基础，我们可以计算出它的联合概率分布：
![blob.png]()
在这里值得大家注意的是，我们所关注的数据分布概率是可见层v的分布\(P (v|θ)
\)，即即联合概率分布\(P (v,h|θ)\) 的边际分布。
![blob.png]()
激活概率可以理解为神经元的的输出，因为：
![blob.png]()
![blob.png]()
眼熟？没错，这就是神经元的输出，只不过在可见层和隐层的计算中，权值是对称的。
这里RBM使用一种基于对比散度的训练方法,各参数的更新准则为:
$$ \Delta W_{ij}=\eta (<v_i h_j>_{data} - <v_i h_j> _{recon} ) $$
$$ \Delta a_{i}=\eta (< v_i > _{ data } - < v_i > _{ recon } ) $$
$$ \Delta b_{j}=\eta (< h_j > _{ data } - < h_j > _{ recon } ) $$
\(<·> _{ data } \)表示初始的数据分布， \(<·> _{ recon } \)表示一次重构后模型的数据分布。
简单来说，我们输入\(v1\)得到\(h1\),从而用\(v2\)和\(h2\)计算出分布 \(<·> _{ data } \)，但还没结束，我们要用对称的权值从\(h1\)计算出\(v2\)（重构后的可见层），计算出\(h2\)（重构后的隐层），然后用\(v2\)和\(h2\)计算出的分布是\(<·> _{ recon } \)。
详细的公式：
![blob.png]()
下面贴论文和代码。
RBM.h:
<code class="language-c">#include <stdlib.h>
#include <math.h>
namespace MWS{
//**********************************
//函数描述:返回符合正态分布的随机值
//**********************************
double R(){
return sqrt(-2*log(rand()/(RAND_MAX+1.0)))*cos(2*3.14159265*rand()/(RAND_MAX+1.0));
}
//**********************************
//函数描述:返回从0到1的随机值
//**********************************
double r(){
return rand()/(RAND_MAX+1.0);
}
//**********************************
//函数描述:S型函数
//**********************************
double sigmoid(double x)
{
return (1.0/(1.0+exp(x)));
}
//****************************************************
//类:受限波尔兹曼机
//作者:黄涛
//日期:2016年7月29日
//描述:受限波尔兹曼机是一类具有两层结构、对称连接且无
//自反馈的随机神经网络模型,层间全连接,层内无连接。
//备注:深度信念网络测试用
//****************************************************
class RBM{
public:
double eta;
//eta:学习率
double *v,*h;
//v:可见层(n)
//h:隐层 (m)
double **W,*a,*b;
//W:权值(n*m)
//a:可见层偏置(n)
//b:隐层偏置(m)
int m,n;
//m:隐层单元个数
//n:可见层单元个数
//**************************
//函数描述:类初始化
//**************************
RBM(
int m_in,
//m_in:隐层单元个数输入
int n_in,
//n_in:可见层单元个数输入
double eta_in=0.95
//eta_in:学习率输入
){
eta=eta_in;
m=m_in;
n=n_in;
v=new double[n];
h=new double[m];
W=new double*[n];
a=new double[n];
b=new double[m];
for(int i=0;i<n;i++){ a[i]="R();" w[i]="new" double[m]; for(int j="0;j<m;j++)" { w[i][j]="R();" } i="0;i<m;i++){" b[i]="R();" w,a,b初始化时均为符合正态分布的随机值 ************************** 函数描述:训练 void tran( double *x0, x0:训练样本(n) int t t:最大训练周期 ){ *v1="x0;" h1[m]; v2[n]; p_h1[m]; p_v2[n]; p_h2[m]; 计算概率 e="0;" e+="v1[i]*W[i][j];" p_h1[j]="sigmoid(b[j]+E);" if (r()<="P_h1[j]){" h1[j]="1;" }else{ p_v2[i]="sigmoid(a[i]+E);" v2[i]="1;" p_h2[j]="sigmoid(b[j]+E);" 更新权值 w w[i][j]+="eta*(P_h1[j]*v1[i]-P_h2[j]*v2[i]);" a a[i]+="eta*(v1[i]-v2[i]);" b b[j]+="eta*(P_h1[j]-P_h2[j]);" 函数描述:计算 calculate( *x x:输入(n) h[j]="sigmoid(b[j]+E);" }; < code></n;i++){></math.h></stdlib.h></code>
RBM.cpp:
<code class="language-c">#include <stdio.h>
#include <time.h>
#include "RBM.h"
MWS::RBM test(4,10);
double x0[10][10]=
{
{1,2,3,4,5,6,7,8,9,0},
{2,3,4,5,6,7,8,9,0,1},
{3,4,5,6,7,8,9,0,1,2},
{4,5,6,7,8,9,0,1,2,3},
{5,6,7,8,9,0,1,2,3,4},
{6,7,8,9,0,1,2,3,4,5},
{7,8,9,0,1,2,3,4,5,6},
{8,9,0,1,2,3,4,5,6,7},
{9,0,1,2,3,4,5,6,7,8},
{0,1,2,3,4,5,6,7,8,9}
};
double result[10][4];
int main(){
srand(time(NULL));
for (int i=0;i<100;i++){ for (int j="0;j<10;j++){" test.tran(x0[j],10); } i="0;i<10;i++){" test.calculate(x0[i]); result[i][j]="test.h[j];" printf("%f,",result[i][j]); printf("\n"); return 0; < code></100;i++){></time.h></stdio.h></code>
这个cpp没有太大意义，只是测试RBM的特征抽取能力，下图是结果（不同的颜色代表不同的维度，序号表示输入样本编号，高度代表输出值的大小）
![blob.png]()
输出的.csv结果下载：
RBM.csv
0.89KB
CSV
44次下载
E文论文：
Training Products of Experts by Minimizing.pdf
1003.53KB
PDF
42次下载
预览
神奇的文件大小显示:-(
参考文献：
- [1]:章毅, 王平安. 关于神经网络的能量函数[J]. 计算机研究与发展, 1999, 36(07):794-799.
- 下载：
受限波尔兹曼机简介.pdf
1.09MB
PDF
366次下载
预览
200字以内，仅用于支线交流，主线讨论请采用回复功能。