一、磁阻炮用线圈参数选型表
部分截图:
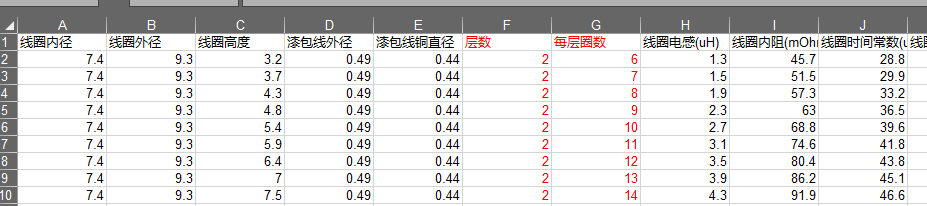
表格中包含:线圈外形尺寸信息、漆包线信息、绕制层数&每层圈数、线圈电感、线圈内阻、时间常数等
使用方法:表格按线圈内径分为25页(每页约一万行),找到你所需要内径所对应的那一页,搜索需要匹配的参数。
Excel中搜索方法:暂略
此处表格扫描参数如下:
线圈内径范围4.8-9.8mm,0.2mm步进;
漆包线外径范围0.49-1.2mm,共25种;
线圈层数范围2-16层;
每层圈数范围6-40圈;
形状过长/过扁的线圈不计入
以上参数范围依照经验选取,受文件大小等因素限制,暂未上传覆盖更广的表格。如果您想寻找的线圈不在表格中,请往下翻。
二、一种靠谱的多层空心线圈电感计算方法
单层螺线管型空心线圈、单层蚊香型空心线圈的电感计算公式很常见且结果精确,但多层螺线管型线圈(典型的磁阻炮线圈)的电感计算公式比较少见。多层线圈之间互相磁耦合,其电感计算较为复杂(不能把多个单层线圈电感量累加)。网络资料中可见一些近似计算公式,但经验证,应用于磁阻炮线圈电感计算时,其计算结果误差较大。
文献[1]中给出了一种多层空心线圈电感的计算方法,文献使用图表来确定电感形状系数Φ,其计算过程如下:
\[L = \frac{{{u_0}}}{{4\pi }}{N^2}{d_0}\Phi \]
代入真空磁导率u0 ,并调整单位数量级后:
\[L = {N^2}{d_0}\Phi \cdot {10^{\rm{4}}} \] 其中: L -电感量(uH)
N -线圈总匝数
d0 -线圈平均直径(mm), \({d_0} = \frac{{{d_1} + {d_2}}}{2}\)
Φ -电感形状系数(常数),见下图


其中,α 、ρ 是与线圈外形相关的常数

\[\rho = \frac{\delta }{{{d_0}}}\]
\[\alpha = \frac{h}{{{d_0}}}\]
关于系数曲线图的高清无码版与更形象的计算说明,请查阅文献[2]。
作者验证了数个磁阻炮线圈,计算结果与实测结果接近,误差小于10%。
此方法得到的是近似数值,期待坛友指出解析解的计算方法。
三、计算程序的实现
计算程序使用Python 3.6.2编写,主要分为三个模块:扫描参数生成器、电感计算模块、内阻计算模块
使用库:math、numpy、scipy
电感计算模块中,参照文献[1]原图表,人工描点取得了75组参数。
下列数值中Z[i]=f(u[i],v[i]) 即为电感形状系数函数Φ=f(α,ρ) 的样值点
Z =([1.8,1.8,1.8,1.8,2,2,2,2,2,2,2.5,2.5,2.5,2.5,2.5,2.5,3,3,3,3,3,3,3,3,3.5,3.5, 3.5,3.5,3.5,3.5,4,4,4,4,4,4,4.4,4.4,4.4,4.4,4.4,4.4,5,5,5,5,5,5,6,6,6,6,6,6,7,7,7, 7,7,7,8,8,8,8,8,8,10,10,10,10,15,15,15,20,20]) u =([0.8,0.6,0.4,0.2,1,0.8,0.6,0.4,0.2,0,1,0.8,0.6,0.4,0.2,0,0.92,0.7,0.5,0.2,0.1, 1,0.9,0.8,1,0.8,0.6,0.4,0.2,0,1,0.8,0.6,0.4,0.2,0,1,0.8,0.6,0.4,0.2,0,1,0.8,0.6,0.4, 0.2,0,1,0.8,0.6,0.4,0.2,0,1,0.8,0.6,0.4,0.2,0,0.8,0.6,0.4,0.2,0.1,0,0.5,0.3,0.1,0,0.2,0.1,0,0.1,0]) v = ([3.02,3.32,3.73,4.32,2.48,2.64,2.92,3.3,3.84,4.52,1.8,1.96,2.2,2.52,2.96,3.52, 1.4,1.6,1.86,2.4,2.6,1.36,1.45,1.5,1.05,1.16,1.36,1.64,1.96,2.36,0.78,0.9,1.1,1.35, 1.64,2,0.62,0.74,0.93,1.17,1.46,1.8,0.42,0.55,0.72,0.94,1.2,1.5,0.15,0.3,0.46,0.67, 0.9,1.2,0,0.12,0.28,0.48,0.7,0.95,0,0.14,0.32,0.54,0.68,0.78,0.03,0.2,0.42,0.53,0.2,0.12,0.22,0,0.1])
取得样值点后,通过Python Scipy库中griddata()函数对样值点进行三次样条插值(对类似的平滑曲面,cubic插值法有着较好的效果)。
points = np.vstack((u,v)).T #两个坐标数据数组合成为二维坐标点 x1=np.arange(0,1,0.01) y1=np.arange(0,3,0.01) x, y = np.meshgrid(x1, y1) Inductor_Coeff=np.array(scipy.interpolate.griddata(points,Z,(x,y),method ='cubic')) #Out为系数输出矩阵,二维
至此完成图表的数字化重建,得到的二维数组Inductor_Coeff为Φ=f(α,ρ)的高密度插值数组,网格密度0.01,数组在α方向范围0-299;在ρ方向范围0-99。
将计算好的α、ρ值放大一百倍,四舍五入取整后作为坐标,从二维数组Inductor_Coeff中寻找对应的Φ值即可。
内阻计算模块中,分别计算出每层漆包线绕成螺线管的平均直径,再求得每层漆包线所用漆包线长度,累加得整个线圈所用漆包线长度。再根据引线长度、导体截面积、电阻率等信息,易得线圈内阻。
参数扫描模块中,生成的线圈参数可能会使得α、ρ值超出数组索引范围,故进行范围检测,如果溢出,那么这组线圈参数将不被计入表格。
计算器V1.1手动输入版exe下载:
计算器V1.1手动输入版源码下载:(Python3.6.2)
与批处理版本相比,存入了完整的插值数组(为了省略插值运算库,缩小体积),数组索引顺序略有变动。
四、如果表中没有您需要的参数范围,请参照此处修改程序
自动生成器脚本代码在此下载:(非程序猿,文风不好请见谅,不负责解决脚本运行问题
测试Python版本为3.6.2
如需修改参数扫描范围,请修改主函数中以下内容:
(请注意当生成的线圈参数总行数超过某数值时会导致某模块内存溢出,请注意总行数数量,笔者实测500000行可运行。
#使用线径 [漆包线外径;漆包线铜直径](mm) Line_D=(np.array([[0.49,0.44],[0.52,0.47],[0.54,0.49],[0.56,0.51],[0.58,0.53], [0.6,0.55], [0.62,0.57],[0.64,0.59],[0.67,0.62],[0.69,0.64], [0.72,0.67],[0.74,0.69],[0.78,0.72],[0.8,0.74], [0.83,0.77], [0.86,0.8], [0.89,0.83],[0.92,0.86],[0.96,0.9], [0.99,0.93], [1.02,0.96],[1.07,1.0], [1.12,1.04],[1.16,1.08],[1.2 ,1.12]]))
此处数组表示参与参数扫描的漆包线参数,如需扩充请自行添加,程序能够自适应二维数组长度。
Coil_Din=np.arange(4.8,9.8,0.2) #线圈内径,4.8-9mm,0.2mm步进 Coil_Layer=range(2,16) #线圈层数,2-16层 Coil_CirNum=range(6,40) #每层圈数,6-40圈 Coil_D_Max=16 #线圈最大单边厚度16mm Coil_H_Max=41 #线圈长度最大41mm
Coil_Din表示线圈内径范围,(最小内直径,最大内直径,步进)
Coil_Layer表示线圈层数范围,(最小层数,最大层数),步进为1
Coil_CirNum表示每层圈数,(最小圈数,最大圈数),步进为1
Coil_D_Max表示线圈最大厚度(线圈外半径-线圈内半径)
Coil_H_Max表示线圈最大长度(高度)
五、反馈方法:向我发送站内信,较多数据(>5组)建议回帖
本人不保证该计算方法、计算程序及选型表的准确性,但期待您提供更多数据来修正计算器。修正反馈格式如下:
(长度单位如无特别说明,均为mm)
常用参数[线圈内径;漆包线外径;铜直径;层数;每层匝数;总引线长度]
(可选)不常用参数[匝间缝隙;电阻率(欧姆每平方毫米每米,20摄氏度);电阻温度系数;温度(摄氏度);导体材料密度(g/cm^3)]
计算输出参数[线圈内径;线圈外径;线圈高度;线圈电感(uH);线圈内阻(毫欧);线圈时间常数(us);线圈铜质量(g);线圈线长(m)]
实际参数[参数类型与单位如上]
备注:线圈工艺(手绕/工具绕制/机械自动绕制);仪器信息
不想填的项目请用*号占位
示例:常用参数[7.1,0.64,0.59,4,24,100]
不常用参数[0.05,*,*,20,8.9]
计算输出参数[7.1,12.0,16.5,32.4,182.8,177.3,7.2,3.11]
实际参数[7.1,12.3,16.2,32.2,203,*,*,*]
备注:手工绕制;5%精度数字电桥&1KHz
结语:
由电感计算公式可以看出,当线圈的外形确定时,选用不同的漆包线线径可以获得不同的时间常数。
依照得到的线圈选型表,在约束条件下搜索(如:线圈内径7.2mm,线圈外径12+-1.5mm,线圈长度16+-1mm,时间常数150+-30us),那么可得到对应的线圈绕法。
换言之,可以依据电路的集总参数要求、机械尺寸约束,得到绕线方法。
参考文献:
[1] 陈汤铭. 电感计算手册 [M]. 北京: 机械工业出版社,1986:263-267.
[2] 潘永生,陶乐,刘虎.你好,电磁炮[M].北京:科学出版社,2019: 109-110.
[修改于 4年9个月前 - 2020/02/28 13:54:06]