想了关于拦截物体怎么实现的一个问题，后面解的很简单，只是分享出来，希望能够启发各位

看了很多自制小玩意儿的帖子，能不能搞一个自动识别来袭物体，并自动拦截的系统。

（或者拦截什么最近流行的高楼坠物，或者自我防御系统，拦截巡航无人机）

以拦截恒定加速度物体（如自由落体、◎形推力的）为问题思考：

在此之间，大家可以先自己先思考10s，自己该怎么做，如何测量？如何计算？考虑v，a的变化？拟合速度v？

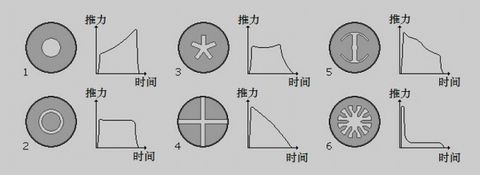
假设前提：

1、这主要针对非矢量推进物体。即在发现-摧毁时间内，不会突然改变。

2、己方拦截物体也是拥有自平衡直线发射能力，加速度，方向不变。（即环形推进孔，如上图）

3、双方物体，除了自平衡飞控，无其他针对拦截做出策略的算法。

4、己方拦截物体，具有计时末端、范围性张开（如网状）。（主要是避免撞不上，消除这个误差。通过爆炸间接摧毁）

5、主要针对拦截，飞行中段、末段等，加速度平稳的时期。

Step1：敌方物体拟合

测量，应该用雷达，得到数据，这里直接采用得到三维的x、y、z数值，具体换算就不深层考虑，不懂雷达，换算应该不难。

假设监测1~10s，每秒一个数据。（实际越快得到越多数据，越利于拟合的准确性。）

    1  2  3  4  5  6  7  8  9  10

x

y

z

之前我想着混合x,y,z三数值，一起拟合为一个大函数。并且己方导弹也是一个三参数的拟合函数。两个联立求解。

在纸上算了下，发现把问题想复杂了。很简单，直接x，y，z轴，三轴单独拟合计算就可以了。

和速度，分速度分解是一样的，书读多了，想的复杂了

上面数值，x轴，单独拟合与时间的函数。（y、z轴同理）

t秒到达x_t点，假设a为定值，则路径l与时间t函数是二次t2的多项式。（用mathlab的二次多项式拟合即可）

这样就 t 秒，到达（x_t，y_t，z_t）点。

Step2：己方物体计算

这个就简单了。

也是三个轴分别算，假设加速度a固定。

1/2*a_xt²，给出三轴的分加速度即可。

a_x=a*sin(α)*sin(β)

x、y、z三轴，t秒时，三个坐标值相等。建立三个方程组

包含α、β、t，三个未知数，联立求解。

确定发射角度、以及开网延时时间（爆炸范围）。发射后，耗尽延时时间，自动爆炸，范围伤害拦截敌弹，减少误差。

后续改进方向：

1、己方发射物自身误差。在z轴，需要去掉自身重力，即去掉1个g。

2、◎形填药，前段的小段推力增加过程，可以修正这部分误差。

3、针对其他几种填药方式。其实都是针对加速度a可以，2次曲线的一个二次多项式拟合。

加上原来a为定制的路径公式，l=at²，只需要再加上2次，利用t⁴拟合，这个四次多项式，拟合结果应该更精确。

4、只需要一个旋转xy轴、一个俯仰z轴的装盘组合。由于旋转到固定发射角需要一定时间，后续可以修正这个延时误差

突然想到这个点子，计算确实太简单，写得仓猝，重在启发大家，有没有什么好的想法？

或者整合雷达、单片机、土豆炮，关键在于自动拦截，发现-识别-计算-拦截。

如果开发高楼坠物系统：

感觉需要速度检测器，一旦超过额定值，激发系统。

用网状物发射，兜住尖刀。

或者激发一楼，弹出什么雨棚之类的挡住。