这个轨道本身是有直径的。。用电感梯度算会把导轨内部径向电流的受力也算进去。。当弹丸的宽度为无穷小时,这样求出的受力就全部是导轨内部径向电流的受力了。。
82281
%7B%22isLastPage%22%3Atrue%2C%22notes%22%3A%5B%5D%2C%22pid%22%3A%22839038%22%2C%22tid%22%3A%2282281%22%2C%22mainForumsId%22%3A%5B%22367%22%5D%2C%22categoriesId%22%3A%5B%22241%22%5D%2C%22tcId%22%3A%5B%5D%7D
%7B%22isEditMode%22%3Afalse%7D
求教:轨道炮的电磁力,和“电感梯度”是啥关系?以及“电感梯度”到底是啥?
标题里的问题,其实是由下面这个问题引出来的。
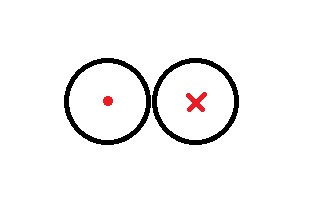
假设有两根等径圆形导线紧贴在一起平行放置,如下图(轴向图)。
![紧贴的双轨(轴向).jpg]()
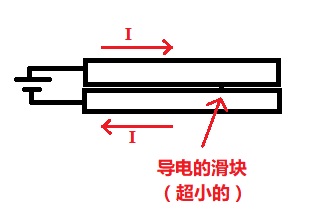
两根导线之间有一个极窄的间隙保证绝缘,同时在足够远处被一个(极小的)导电的滑块连在了一起。然后我们给这两根导线通一个电流,如下图(俯视图)。
![紧贴的双轨(俯视).jpg]()
下面来考虑一下,那个导电的滑块会不会受力。
第一个思路是,根据F=BIL,由于两根导线间的间隙极窄,即L趋近于零,而B和I都是有限值,所以那个滑块不会受力。
然而还有另外一种思路。根据电感的定义可以算出,这两根导线组成的导体系统,从电源看过去,单位长度的电感量为0.1uH,或者说,电感梯度是0.1uH/m(貌似是……最近电磁场复习的有点晕,不知道对不对……不过反正它单位长度的电感不会是0),那么根据F=0.5*I^2*dL/dx,那个滑块就会受一个不是太小的力。
所以……上面两种思路得到的结论不同,问题出在哪?
由此引出:轨道炮的电磁力和电感梯度,到底是啥关系?通常所说的那个电感梯度,和单位长度的电感又是啥关系?
假设有两根等径圆形导线紧贴在一起平行放置,如下图(轴向图)。
两根导线之间有一个极窄的间隙保证绝缘,同时在足够远处被一个(极小的)导电的滑块连在了一起。然后我们给这两根导线通一个电流,如下图(俯视图)。
下面来考虑一下,那个导电的滑块会不会受力。
第一个思路是,根据F=BIL,由于两根导线间的间隙极窄,即L趋近于零,而B和I都是有限值,所以那个滑块不会受力。
然而还有另外一种思路。根据电感的定义可以算出,这两根导线组成的导体系统,从电源看过去,单位长度的电感量为0.1uH,或者说,电感梯度是0.1uH/m(貌似是……最近电磁场复习的有点晕,不知道对不对……不过反正它单位长度的电感不会是0),那么根据F=0.5*I^2*dL/dx,那个滑块就会受一个不是太小的力。
所以……上面两种思路得到的结论不同,问题出在哪?
由此引出:轨道炮的电磁力和电感梯度,到底是啥关系?通常所说的那个电感梯度,和单位长度的电感又是啥关系?
没看过电炮类的书籍。。。不过试着推了下,看看对不对
考虑两个平行细长导线组成的导轨,内部通相反方向电流,距离为d,长度为l,然后l>>d 则中间位置距离其中一个导线距离为r处产生的磁场为 $$B=\frac{\mu_0I}{2\pi r}+\frac{\mu_0I}{2\pi (d-r)}$$ 为了避免积分出现问题,忽略导线半径\(w\rightarrow0\)内的磁场 即在0+w到d-w内对磁场积分,乘以长度l得到磁通: $$\phi=\frac{l\mu_0 I}{\pi} ln(\frac{d}{w})$$ 自感电动势 $$E=\frac{l\mu_0\partial I}{\pi\partial t} ln(\frac{d}{w})$$ 自感 $$L=\frac{l\mu_0}{\pi}ln(\frac{d}{w})$$ "电感梯度“ $$\frac{L}{l}=\frac{\mu_0}{\pi}ln(\frac{d}{w})$$ 对于导轨两端的磁场,是只有半边的无限长直导线 $$B_端=\frac{\mu_0I}{4\pi r}+\frac{\mu_0I}{4\pi (d-r)}$$ 弹丸受力 $$F= I\int^{d-w}_wB_端dr$$ 即 $$F=\frac{I^2\mu_0}{2\pi}ln(\frac{d}{w})$$ ”电感梯度"和弹丸受力正好有 $$F=\frac{1}{2}I^2\frac{L}{l}$$ 的关系
而这个结论要成立需要满足上面提到的前提
-
长度l相对于宽度d足够长
-
导轨半径w相对于宽度d足够小
主贴的情况无法满足第二个前提
引用
2
加载评论中,请稍候...
200字以内,仅用于支线交流,主线讨论请采用回复功能。