上次不会加图片，所以好像在茶话都被删了…庆祝终于能发帖了，所以再发一遍~这是我和我朋友做的火箭，今天发鸭翼的分离时的PID部分，数据和实际测试出入不小，还在修改完善中，请勿见怪~因为涉及到分离和寻地，所以有参数很夸张，因为在分离的时候速度降的很厉害~我们做火箭只是出于个人爱好，水平及其业余，实验室给的钱基本，哈哈…甚至获奖的钱还得交回去，再哈哈…反正进度缓慢，知识匮乏，没人帮，测试也不靠谱，发这么一个不成熟的东西上来只是希望唤起大家对运动控制的爱，让KC的火箭发展多元化~还有就是互相多多交流~
献丑了~
鸭翼控制。根据导弹的受力分析、力矩平衡入手列写微分方程,若仅考虑弹体的姿态变化,且忽略速度变化的影响和一些次要因素,如重力影响、下洗延迟等,采用小扰动法理论,则可得到导弹纵向短周期运动简化方程组

其中K1表示单位舵角作用下能产生的弹道倾角速度;T1表示弹道倾角相对导弹姿态角所具有的惯性;T表示导弹攻角跟踪舵偏角的快慢程度;ξ是导弹的阻尼系数。
采用将修正因子模糊数模型在线插值的方法对导弹姿态进行控制。经典的模糊控制器是一个相当于PD控制器，稳定性不能达到要求，所以在其中加入积分环节，以提升控制器的稳态性能。并采用有修正因子的模糊数模型,并对其进行在线插值,能使所设计的模糊控制系统具有在线自调整控制规则的功能。
采用如下控制规则

为在线自调整修正因子。选取适当的模糊模型，则可以得到控制器的控制规则。此规则的任务主要是在线自调整修正因子α,对修正因子α的模糊数模型进行在线插值运算。这种方法是模糊控制的一种改进,它从本质上消除了量化误差和调节死区,还引入了积分因子,克服了以往由于量化误差而引起的稳态误差与稳态颤振现象。
（这个图是从书上直接抄的…）

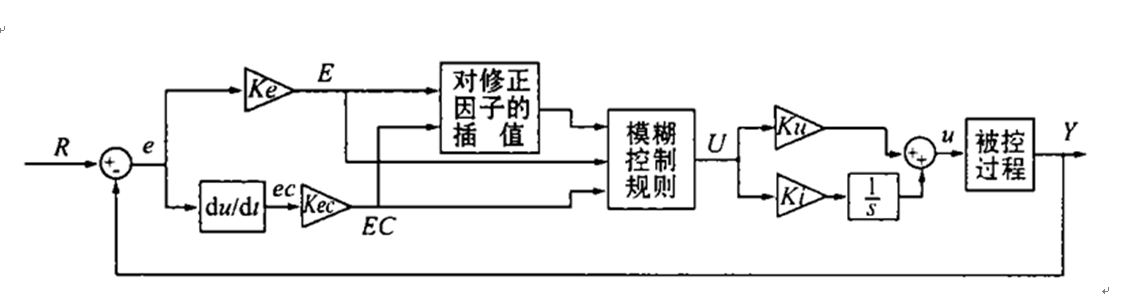
R为系统输入,是俯仰角控制指令;Y为系统输出,是导弹的俯仰角;u为对应舵偏角控制信号;Ke与Kec为量化因子,Ku与Ki分别为比例与积分因子,根据误差E和误差变化率EC对修正因子进行在线插值进而确定模糊控制规则

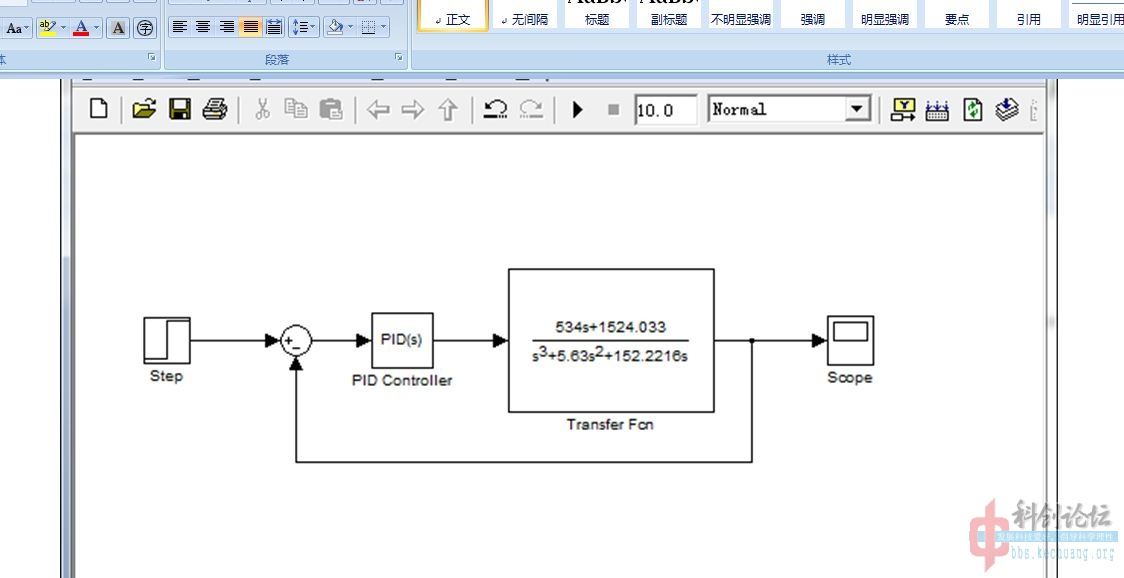
阶跃响应下
gs=tf([534 1524],[1 5.63 152.22 0])
h=tf(1,1)
t=[0:0.01:4]
T=feedback(gs,h,-1);
ys=step(T,t);
plot(t,ys);
只加入Kp，比例系数在分别取0.1、0.3、0.5、0.7、0.9、1、2、3，做出系统阶跃响应图形。
gs=tf([534 1524],[1 5.63 152.22 0])
h=tf(1,1)
t=[0:0.01:4]
for kp=0.2:0.2:2;
T=feedback(kp*gs,h,-1);
ys=step(T,t);
plot(t,ys);
if ishold~=1,hold on,end
end
hold off
（乱吧，乱吧，乱吧…好混乱…）

取Kp=0.5
加入Ki。
Ki=0.05

gs=tf([534 1524],[1 5.63 152.22 0])
h=tf(1,1)
t=[0:0.01:3]
ki=0.005;
kp=0.3;
kpi=tf([kp ki],[1 0])
T=feedback(kpi*gs,h,-1);
ys=step(T,t);
plot(t,ys,'r');
hold on
grid on
gs=tf([534 1524],[1 5.63 152.22 0])
h=tf(1,1)
t=[0:0.01:3]
ki=0.05;
kp=5;
kd=0.07;
kpid=tf([kd kp ki],[1 0])
T=feedback(kpid*gs,h,-1);
ys=step(T,t);
plot(t,ys,'b');
hold on
grid on

Kp=5 Ki=0.05 Kd=0.07(0.5)

好，先就这么多，以上只是MATLAB仿真~实践证明，仿真靠不住……