几何概率是十九世纪末新发展起来的一门学科,使很多概率问题的解决变得简单而不用运用微积分的知识。然而,1899年,法国学者贝特朗提出了所谓“贝特朗悖论”(亦称”贝特朗怪论“),矛头直指几何概率概念本身:
在一给定圆内所有的弦中任选一条弦,求该弦的长度长于圆的内接正三角形边长的概率。
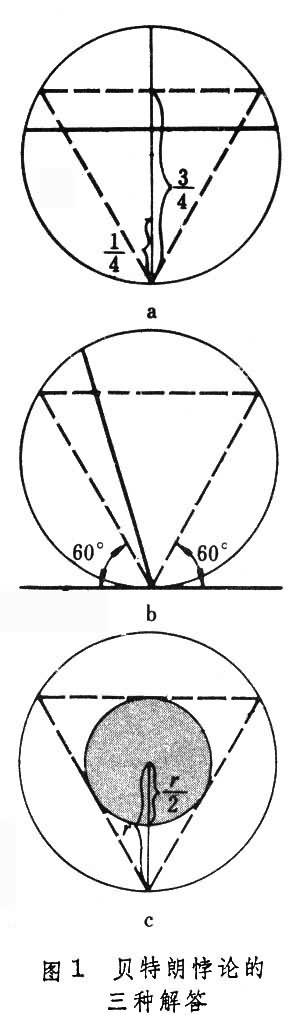
悖论分析 解法一:由于对称性,可预先固定弦的一端。仅当弦与过此端点的切线的交角在60°~ 120° 之间,其长才合乎要求。所有方向是等可能的,则所求概率为1/3 。此时假定端点在圆周上均匀分布。
解法二:由于对称性,可预先指定弦的方向。作垂直于此方向的直径,只有交直径于1/4 点与 3/4 点间的弦,其长才大于内接正三角形边长。所有交点是等可能的,则所求概率为1/2 。此时假定弦的中心在直径上均匀分布。
解法三: 弦被其中点位置唯一确定。只有当弦的中点落在半径缩小了一半的同心圆内,其长才合乎要求。中点位置都是等可能的,则所求概率为1/4。此时假定弦长被其中心唯一确定。
这导致同一事件有不同概率,因此为悖论。
同一问题有三种不同答案,究其原因在于圆内“取弦”时规定尚不够具体,不同的“等可能性假定”导致了不同的样本空间,具体如下:其中“均匀分布”应理解为“等可能取点”。
解法一中假定弦的中点在直径上均匀分布,直径上的点组成样本空间Ω1.
解法二中假定弦的另一端在圆周上均匀分布,圆周上的点组成样本空间Ω2.
解法三中假定弦的中点在大圆内均匀分布,大圆内的点组成样本空间Ω3.
可见,上述三个答案是针对三个不同样本空间引起的,它们都是正确的,贝特朗悖论引起人们注意,在定义概率时要事先明确指出样本空间是什么。
贝特朗悖论在普通高中中模拟概率时会出现。一般第一种答案(即”1/3“)使用较为广泛。
 几何概率是十九世纪末新发展起来的一门学科,使很多概率问题的解决变得简单而不用运用微积分的知识。然而,1899年,法国学者贝特朗提出了所谓“贝特朗悖论”(亦称”贝特朗怪论“),矛头直指几何概率概念本身:
几何概率是十九世纪末新发展起来的一门学科,使很多概率问题的解决变得简单而不用运用微积分的知识。然而,1899年,法国学者贝特朗提出了所谓“贝特朗悖论”(亦称”贝特朗怪论“),矛头直指几何概率概念本身:
200字以内,仅用于支线交流,主线讨论请采用回复功能。