2. 耦合度和频率分裂。
上面说到了没有次级,电流会无限制增大。
这怎么行呢!于是就有了次级~
凭直觉,次级放的离初级近,和次级放的离初级远肯定是有区别的对吧,
量化这个参数,就是传说中的耦合度k。
0≤k≤1,表征初级发出的磁场有多少能被次级接收到。
现在加上这个传说中的次级,再来仿真看看:
![High_dI_dt_with_sec_high_k.png]()
![High_dI_dt_with_sec_mid_k.png]()
看出来没有?
1.高耦合率的电流最大值比较小。
2.高耦合率达到极大值快,就是上面那个“包络线”震动的比较快。
这里先引用两个图:
![changek.gif]()
![doubhump.gif]()
这就是说明,在有次级的情况下本来单一的频率(LC谐振频率)会分离成两个峰。
而知道点物理的人都懂得,这两个频率之差俗称拍频,也就是包络线波动的频率
根据某公式,
f1=f0/√(1-k),
f2=f0/√(1+k),是两个峰的频率。
所以,耦合度k越高,频率之差越大,自然“抖动"也快了。
![High_dI_dt_with_sec_mid_k_FFT_freq_split.png]()
![High_dI_dt_with_sec_high_k_FFT_freq_split.png]()
这分别是上面两个图的傅里叶频谱,可以清楚的看出频率分裂的差别。
那么耦合度对电流上升速率有没有影响呢?显然是有的。
不仅仅是电流极大值的位置和大小会变,
耦合度高了的时候,就相当于初级谐振被次级限制住了,所以上升也会减慢。
这里有个我很喜欢的图来解释耦合度:
![coupling.gif]()
所以到这里,耦合度和Z因子就说完了。
后面会讲到S路线要说到这个。
要电流上升速率快的话:
1. 减小Z因子,即增大C减小L
2. 或者减小k
但是注意!
k太小了,就像没有次级一样,电流会无限增长,管子果断归西。。
k太大了电弧短额。。虽然对管子好些。
还没完待续~
上面说到了没有次级,电流会无限制增大。
这怎么行呢!于是就有了次级~
凭直觉,次级放的离初级近,和次级放的离初级远肯定是有区别的对吧,
量化这个参数,就是传说中的耦合度k。
0≤k≤1,表征初级发出的磁场有多少能被次级接收到。
现在加上这个传说中的次级,再来仿真看看:
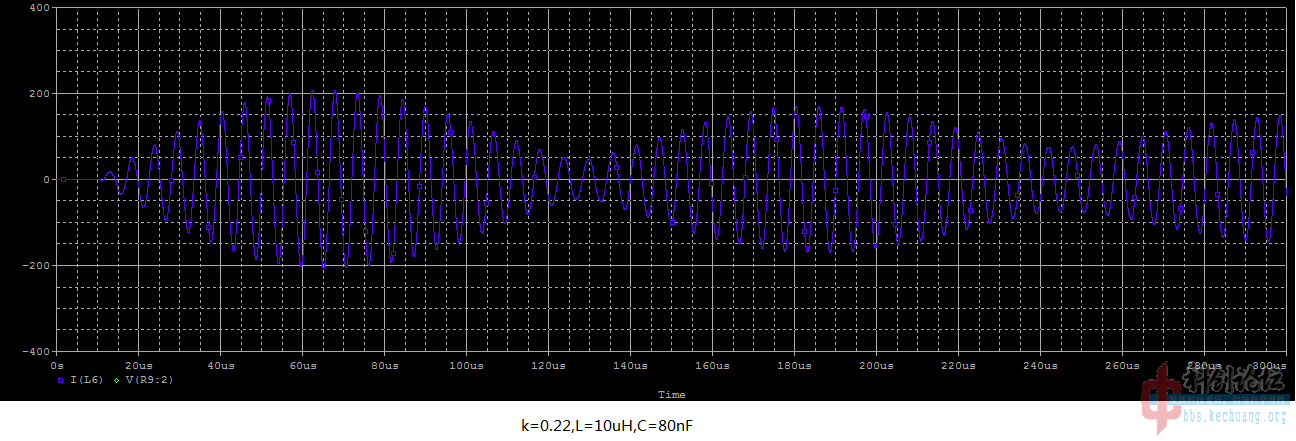
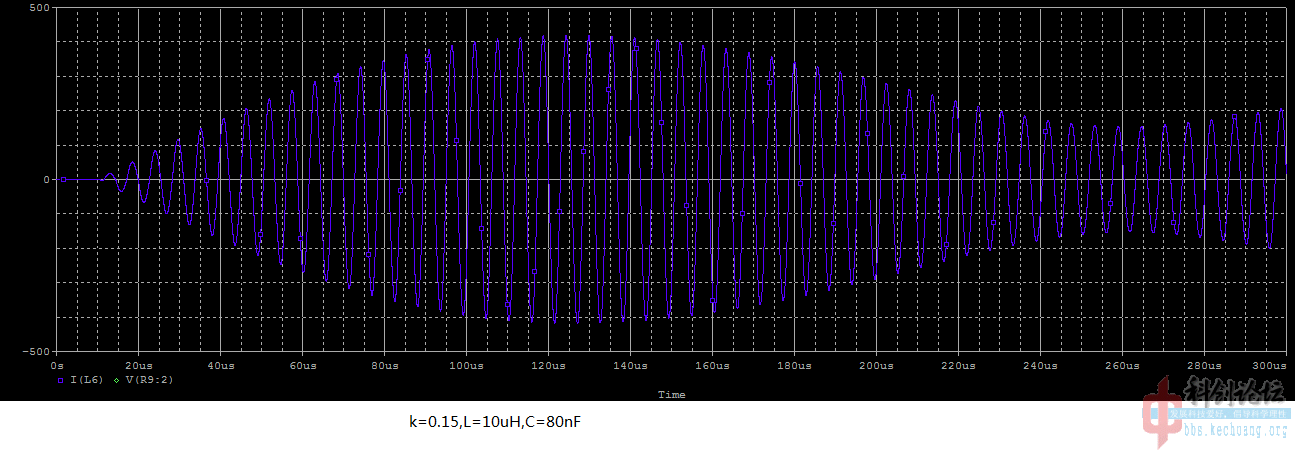
看出来没有?
1.高耦合率的电流最大值比较小。
2.高耦合率达到极大值快,就是上面那个“包络线”震动的比较快。
这里先引用两个图:

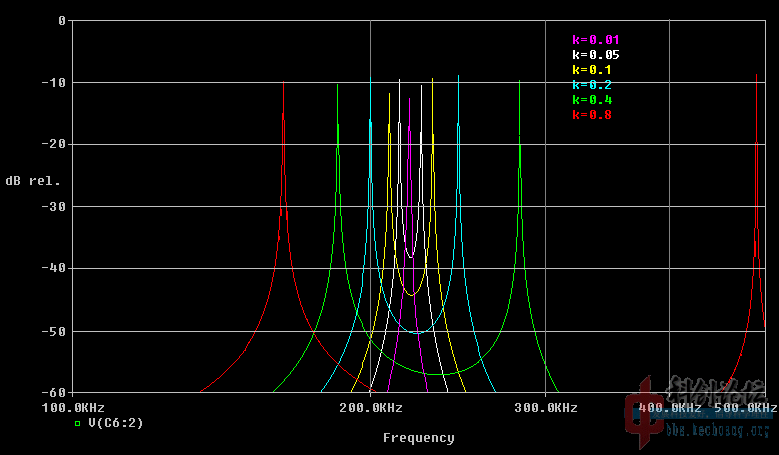
这就是说明,在有次级的情况下本来单一的频率(LC谐振频率)会分离成两个峰。
而知道点物理的人都懂得,这两个频率之差俗称拍频,也就是包络线波动的频率
根据某公式,
f1=f0/√(1-k),
f2=f0/√(1+k),是两个峰的频率。
所以,耦合度k越高,频率之差越大,自然“抖动"也快了。
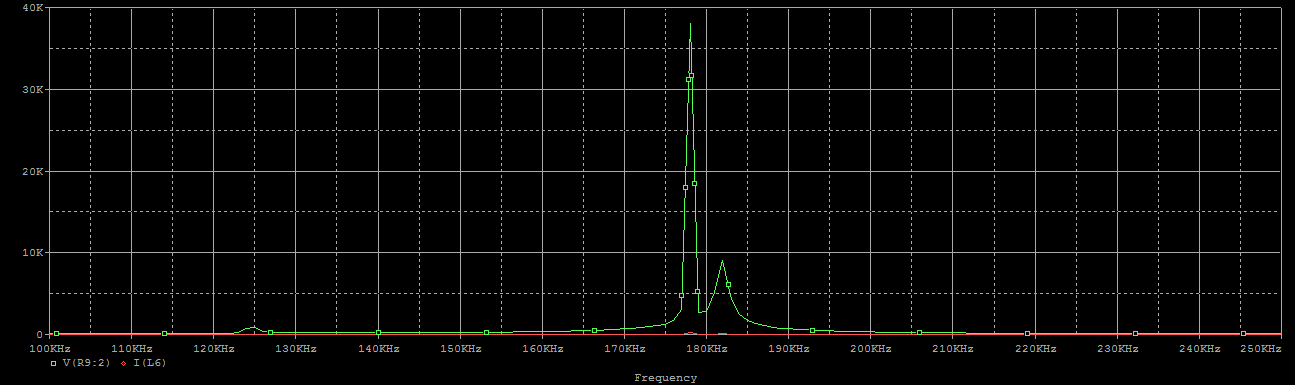
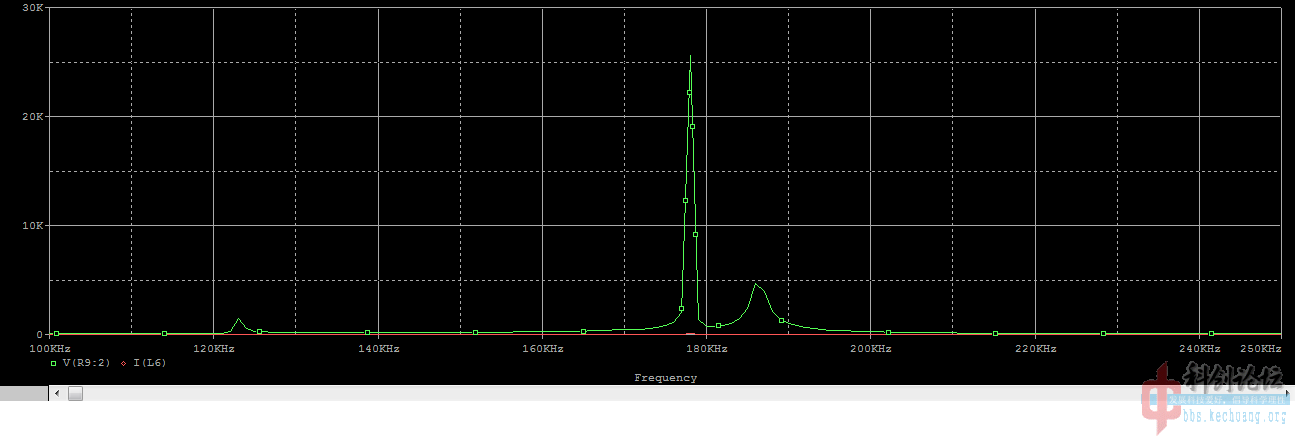
这分别是上面两个图的傅里叶频谱,可以清楚的看出频率分裂的差别。
那么耦合度对电流上升速率有没有影响呢?显然是有的。
不仅仅是电流极大值的位置和大小会变,
耦合度高了的时候,就相当于初级谐振被次级限制住了,所以上升也会减慢。
这里有个我很喜欢的图来解释耦合度:

所以到这里,耦合度和Z因子就说完了。
后面会讲到S路线要说到这个。
要电流上升速率快的话:
1. 减小Z因子,即增大C减小L
2. 或者减小k
但是注意!
k太小了,就像没有次级一样,电流会无限增长,管子果断归西。。
k太大了电弧短额。。虽然对管子好些。
还没完待续~
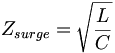




200字以内,仅用于支线交流,主线讨论请采用回复功能。