看来lz对LATEX的使用不太熟啊，分数的代码是\frac{}{},能用分数的就别打个斜杠了。
文中可以这么写：
p+ρgh+\frac{1}{2}ρv^2=C
$$p+ρgh+\frac{1}{2}ρv^2=C$$
\sqrt{\frac{2G}{Sρ}+v}=v_2
$$\sqrt{\frac{2G}{Sρ}+v}=v_2$$
90616
%7B%22isLastPage%22%3Atrue%2C%22notes%22%3A%5B%5D%2C%22pid%22%3A%22938503%22%2C%22tid%22%3A%2290616%22%2C%22mainForumsId%22%3A%5B%22165%22%5D%2C%22categoriesId%22%3A%5B%5D%2C%22tcId%22%3A%5B%5D%7D
%7B%22isEditMode%22%3Afalse%7D
一种简单的设计航模机翼的方法
中文摘要
一种简单的设计航模机翼的方法
（2年前就已经在科创潜水了，当时更多在关注火箭版，无奈没有制作火箭的条件，只能跑到这里来了，反正不管航模还是火箭，只要能飞的我都感兴趣）
第一篇文章，不知道有没有人发过重复内容如有错误或重复请指出或刪除
我知道大部分人都用模拟软件来设计航模，但作为贫穷的学生党，我连电脑都没有，于是想出了下面的主意来设计机翼。
在伯努力定理中，1/2ρv*2为动能，ρgh为重力势能， p为压力势能
$$p+\rho gh+1/2\rho v^{2}=C$$ $$p_{2}+\rho gh+1/2\rho v_{2}^{2}=C$$
C为常数,p为机翼上方压强，p2为机翼下方压强，v为机翼下方气流速度（飞机速度），v2为机翼上方气流速度，G为飞机总重，S为机翼下表面面积（待会儿详细说），ρ为空气密度，v2大于v大于0，p2大于p，則可得
$$p+\rho gh+1/2\rho v^{2}=p_{2}+\rho gh+1/2\rho v_{2}^{2}$$
移项并合并
$$p-p_{2}=1/2\rho (v_{2}^{2}-v^{2})$$
其中$p-p_{2}$即为$\Delta p$
对应的，$\Delta p=G/S$
所以最终变形为
$$\sqrt{2G/S\rho+v}=v_{2}$$
将自己航模的参数代入（G，S），空气密度代入（$1．29kg/m^{3} $ ），就得到一个函数，在函数中取的v，v1值的差即为气流走过的路程差，也相当于机翼上下面积差，这样就能设计机翼上表面了.
另外，机翼下表面默认为平面，计算时代入的G是设计之前的总重，也就是说机翼这部分的重量计算时得考虑一下(其实影响也不大)。S本來应该是机翼中部截面面积（如图），但我觉得换成下表面的话也一样
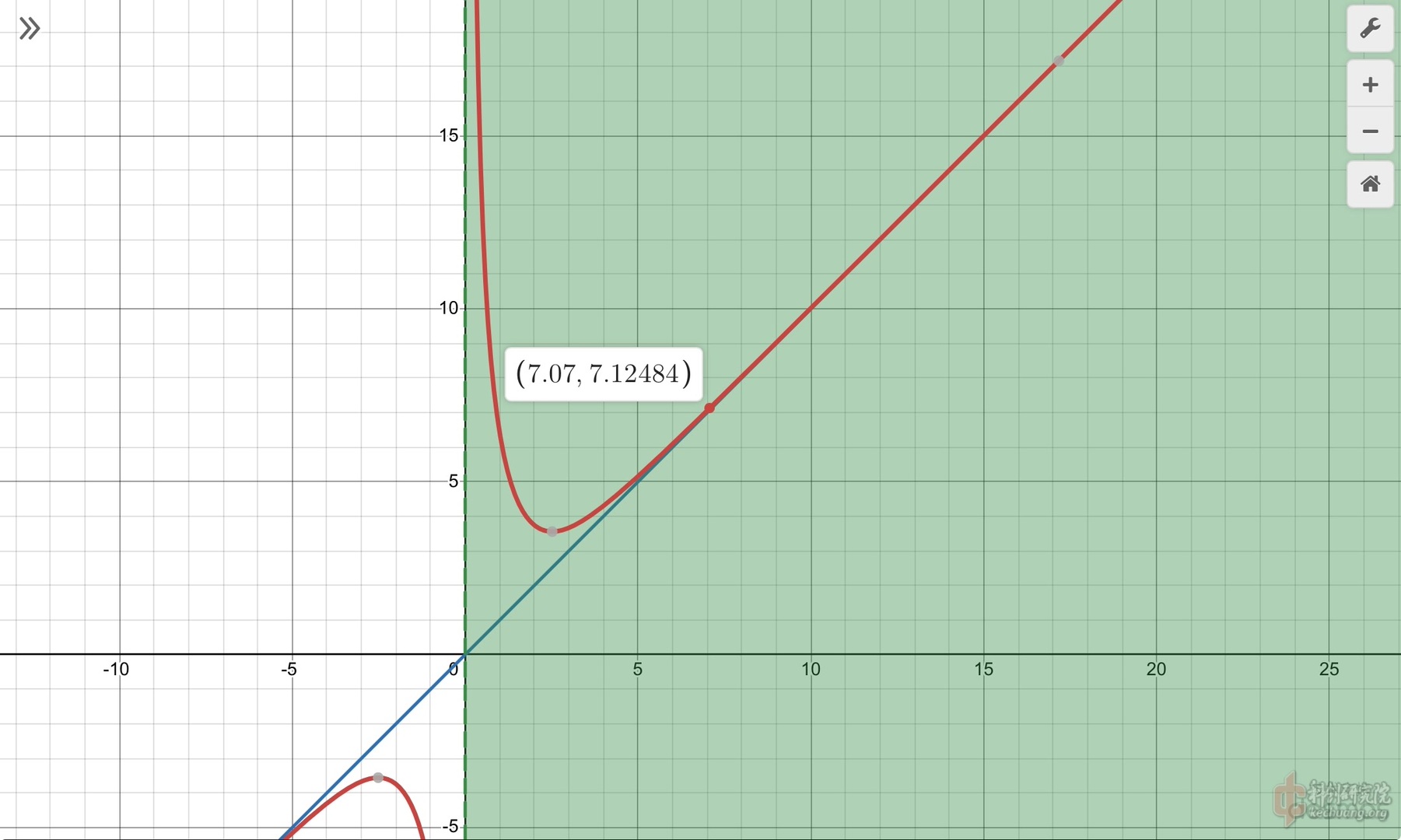
下面举个例子：某初三学生制作了一台矩形翼简单航模，测得G =2 N，S =0．12$m^{2}$,而空气密度为$1．29kg/m^{3}$他就能得到$$\sqrt{25．839+v}=v_{2}$$
函数图像就是这样的（绿的是取值范围）
取v值为5.54m/s，则v2值为5.6017m/s
上下翼面截面长度差为6.17厘米．
这种方法靠不靠谱我还不太了解，不过凑合用还是可以的。
另外也顺便得出了飞机飞行速度为5.54米每秒，然后就该考虑动力系统了^
[修改于 1个月2天前 - 2024/10/20 15:03:29]
糾正一下文中公式，$$\sqrt{\frac{2G}{Sρ}+v^2}=v_2$$
引用
加载评论中，请稍候...
200字以内，仅用于支线交流，主线讨论请采用回复功能。
这是修正过的图像
可以看到速度越快，v2，v差值越小
引用
加载评论中，请稍候...
200字以内，仅用于支线交流，主线讨论请采用回复功能。
Bro,c = $\frac{F}{Sq}$
=$\frac{2F}{(\rho v^2)}$
就是$\frac{2F}{\rho v^2S}=\frac{\rho(v_2^2-v^2)}{2}$ （能这么替换吧）
我把q中的动压的气流速度理解成v，F近似理解成G，再变化就成了$$v_2=\frac{\sqrt{\frac{4G+v^4\rho^2S}{S}}}{\rho v}$$相当复杂，简直不知道是对还是错了
此时再代入例数据，则有
数据看起来挺合理
另外动压是对与空气流动方向垂直或斜交的平面施加压力，所以是机翼前缘受压，并且压力作用方向与水平面存在一定角度？
引用
1
加载评论中，请稍候...
200字以内，仅用于支线交流，主线讨论请采用回复功能。
楼主的理论推导存在少量问题，“C为常数,p为机翼上方压强，p2为机翼下方压强，v为机翼下方气流速度（飞机速度），v2为机翼上方气流速度，G为飞机总重，S为机翼下表面面积（待会儿详细说），ρ为空气密度，v2大于v大于0，p2大于p”从这一段就可以看出楼主采用的是大多数初高中物理教学用烂了的等时理论（Equal Transit Time Theory）。它假设空气在机翼上方和下方同时到达机翼后缘，这是不正确的。实际上，空气在机翼上方的流动路径较长，流动时间也更长。而且忽略了空气的粘性效应和边界层的影响（而且对于机翼上下翼面保持水平的纸飞机的升力原理就无法解释）
正确的升力解释要涉及到库塔-儒科夫斯基定理$L=\rho v\Gamma$和边界层理论：真实的升力应该由机翼的环量$Gamma$决定。不过对于简单翼型、低速飞行的小型模型飞机等时理论可以作为一个近似解。具体的可以看一看NASA的David Anderson博士撰写的一篇论文《How Airplanes Fly: A Physical Description of Lift》。
引用
1
加载评论中，请稍候...
200字以内，仅用于支线交流，主线讨论请采用回复功能。
针对上述讨论进行总结
对固定翼航模上下翼面的设计进行初级分析，得出较简单的理论，或许能作为简单翼型、低速飞行的小型航模的近似解（感谢各位大佬批评指导）。
$$\sqrt{\frac{2G}{Sρ}+v^2}=v_2$$这是公式
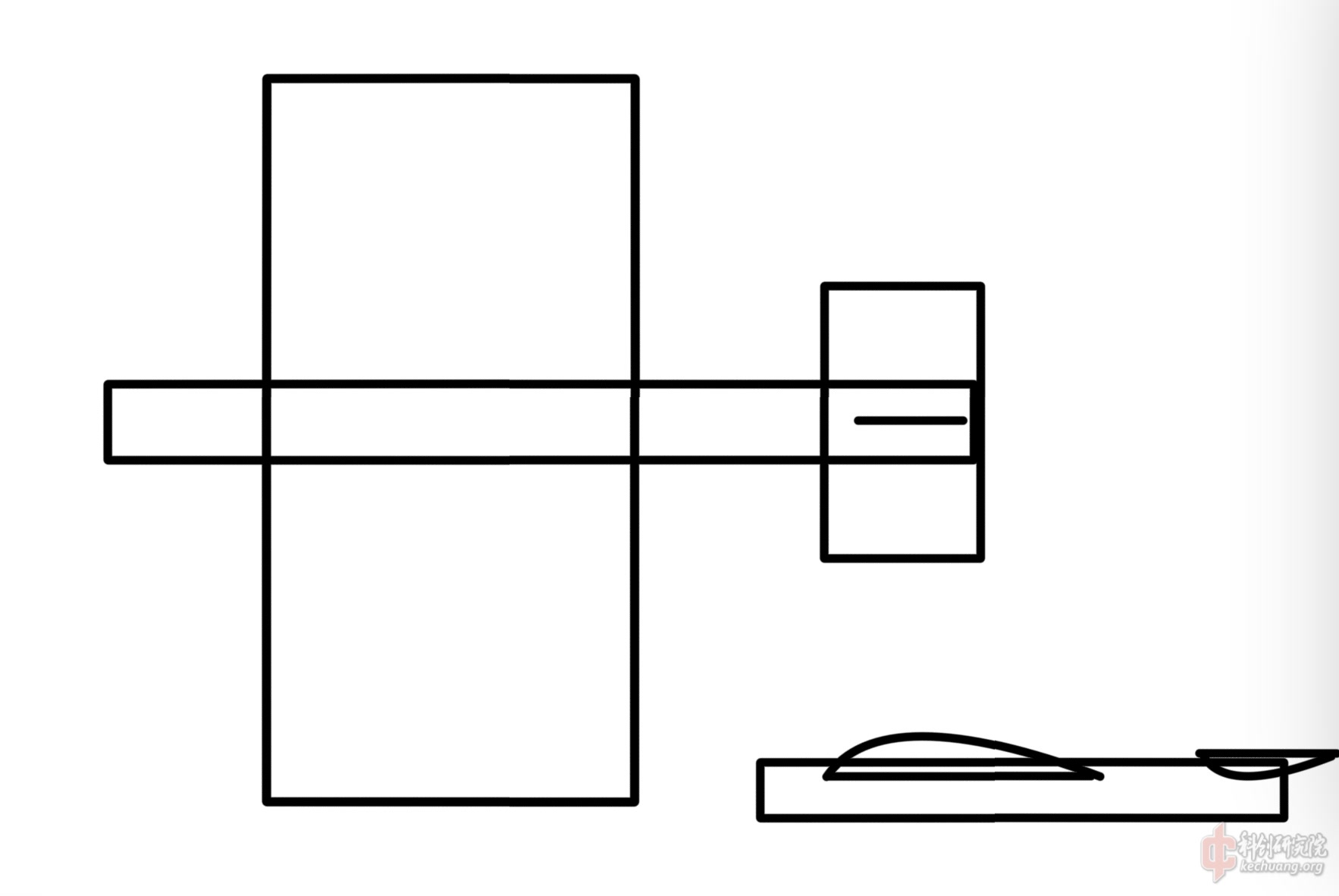
图中的航模翼面面积为0.12$m^2$（翼长60cm，翼宽20cm)，质量0.15kg
代入得
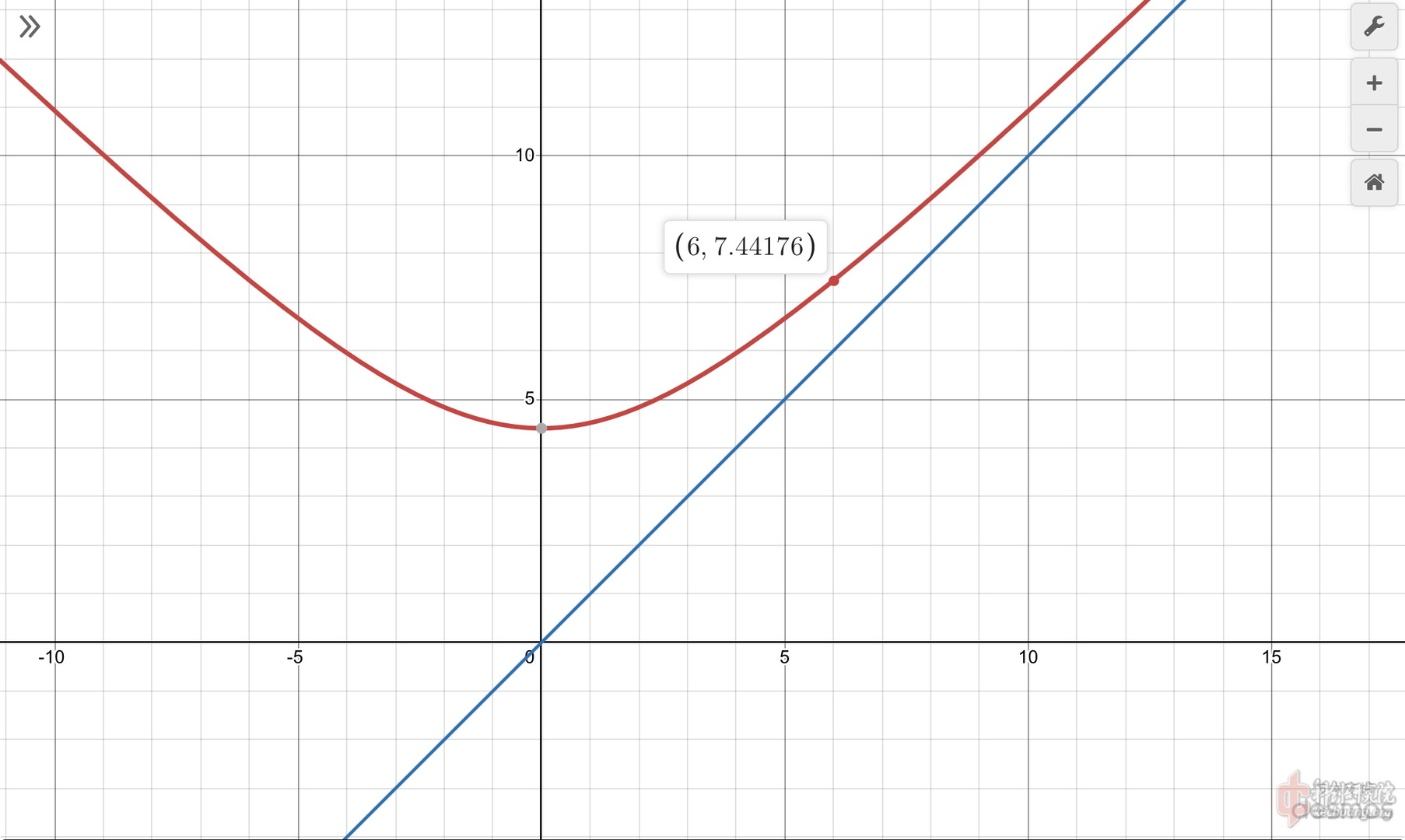
v2:v=6:7.44176，计算得当下翼面横截面长为20cm时，上翼面为24.805cm
这个是近似解
引用
加载评论中，请稍候...
200字以内，仅用于支线交流，主线讨论请采用回复功能。