要进行估测,一定要作出一些假设。这就好比,要计算两辆火车相向而行从相遇到离开的时间,你必须假设它们是匀速行驶的,而且互不干扰……如果没有这些假设的前提,就无法进行估算。
假设电机,以及/或者与电机相连的机械结构,惯量很大。这样,便可以假设任意时刻其加速度接近于0,速度基本不变。
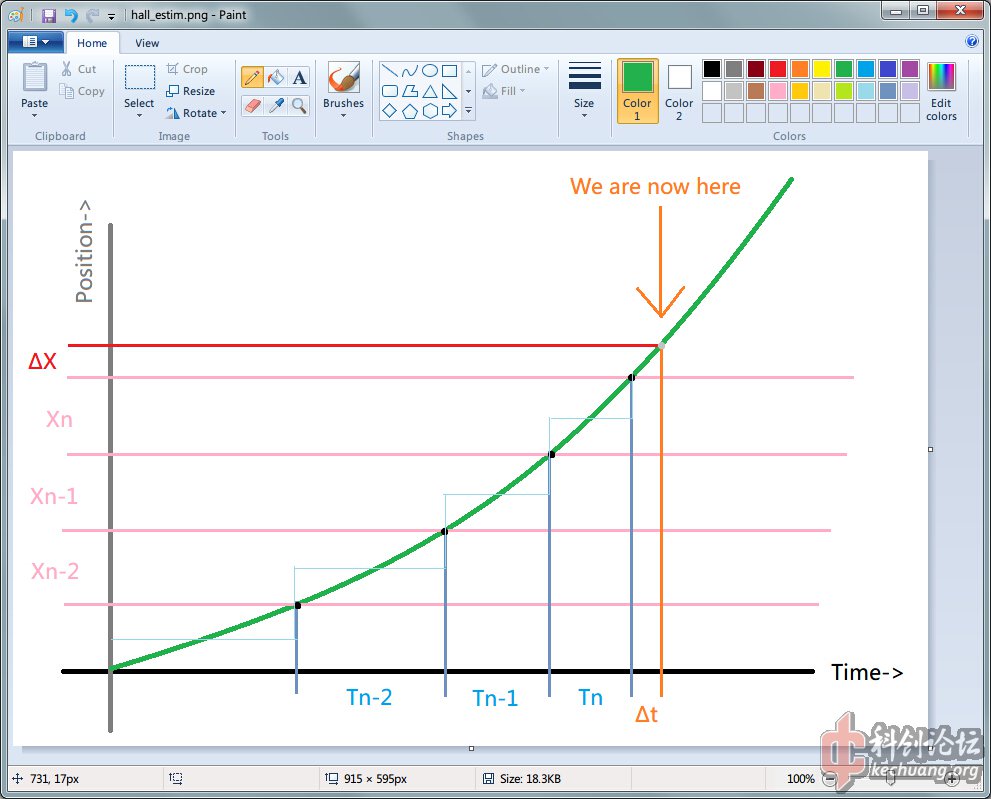
设速度不变,因为速度是距离和时间的比值,可以得到以下公式:
ΔX / Δt = Xn / Tn
ΔX = Δt * Xn / Tn
这真是太简单了!
前提是,上一时刻和这一时刻的速度基本不变。假如加速度为0,这个算法就是合适的;假如加速度是一个不可忽略的值,这个算法就会产生误差。
![QQ截图20150901162604.jpg]()
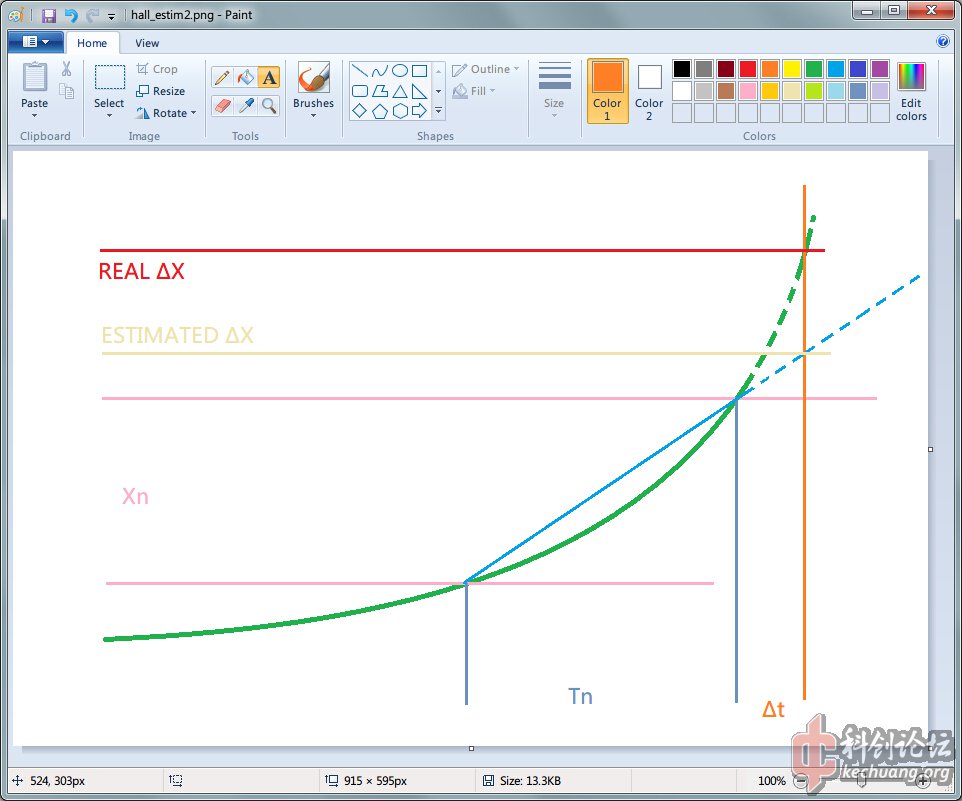
上图:
天蓝色为一条斜率不变的直线,代表假设速度不变。
由于电机正在加速,蓝线和绿线产生了分歧,在t时刻,电机的实际位置(红线)比算法估测的位置(米黄色线)要更远一些。但如果在两个脉冲边沿之间电机速度变化不大,这个估测还是相当准确的。
假设电机,以及/或者与电机相连的机械结构,惯量很大。这样,便可以假设任意时刻其加速度接近于0,速度基本不变。
设速度不变,因为速度是距离和时间的比值,可以得到以下公式:
ΔX / Δt = Xn / Tn
ΔX = Δt * Xn / Tn
这真是太简单了!
前提是,上一时刻和这一时刻的速度基本不变。假如加速度为0,这个算法就是合适的;假如加速度是一个不可忽略的值,这个算法就会产生误差。
上图:
天蓝色为一条斜率不变的直线,代表假设速度不变。
由于电机正在加速,蓝线和绿线产生了分歧,在t时刻,电机的实际位置(红线)比算法估测的位置(米黄色线)要更远一些。但如果在两个脉冲边沿之间电机速度变化不大,这个估测还是相当准确的。

200字以内,仅用于支线交流,主线讨论请采用回复功能。