
近来广受关注的矢量控制,是以电机为控制对象的PWM 电路驱动方法。不足之处是,要增设传感器。本文介绍利用瑞萨RX62T 低压电机控制评估系统实现矢量控制的实例。
这种方法是以坐标变换为中心的数学方法,所以文中会出现很多矩阵。
何为矢量控制
使电机达到最大转矩的电流控制
矢量控制通过电流控制使电机达到最大转矩,是让电机效率最大化的控制,即:在电流相同情况下,让电机的转矩达到最大。具体内容如下。
① 将电机的电流矢量分解为励磁电流分量和转矩电流分量,分别加以控制。
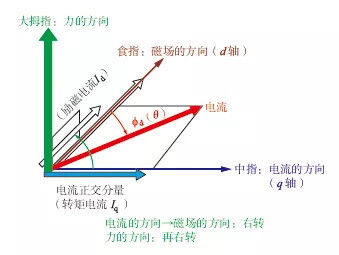
②通过控制电机的电压和相位,调整磁通和电流相位,以实现最大转矩。
实际上是,将3 相固定坐标系电机模型转换为2 相旋转坐标系电机模型,使磁场和转矩转换为线性矢量并分别进行控制,如图1 所示。

图1
也就是,让转子产生的磁场与线圈产生的磁场形成产生最大转矩的90°电角度(适用于SPM 电机),变成对转矩分量(纯电流)的控制,是与直流电机一样的线性控制”。
使用数学方法的理由
“矢量控制”听起来很简单,实际上是一个很复杂的过程,如图2 所示。

图2
定子的线圈是三维的(U 相/ V 相/W 相),而转子的永磁体是旋转的二维(N 极/ S 极)。在电流相同的情况下,计算出最大转矩是很困难的。因此,将3 相线圈变换为二维(2 相),并将其模型看作直流电机模型。在计算中,尽可能最小化不形成转矩的电流分量。将计算结果还原到3 相时,为了让电流达到目标值,将施加到各层的电压转换为通过定时器控制的PWM 输出占空比。
控制方式
矢量控制的基础是洛伦兹力。
将电机模型化
将电机转化为模型(驱动电压方程)来表示,如图3 所示,它是线圈电阻上的电压,与 电感及磁链产生的感应电压之和。
通过线圈的总磁通
磁链,也就是通过线圈(导体)的总磁通,如图4 所示,

图4
是下述两者之和:
·线圈电感产生的磁通
·转子的永磁体产生的磁通
另外,计算对象中也包括各相线圈之间互感所产生的磁通。由图3、图4 可以推导出图5 所示的各相的电压方程。

图5
将电压3 相坐标系变换为2 相旋转坐标系
从3 相固定坐标变换为2 相旋转坐标,分两个阶段(图6)。

图6
① 3 相UVW 坐标→ 2 相固定坐标αβ。
② 2 相固定坐标αβ → 2 相旋转坐标dq。
各阶段的坐标变换矩阵如图7 所示。

图7
三维坐标变换为二维坐标
如前所述,坐标变换的目的是,让转子产生的磁场与线圈产生的磁场形成90°的电角度,进而形成最大转矩。
(1)αβ 变换
与U 轴重合的是α 轴,β 轴与α 轴成90°(分别为固定轴)。
(2)dq 变换
dq 变换中,N 极为d 轴,q 轴与d 轴成9 0 °。变换后的电压模型用dq 轴表示,如图8 所示。

图8
从图可见, 模型中的交流成分不见了, 说明dq 上的电流在2 相旋转坐标系中可分别适用于直流控制。而表面式永磁同步电机(SPMSM,略称为SPM电机)无论在2 相旋转坐标系中的什么位置,电感都是不变的,即Ld = Lq(图9 ),

图9
如“CQ 无刷电机”。市售的EV(包括混合动车),一 般使用的是内置式永磁同步电机(IPMSM,略称为IPM 电机),其永磁体是嵌在转子中的。
转矩的控制
转矩如何变化
矢量控制的目的是改变转矩。下面, 我们来看看转矩的表现形式及相互关系。转矩是由电流产生的,其计算公式如图1 0 所示。

图10
因为转矩N 是力矩(沿半径r 转动的力F),所以用矢量表示为N =r×F。图10 中出现了两种类型的转矩。a 电磁转矩:永磁体与定子线圈之间的力所产
生的转矩。b 磁阻转矩:转子磁阻的异向性(凸极作用)产生的转矩。在S PM 电机中,Ld = Lq,磁阻转矩为0 ,只要对q 轴的电流进行控制,就能控制转矩(图11)。
图11
因此,将d 轴电流指令值变为0,就能对转矩与q轴电流进行线性控制。
去除感应电压项—非干涉控制
当电压模型转换为电流模型时,q 轴的电流模型中包含了d 轴的项目,特别是与ω 成正比的项目,即干涉项。这意味着,高速转动时永磁体产生的感应电压增大,随之干涉项产生的不良影响也将扩大,导致控制性能变差。将消除项也纳入计算范围的方法叫做“非干涉控制”(图12)。

图12
非干涉控制的PI 速度控制框图如图13 所示。

图13
1
END
1
往期精彩