<figure> </figure>

电机的容量与体格“电机容量”与“输出功率”相同?
在表示电机规格的术语中，我们会使用到“电机容量”这个词。一般情况下，电机容量被认为是电机的输出功率。但是，输出功率的单位是 W（瓦特），而电机容量的单位是kV·A（千伏安）。严格意义上讲，这两个术语所包含的意义是不同的。在本书中也曾经提到，改变施加给电机的电压和线圈导线规格，会导致电机的输出功率发生很大的变化。例如，“CQ 无刷电机和逆变器套件”中的电机，其输出功率的可调节范围是50W ～ 3kW。这个范围虽然也是电机的一个指标，但我们需要另一个指标来表示电机本身所具备的潜力。这个指标就
是电机容量。电机比容量= 电机容量÷ 转速有的文献中使用了“（电机）比容量”一词（《电气工程学手册》，欧姆社）。电机容量除以电机转速就得到电机比容量［kV·A/$ r/min$］。我们用电机比容量来表示刚才提到的电机本来具备的潜力，理解起来会更容易一些。
综上所述，即使是同样的电机，通过调整参数，它的输出功率就会发生很大的变化。而且，无一例外都提高了转速。这里顺便提一下，电机的体格（大小）也决定了电机的转矩。因为提高电机功率就是要提高电机转速。也就是说，无论怎么调整，使得电机的输出功率增加或减少，但平均到每转上的容量，如果用“比容量”来考虑，电机的潜能几乎是不变的。举例来说，就像发动机的排气量。即使是排气量相同的发动机，也可以通过调整改变其输出功率。从大的方面来理解，就是排气量与发动机特性的关系。改变电机的体格（大小），电机容量会发生什么样的变化？电机所具有的潜能究竟是什么？如果这个潜能真的存在，它与电机的体格又是怎样的关系？接下来，我们来研究电机容量与电机体格之间的关系。关于电机体格与电机容量的关系，可以在很多文献或书籍中找到相应的讲解（如：《电机设计学》，竹内寿太郎，欧姆社）。
在这里，笔者以上述书籍中多达两三页的内容进行整理，并在此基础上加入前面反复提到的“电负荷”“磁负荷”，以期能让读者更清楚明了地理解相关的内容。改变电机的体格：将各部分的尺寸变为原来的2 倍我们来看看改变电机体格的具体实例。首先，我们将电机各个组成部分的尺寸（长、宽、高）变为原来的2 倍（图3）。

<figure> </figure>

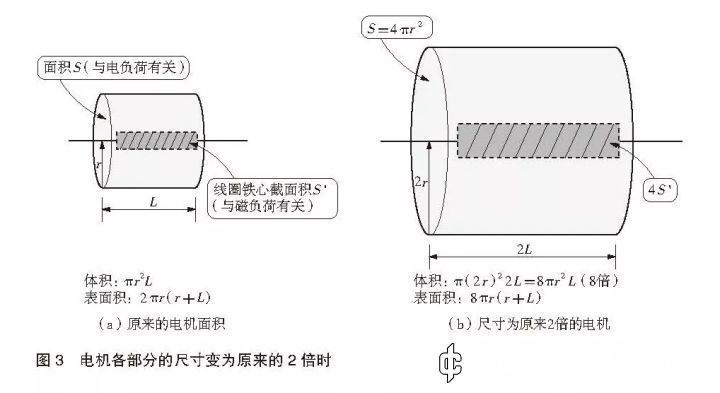
电负荷铁心尺寸变为原来的2 倍，也就是说铁心面积为原来的4 倍，可以用于绕线的空间也变成了原来的4 倍。假设线圈匝数保持不变，线圈截面积变成原来的4 倍，在电流密度不变的情况下，流过线圈的电流是原来的4 倍。也就是说，电机的电负荷为原来的4 倍。磁负荷电机尺寸变为原来的2 倍，铁心的截面积变为原来的4 倍。如果电流密度和通过铁心的磁通密度不变，则铁心通过磁通的能力为原来的4 倍。电机的磁负荷也为原来的4 倍。由以上可知，与原来相比，尺寸变为2 倍的电机，它的输出功率（准确来说应为电机具备的输出功率的潜力，即容量）为4×4=16 倍。也就是说，10kW的电机，如果尺寸变为原来的2 倍，输出功率就会变成160kW。当然，电机各部分的尺寸变为原来的2 倍的话，它的体积为原来的2×2×2=8 倍。电机的体积变为原来的8 倍，在各个部分材料不变的情况下，电机的质量、材料成本应该也是原来的8 倍。也就是说，我们用8 倍的材料，获得了16 倍的电机容量。这很划算吧？为什么电机的体格越大，效率越高？电机的体格变为原来的8 倍，那么它的损耗会发生什么样的变化？　假设它的铜损和铁损不变（因为电流密度、磁通密度没变），则电机的损耗与质量也是原来的8 倍。到这里，我们知道：电机容量（功率）增加到16 倍，电机损耗增加了8 倍。因此，电机的体格越大，效率就越高。这也是工业电机大部分又大又重的原因。同时也可以解释为，电机越大、越重，就越容易获得高效率。EV 用电机并不具备体格优势?电机的体格越大，效率越高。那么，EV 上使用尺寸更大的电机不就可以了吗？这里，汽车用电机与EV 用电机的区别就出现了。前面我们就提到过，搭载在汽车上的电机，它本身的质量会消耗能量。因此，就算电机的效率再高，质量增加导致能量消耗增加，大体格的电机并不适合搭载在汽车上。电机的种类有很多，在某种意义上也可以说，汽车用电机都是经过特别设计的。也可以说，正是因为汽车用电机存在体格、形状、质量等诸多限制，才在这诸多限制中获得了进化。大体格电机的发热问题电机体格越大，效率越高。同时，也存在发热的问题。各部分尺寸为原来2 倍的电机，其表面积为原来的2×2=4 倍，散热面积也是原来的4 倍。这是一个严峻的问题。想一想看，电机容量为原来的16 倍，损耗（发热）为原来的8 倍，而散热面积只有原来的4 倍。很明显，电机的冷却是不充分的，电机温度会升得更高。因此，为了应对电机的发热，就需要增加散热风机或者水冷设备等。尽管如此，电机的散热问题依然是一个课题。电机的外径、轴长、容量外径与轴长以及D 2L 说与D 3L 说电机是一个拥有悠久历史的装置，但直到现在仍然有很多谜题未解。与天文学中的“三体问题”一样，电机涉及电、磁、力学三大与能量相关的问题，它们之间的关系错综复杂。在这里，我们来探讨一下与电机体格/ 容量相关的话题。说到电机体格，重要的并不是体积容量。因为，即使体积容量相同，也还存在外径与轴长两个影响要素。在电机领域，存在着D 2L 说：电机的容量与直径（准确地说，应该是电机的转子与定子之间存在
的气隙的直径）平方成正比，与轴长（准确地说，应该是铁心的长度）成正比。实际上，还存在着D 3L说。笔者认同的是后者。但是，这又与电机的种类和容量有关，并不能断言哪种说法正确，哪种说法不正确。从笔者使用过的电机来看，更接近D 3L 说。这是一个很有趣的话题，下面结合电机的体格问题（直径、轴长）进行简单说明。改变电机的体格：改变直径与轴长● 直径为原来的2 倍，轴长不变时

<figure> </figure>

图4（a）与（b）显示了电机体格的差别。首先，我们从电负荷与磁负荷的角度来推理。直径为原来的2 倍时，电负荷为原来的4 倍。再来看磁负荷，直径变为原来的2 倍，铁心的截面积（磁路的截面积）在径向上变为原来的2 倍，在轴向上面积不变。也就是说，磁负荷变成了原来的2 倍。电机容量变为4×2=8 倍。直径不变，轴长为原来的2 倍时接下来，我们让直径保持不变，将轴长变为原来的2 倍［图4（c）］。这就是笔者制作电机时经常使用的“积厚向上”方法。这种情况下，电机容量会发生怎样的变化？首先，电负荷因直径不变而不会发生改变（因为绕线空间不变）。磁负荷因轴长变为原来的2 倍（磁路截面积为原来的2 倍）增至原来的2 倍。因此，电机容量为原来的1×2=2 倍。综上所述，电机容量与D 3L 成正比。当然，我们也同样要考虑电机的散热措施。对D 2L 说的考察：对象电机不一样？前面提到，电机容量与D 3L 成正比。而一般情况下，D 2L 说更占主流。推测其原因，就在于电负荷的计算方法不同。在以往的有刷电机及感应电机上，绕线空间在某种意义上是被限定的。例如，在有刷电机上，即使直径变成了原来的2 倍，绕线空间也不会简单地就变成原来的4 倍。因为在有刷电机上，铁心圆周方向上的尺寸虽然可以变成原来的2 倍，但是径向尺寸几乎是改变不了的。另外，感应电机也一样。在分布式线圈中，嵌线深度过大导致连接线增加。这除了会引起的弊害（质量、体积增加，效率降低），还会引起线圈感应出现差异（距离铁心中心越近的线圈比距离表面越近的线圈的感应更强）等问题。还有，工业领域中使用的大型电机也是一样的。即使加大了转子的直径，线圈还是安装在靠近其表面的位置为好。这就使得电机在圆周方向上变大，而在径向上几乎不变。这样一来，电负荷就不是与D 2 成正比，而是与D 成正比了。同时，磁负荷也与D 成正比。因此，变成了容量N 与D 2L 成正比．就电机的规模（体格）而言，如果以笔者使用过的无刷电机（同心绕线）为考察对象，则D 3L 说更有说服力。电机容量与电机体格的关系有着诸多学说《电气工程学手册》（日本电气学会编）记载的名为输出功率方程的公式中，也有关于电机容量的内容。详情如下：

<figure> </figure>

式中，N 表示输出功率（kW）或容量（kVA）；D 、L 分别表示电枢铁心直径、长度（m）；K 、K '、K "表示各种学说的输出系数。关于输出系数，其变化趋势如图5 所示。

<figure> </figure>

式（1） 为D 2L 说， 式（2） 为D 3L 说。通过对图5 中两种学说的比较可知，比容量小的区域内（小型电机）D 3L 的系数基本不变，D 2L 的系数变化幅度大；相反，在比容量大的区域（大型电机）内，D2L的系数变化幅度反而变小了。式（3）是对两种学说进行改良后得到的，它能套用在不同的电机上，可
以认为在某一区域内具有通用性。这段描述也是笔者推荐D 3L 说的根据所在。
1END1往期精彩

钴，一只随时都可能掐死电动汽车产业的手【锋芒】电动汽车时代，新“石油”来临
【丰田开放23740项汽车专利事件】调查电动汽车背后藏着——石油、战争、地缘政治
6分钟完成充电，续航320km——东芝TNO/NCM电池初探老铁，

来杯特斯拉专利文献不，电磁口味的【日本庆应大学、群马大学数据】EV与燃料车的能量效率对比