同飞动专业学弟双手支持赞同
研发设计一款飞行器是一项系统工程,涉及多学科交叉理论,并且在大量试验和测试中总结了较多的经验公式,目前针对主流飞行器已基本形成了比较完备的设计思路和方法,相关的参考文献和书籍已基本普及。飞行器设计在国内各高校学科门类中属于航空宇航科学与技术大类,涵盖力学、控制、电子信息等一级学科,具体又包含气动、结构、控制、制导、动力等多个子课题。我们希望借平台的力量逐渐向大家普及与飞行器设计相关的知识和理论,完善整个飞行器设计相关的知识体系、设计思路和流程。本篇及最基础的飞行力学开始,主要介绍以探空火箭为主的飞行器飞行过程中的力学概念和动力学模型。后续会逐步展开其他板块和内容。
1.绪论
飞行力学是一门研究飞行器的运动原理的学科。它研究飞行器如何在空气动力作用下实现控制和导航,如何在不同条件下,特别是在复杂气流环境中,确保飞行器有效地执行任务。针对不同的飞行器又包含不同的细分领域,如导弹飞行力学、火箭飞行力学、飞机飞行力学等等。
火箭飞行力学涉及火箭在太空中运动的力学原理,包括火箭的动力学、重力和阻力分析、升力产生和控制机制、外部参数和轨道计算等。火箭飞行力学研究的目的是了解火箭的运动特点,推导火箭在太空中运动的动力学方程,理解火箭的发射过程、导航过程和飞行控制的原理,以及火箭的发射数据和运行状态,为火箭发射建立一套完整的分析体系。
火箭飞行力学理论是火箭运动的基础理论,其动力学特性直接影响到控制系统的设计以及飞行弹道的稳定性。所以研究火箭运动过程中的飞行力学很有必要。
火箭在空间中飞行的动力学可分为质点动力学与姿态动力学,前者为长周期运动,后者为短周期运动。火箭的运动是多种运动的符合,包含火箭的刚体运动、壳体震动、推进剂变化引起的晃动等等。描述这三种运动的动力学方程分别是刚体动力学方程、弹性振动方程和推进剂晃动方程。对于一般的火箭,结构和质量分布基本是对称的,其动力学方程比较简单,但特殊设计的火箭动力学方程就比较复杂。
2.动力学方程的建立
针对低空发射的低海拔小尺寸探空火箭,我们忽略震动和推进剂变化,主要考察刚体运动方程。首先,在列方程之前首先需要若干个坐标系,这些坐标系为:
1)发射惯性坐标系(sa系)
2)发射坐标系(sg系)
3)平移惯性坐标系(s0系)
4)箭体几何坐标系(sb系)
5)箭体坐标系(s1系)
6)速度坐标系(sv系)
2.1一般方程
假定火箭结构不柔性,推进剂无流动,此时的箭体动力学为刚体动力学。首先研究质量不对称的动力学,及火箭质心与几何中心不重合的动力学。
把火箭上某质量单元dm的速度表示为:

其中v是sb系的速度矢量,r是质量dm到原点的矢量,w是sb系的角速度矢量
将上式在速度坐标系中展开:

质量元dm的加速度为:

箭体的运动方程为:

由静力学原理:

其中rbv是sb系原点到sv系原点的矢量

对以上所有公式列写方程组,并对全箭积分:


以上即力的平衡方程
为了推导力矩平衡方程,需要选取一个动点的角动量变化率的方程,选这个点为sb系原点
设火箭某质量元dm,相对ob系的矢量为rb,用ra表示动点ob到sa系的原点oa的矢量,那么绕oa点的角动量为:

对上式微分:

因为:

所以:

所以:

这就是对oa点的角动量微分公式
用Ma表示力矩:

由理论力学:

将公式代入两端:

即:

由几何关系:

代入上式:

用分量形式整理:

引用转动惯量和惯性积符号:

所以:

令:

对上式求微分:

整体代入:

整理后,得到力矩方程的分量形式:


整理力平衡方程和力矩平衡方程:

其中F是力的分量,M是力矩的分量,他们是由确定的力和干扰组成的,包括推力,控制力,空气动力,重力,发动机摆动惯性力。角标p,c,a,g,e,d分表代表以上力,d代表干扰。
从上式可以看出,火箭动力学方程是彼此相互交联的,非线性的。在后续设计控制系统的时候,需要对他们进行处理和设计,在是多数情况下,这些扰动量比较小的条件可以被忽略或线性化处理。
2.2简化刚体动力学方程
大多数火箭具有一下特点:
1)质量分布轴对称
2)飞行速度扰动是长周期运动,短时间内速度变化约等于0
3)火箭运动标准角速度很小,它们的二阶小量可以忽略
所以将平衡方程改写为扰动形式,进行线性化处理,忽略二阶小量:


对上式进行简化,引用以下符号代换:

可得:

上式分别描述了俯仰运动、偏航运动、滚转运动方程
2.3作用在火箭上的力和力矩
a.推力p
b.重力mg
c.控制力和控制力矩
控制力由操纵机构偏转产生,以操纵机构为摆动发动机为例,摆动的角度和推力影响火箭的姿态
d.空气动力
作用于火箭上的气动力实际为分布力,但在研究时,可将力集中至压力中心,并在速度坐标系分解为阻力、升力和侧向力。
e.操纵机构摆动的惯性力和力矩
f.干扰力和力矩
随机公差,发动机偏差,外界环境等均可造成误差和干扰
在实际飞行中,主要为风的干扰
2.4简化动力学方程
将力和力矩代入原方程并归一化处理:
俯仰运动方程:

偏航运动方程:

滚转运动方程:

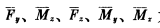
————————————————————————————————————————————————————
以上便是火箭飞行力学的基础核心理论,主要围绕动力学方程和运动学方程的推导展开,涵盖主要物理量和物理概念,需要一些大学物理的基础知识,后续结合这些理论,我们将展开飞行器控制的初步介绍,并开展对无控火箭飞行姿态的分析。
200字以内,仅用于支线交流,主线讨论请采用回复功能。