这篇帖子不涉及实物,主要目的就是介绍标题里那几个奇奇怪怪的名词,给想做轨道炮的朋友提供一个可能有效的、而且业余圈子里没人做过的思路。
帖子的顺序大概是:平顶电流脉冲是什么->怎么实现平顶电流脉冲(用脉冲形成网络)->怎么实现脉冲形成网络(用充电传输线)->怎么实现充电传输线
“平顶电流脉冲”就是字面意思,指电流波形有一个平顶的脉冲,峰值较低但持续时间较长。与之相对的,传统的“电容+续流二极管”得到的电流波形,就是一个“尖脉冲”,峰值很高但是持续时间很短。
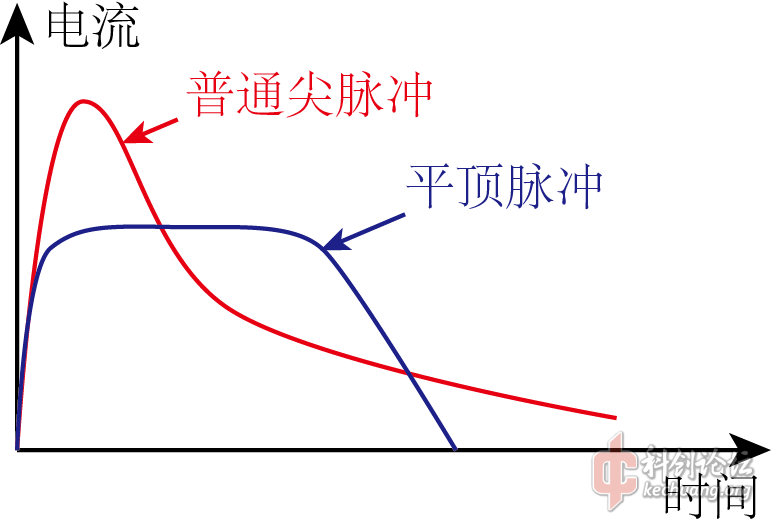
平顶电流脉冲的峰值较低,有利于减小烧蚀,降低机械应力。而且,在另一篇帖子中(https://www.kechuang.org/t/80745 ),我们指出过,只要总能量不变,不论电流的峰值和波形如何变化,轨道炮的效率都不变。所以平顶电流脉冲还不会降低轨道炮的加速性能,可以说是有百利而无一害。
用来形成某种特定形状的波形的网络,叫“脉冲形成网络”。由于这种平顶脉冲有很多优点,所以很多相关的研究都集中在这个方面。
最直观的思路就是,使用多组普通模块。每个模块都自带储能电容、开关、限流电感和续流二极管,单独一个模块输出的是普通尖脉冲。通过按特定时序触发这些模块,让这些普通尖脉冲相互叠加,可以非常灵活的得到各种波形。在职业研究人员的轨道炮中,这种做法非常常见。
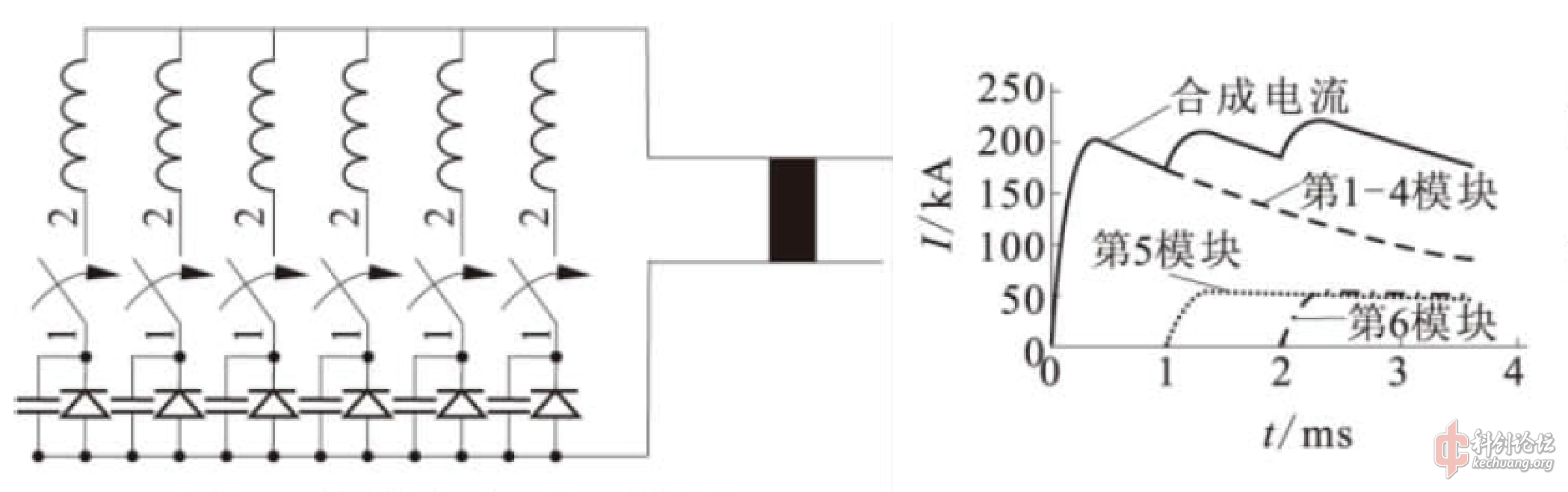
不过这种做法有点……贵。因为对时序有要求,所以基本只能使用半导体开关。因为每个模块都需要短时间承受近乎全部的电流,所以相应的开关和二极管功率容量还不能太小(当然因为导通时间短,所以功率容量可以稍小一些)。同时,在爱好者能承受的能量级别下,一堆小功率的元件,要比一个大功率的元件贵得多(功率容量越大的元件,每份功率的价格就越低)。总的来说就是各种贵,以至于对爱好者来说性价比很低。
另一种办法是,通过合理设计的无源器件网络(指电容和电感,出于效率要求一般不用电阻),自发的产生所需的波形。一般只需要使用一个开关,而且不需要精确的定时,可以用机械开关。比上面的方案便宜得多,也简单得多。
基于这种思路的最简单的一种网络,就是本篇帖子的主角:充电传输线。
传输线的概念,有点偏向于微波射频这些领域,有必要的话可以自行搜索了解。用一个高阻的充电电源,给传输线充上电,就得到了一根充电传输线,维基百科上有比较详尽的描述
https://en.wikipedia.org/wiki/Pulse-forming_network#Transmission-line_PFNs
这里做一个简单的翻译:
一个简单的“充电传输线型脉冲形成网络”如下图。它的结构就是一根长度为D的传输线(比如同轴线),左边接一个充电电源,其阻抗Rs远高于传输线的特征阻抗Z0,右边接一个开关和一个匹配负载RL(RL=Z0)。
![330px-Charge_line_animation.gif]()
使用时,先用充电电源给传输线充电至电压V,然后闭合开关。由于负载阻抗和传输线匹配,所以负载上的电压为V/2。同时传输线上的电荷开始向负载释放,形成一个向左传播的,幅度为V/2的电压阶梯。当它传播至最左端时,会被反射回来,产生向右传播的反射波。由于Rs≫Z0近似于开路,所以反射波的幅度也为V/2,且与入射波同向。反射波经过的地方,电压归零,当反射波传播至负载处时,整根传输线电压归零,放电完毕。
整个放电过程中,负载上的电压为一个幅度为V/2,持续时间为2D/c的理想方波脉冲,其中c为传输线中“光速”。在实际的系统中,由于传输线的损耗和色散,电压阶梯在传播过程中,会逐渐变平缓,造成方波的边沿,特别是下降沿变缓,减弱“平顶”的效果。后面的仿真里,可以比较明显的看到这个问题。
对于轨道炮来说,一般的传输线比如同轴线的储能显然是不够的。此时可以使用集总元件,比如电容和电感,来模拟传输线,如下图。
![集总元件模拟传输线.png]()
其中C1~C5为储能电容,被充电至450V;L1~L4是额外添加的电感,L5为轨道炮本身的电感;R1为轨道炮的电阻。
这种模拟传输线的特征阻抗计算公式为
L和C是每一小节的电感和电容,比如上图中,L=0.5uH,C=10mF,所以计算得到,这个模拟传输线的特征阻抗Z0=7.07mΩ。当R1= Z0=7.07mΩ时,仿真得到的电压和电流波形如下
![无耗模拟传输线的仿真波形.png]()
可以看到,轨道炮得到了一个幅度30kA左右,持续时间700us左右的平顶电流脉冲。同时在脉冲结束后,电容也放电到了接近0V。由于这里用有限数量的集总元件来模拟连续的传输线,会引入误差,所以这里的电流波形并不是一个理想的方形。不过至少比普通的尖脉冲要美观得多,如下图(这里是过阻尼RLC电路,所以图中加不加二极管对结果没有影响)
![理想电容,不使用PFN.png]()
当负载电阻R1小于特征阻抗时,一个脉冲不足以消耗完所有的能量。所以在第一个平顶脉冲后,会出现一个反向的脉冲。下图是R1=3.5 mΩ的结果。
![负载电阻较小.png]()
当R1大于负载电阻时,在第一个平顶脉冲后,会出现一个幅度更小,但方向相同的脉冲。如下图是R1=14 mΩ的结果。
![负载电阻较大.png]()
注意到,上面的仿真中,使用的是理想电容。如果是普通的电解电容,10mF时的内阻大约会是5mΩ。考虑内阻后的仿真结果如下
![考虑ESR时的PFN输出电流.png]()
可以看到,原本的高频波动被ESR所吸收,使得波形变得异常平滑。不过由于损耗增加,所以脉冲持续时间缩短,同时下降沿变缓。
上面的仿真中,没有考虑到轨道炮的弹丸移动。由于弹丸移动会导致电感和电阻升高,使电流下降。为了补偿这个因素,不考虑弹丸时,理想的电流波形应该是略有上升的平顶。这种波形可以通过减小远离负载端的传输线的特征阻抗,比如减小电感来实现,如下图
![略微上升的平顶脉冲.png]()
实际制作时,重点在于那几个电感(也没有别的东西了……)。上面仿真里的0.5uH电感是一个颇为尴尬的取值,大概就是刚好不适合用长直导线实现的电感量,需要用“线圈”的形式来实现。可以用金属板材,比如铝板切割成单层线圈,再分层组装起来。
![金属板制作线圈.jpg]()
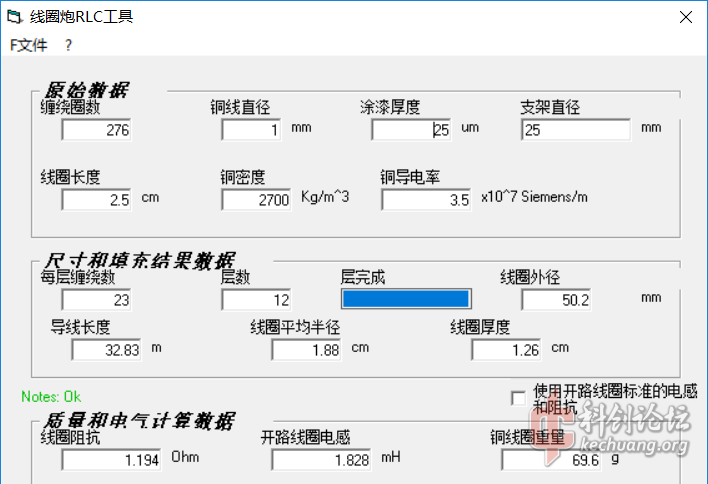
当然0.5uH不需要这么多匝数,大概只需要三四匝这种级别。具体需要的匝数可以用商用软件比如Maxwell算,或者用那个常见的模拟器来推算,如下。
![仿真线圈参数.png]()
在几何外形不变的情况下,线圈的电感和电阻,都与匝数的平方成正比。所以对于上面图里这样形状的线圈,可以算出来0.5uH的时候,需要“276匝*sqrt(0.5uH/1828uH)=4.56匝”,此时的电阻为0.33mΩ,可以忽略。不过可能受趋肤效应的影响非常显著,可能需要进一步的仿真来得到更精确的结果。












200字以内,仅用于支线交流,主线讨论请采用回复功能。