先介绍一下思路：首先求互感储能，然后根据“力是势能函数关于位移的负梯度”，求出电磁力。

我们的模型是普通的耦合电感，如下图。

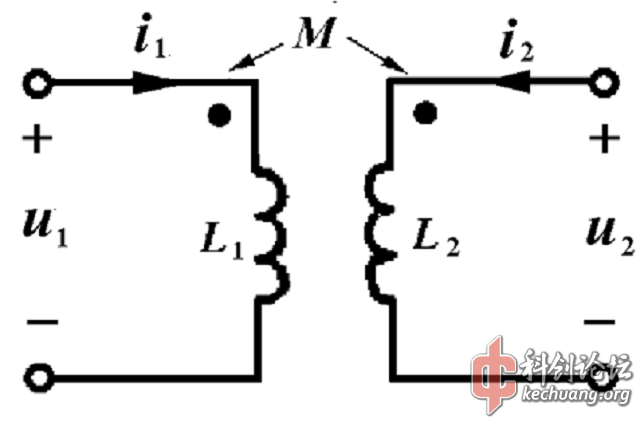
用 L1，L2 代表驱动线圈和弹丸线圈的自感，M 是它们之间的互感。这里我们认为 L1，L2 是固定不变的。

首先推导互感储能

由常识知
$$\{\begin{array}{r}{L}_1\frac{d{i}_1}{dt}+M\frac{d{i}_2}{dt}=u_1\\ M\frac{d{i}_1}{dt}+L_2\frac{d{i}_2}{dt}=u_2\end{array}$$
设从 t0 时刻到 t1 时刻，互感的能量变化为 ΔW，则有
$$\mathrm{\Delta }W={\int }_{t_0}^{t_1}(u_1{i}_1+u_2{i}_2)dt$$ 即 $$\mathrm{\Delta }W={\int }_{t_0}^{t_1}((L_1\frac{d{i}_1}{dt}+M\frac{d{i}_2}{dt})i_1+(M\frac{d{i}_1}{dt}+L_2\frac{d{i}_2}{dt})i_2)dt$$ 稍微整理一下得到
$$\mathrm{\Delta }W={\int }_{t_0}^{t_1}(L_1\frac{d{i}_1}{dt}{i}_1+L_2\frac{d{i}_2}{dt}{i}_2+(M\frac{d{i}_2}{dt}{i}_1+M\frac{d{i}_1}{dt}{i}_2))dt$$ 所以 $$\mathrm{\Delta }W={(\frac{1}{2}{L}_1{i_1}^2+\frac{1}{2}{L}_2{i_2}^2+M{i}_1{i}_2)|}_{t_0}^{t_1}$$
设互感储能为 W，且 i1 = i2 = 0 时 W = 0。 设t1时刻 i1 = i2 = 0，t0 时刻 i1 = i1(t0), i2 = i2(t0) 由上式知t0时刻互感储能满足 $$W(t_0)=-\mathrm{\Delta }W=\frac{1}{2}{L}_1{i_1}^2(t_0)+\frac{1}{2}{L}_2{i_2}^2(t_0)+M{i}_1(t_0)i_2(t_0)$$ 把上面的时间项去掉，就是大家喜闻乐见的互感储能公式了。

$$W=\frac{1}{2}{L}_1{i_1}^2+\frac{1}{2}{L}_2{i_2}^2+M{i}_1{i}_2$$

其中 i1, i2 的方向是同时流入同名/异名端。各符号含义参见开头的图。

然后求电磁力

设电磁力为 F，因为“力是势能函数关于位移的负梯度”所以有 $$F=-\frac{dW}{dx}=-(L_1{i}_1\frac{d{i}_1}{dx}+L_2{i}_2\frac{d{i}_2}{dx}+M{i}_1\frac{d{i}_2}{dx}+M{i}_2\frac{d{i}_1}{dx}+i_1{i}_2\frac{dM}{dx})$$ 下面我们来把F的表达式变成一个更方便的形式。
由常识知 $$\{\begin{array}{r}{L}_1{i}_1+M{i}_2={\phi }_1\\ M{i}_1+L_2{i}_2={\phi }_2\end{array}$$
把它们两边对 x 求导得 $$\{\begin{array}{r}{L}_1\frac{d{i}_1}{dx}+M\frac{d{i}_2}{dx}+i_2\frac{dM}{dx}=\frac{d{\phi }_1}{dx}\\ M\frac{d{i}_1}{dx}+L_2\frac{d{i}_2}{dx}+i_1\frac{dM}{dx}=\frac{d{\phi }_2}{dx}\end{array}$$
因为电感会试图使通过它的磁通量保持不变所以有$\frac{d{\phi }_1}{dx}=\frac{d{\phi }_2}{dx}=0$
所以 $$\{\begin{array}{r}{L}_1\frac{d{i}_1}{dx}+M\frac{d{i}_2}{dx}+i_2\frac{dM}{dx}=0\\ M\frac{d{i}_1}{dx}+L_2\frac{d{i}_2}{dx}+i_1\frac{dM}{dx}=0\end{array}$$
把 F 的表达式整理一下得到 $$F=-((L_1\frac{d{i}_1}{dx}+M\frac{d{i}_2}{dx}+i_2\frac{dM}{dx})i_1+(M\frac{d{i}_1}{dx}+L_2\frac{d{i}_2}{dx}+i_1\frac{dM}{dx})i_2-i_1{i}_2\frac{dM}{dx})$$ 所以线圈炮的电磁力满足

$$F=i_1{i}_2\frac{dM}{dx}$$

其中 i1, i2 的方向是同时流入同名/异名端。各符号含义参见开头的图。

本文的结论不适用于磁阻式，因为把磁阻式抽象成一个耦合电感是费力不讨好的。
另外有一点要注意，我们在开头引了一个条件“ L1，L2 是固定不变的”。所以这个结论也不完全适用于感应式，因为 L1，L2 是定值，要求电流的分布不发生变化。而对于普通的感应式（不使用线圈做弹丸），弹丸中的电流分布会随时间和弹丸位置的变化而变化。
另外自感是定值还要求驱动线圈和弹丸线圈都不会变形……

自感不变倒是比较适用于用线圈作为电枢的线圈炮，比如说发射线圈的感应式，或者分立驱动的有刷线圈炮。可惜这几样东西至今没见到有爱好者搞过……貌似本文的目标人群有点尴尬了……