序言：电磁炮要想走向小型化，实用化，充电的快速是必须要保证的一件事。有些新人在网上查阅资料时很可能会读到这样的句子：

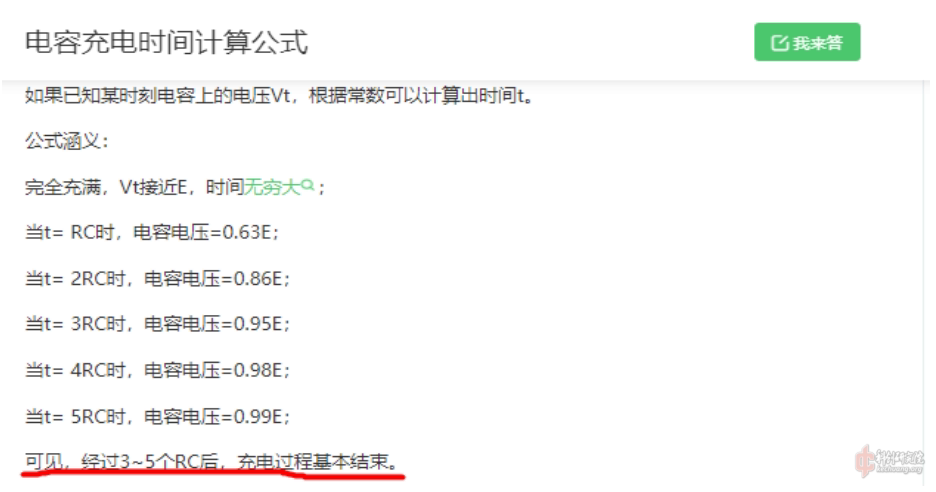
于是乎，他们就理所应当地使用有效电压等于目标电压的充电器，然后不耐烦地等上5个RC。甚至有些卖家在变压器选型时也会直接迎合最常见450V或400V的耐压。

实际上，在小型电磁枪充电电路中RC的值很大，比电容的ESR*C大得多，导致充到末尾电压上升得极慢。笔者认为，他们最大的问题在于混淆了目标电压与耐压之间的关系，过于迎合耐压而导致选择了非最优的电源电压。

本文旨在为大家定性地开拓思路并定量地分析一种特殊情况。

--------------------------我是分割线----------------------------------------

首先我们要假设一个由充电电路性质决定的条件：假设充电电路的短路功率是一个定值，并且在充电电路与储能电容之间没有其他元件。

定性地说，如果充电电压过于接近耐压，则虽然τ=RC中的R较小，但充电到末尾电路中的电流很小，导致电压上升很慢，很难达到目标电压；如果充电电压过高，则虽然充电到目标电压的整个过程中电压的上升速率变化不大，但是由于R很大，充电电流始终很小。我在使用高压包时对这个印象很深刻。电容的电压几乎是匀速上升的。

so，我们一定可以在这两个极端之间找到一个平衡使得充电到目标电压的时间最短。

下面，开始计算！用微分方程求解（假设这是个直流电源，电压等于真实交流源的有效值）

带入我们的约束条件减少变量的数量，得到最终表达式并寻找其极值：

最后这个方程以花体ε就是我们满足充电时间取得极值时的电源电压有效值。

可惜这是个超越方程，我不会解，于是只好请出卡西欧，用牛顿法尝试一下不带参量U的解。

下面是随意带入u值得到的一些解，为的是让大家清楚应该选怎样的充电电压。

将最后一个t-ε函数图像绘制在计算器中

趋势和我设想的一样，ε十分接近目标电压时曲线很陡，十分远离时也比较慢。

------------------我是分割线-----------------------------------

当然，P=Const这个条件只是为了方便，事实上，电压有效值比较小的充电电路往往能爆发出更大的短路功率。如果大家还有更好的想法，欢迎讨论，谢谢！