仿真的结果和 F=M*ΔΦ 计算的结果的差别,是因为计算中假设了“弹丸均匀一致磁化”,而仿真结果中并不是这样。仿真结果里是,弹丸离线圈近的时候磁化强度高,远的时候磁化强度低。
“弹丸均匀一致磁化”需要整个弹丸都处于深度磁饱和的状态。这需要线圈产生的磁场很强。可以试试在仿真里给电流加个零,这种情况下计算结果应该就和仿真结果基本一致了。
最近看到一本神书《你好,电磁炮》。书中推导出了计算磁阻炮的弹丸受力公式。即F = M · ΔΦ 。(图1)

图1:节选自013页
数据准备:
从公式中可以知道我们需要获取两个数据,一是磁化强度M。二是圆柱两端面的磁通量之差ΔΦ
1:获取磁化强度M
这部分比较容易,首先需要在maxwell里查询1010钢的磁化曲线。(图2)
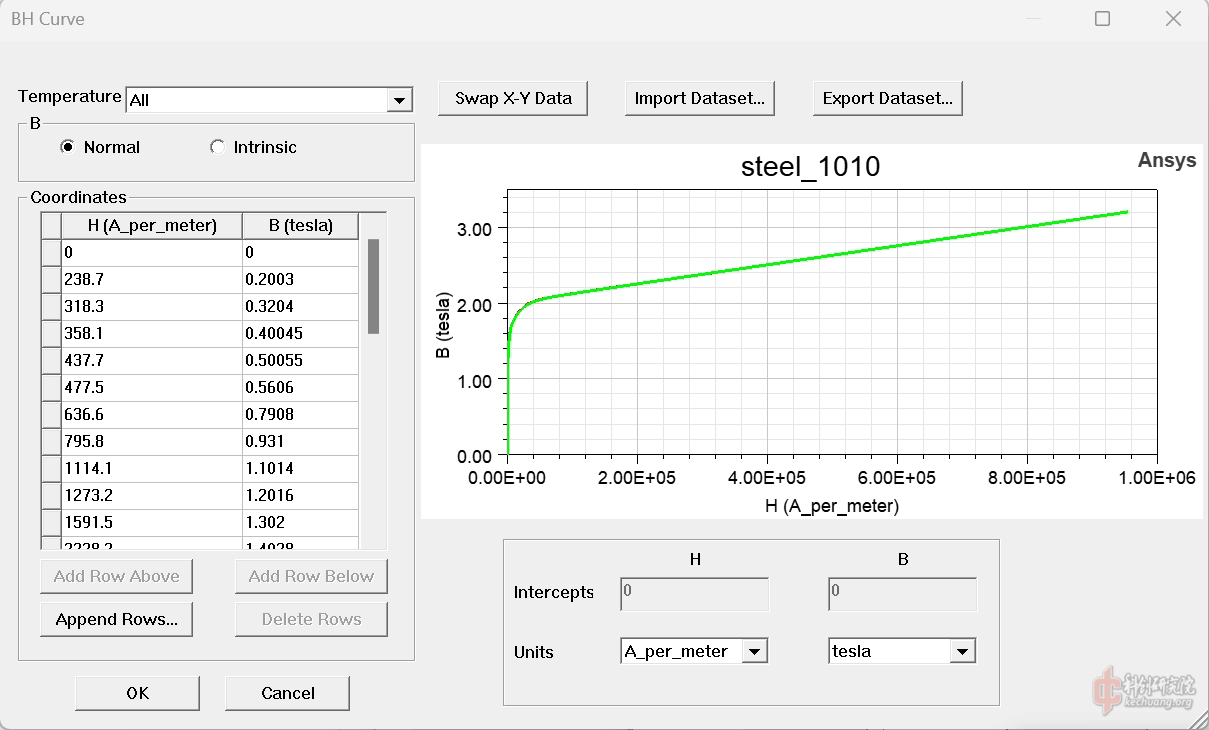
图2:1010钢的磁化曲线
使用M=B/μ0-H,和这个B-H曲线就可以算出M的值
2.获取 圆柱两端面的磁通量之差ΔΦ

ΔΦ = ΦR - ΦL,ΔΦ是圆柱两端面的磁通量之差。 磁通量这个数据较难直接获取,但是根据Φ=BS,只需在磁感应强度B上乘上S(这里指子弹的端面面积)。 所以现在我们需要知道 磁感应强度B的曲线。这里我们请出maxwell。
在mawell里solutiontype选择eddy current,画出线圈,参数为线圈长度8,内径8.5,外径18,匝数100,激励电流200A。再画出一条lines放置在线圈的中轴线上。(图3)。 然后点analyzeAll计算,结果选择create fields report,geometry选择我们画的那条直线Polyline1,计算结果选Mag_B。 即可计算出 线圈中轴线上的磁感应强度B曲线(图4)
![O5H{4WWEBBH0N`3PM0]8_AO.png](https://img.kechuang.org:81/r/354825?c=resource)
图3:线圈参数
![9P`5S{HP`3VLZUBDVG]X_C1.png](https://img.kechuang.org:81/r/354826?c=resource)
图4:磁感应强度B曲线
有了这条曲线,就很容易求出 ΔB即 圆柱两端面的磁感应强度之差,乘以S,即可求出ΔΦ。
编写程序与验证:
好了,有了以上的数据就可以写个python程序来验证下了。程序放在文末附件。
这次使用的弹丸的参数为:直径8,长度10。使用给定的线圈和弹丸参数,通过程序计算的受力曲线(即Force curve A)如图5所示。 同时,我们可以用maxwell直接计算出受力曲线(即Force curve B),如图6所示。

图5:根据磁感应强度曲线 计算出的受力曲线A

图6:maxwell直接计算出的受力曲线B
我们悲伤的发现,这俩曲线并不完全吻合,(不过抛开其他不谈,至少形状是对的

这里非常感谢三水大佬的指导,修正我关于M计算的错误后,新的计算结果和仿真结果仍有差距,似乎偏小。。。
结语:
F = M · ΔΦ ,这个公式计算出的弹丸受力大体上是正确的,但是想要用于磁阻炮的仿真计算上 还有待更进一步的研究。目前来说,用maxwell直接计算受力曲线 精度更高。
附件:
1:python代码 -修改了关于M的错误
2:计算磁感应强度B曲线的maxwell文件,和给出的result文件
3:直接计算受力曲线的maxwell文件,和给出的result文件
参考文献:
1:你好,电磁炮 ----潘永生,陶乐,刘虎编著
[修改于 1年0个月前 - 2024/06/18 23:49:08]
仿真的结果和 F=M*ΔΦ 计算的结果的差别,是因为计算中假设了“弹丸均匀一致磁化”,而仿真结果中并不是这样。仿真结果里是,弹丸离线圈近的时候磁化强度高,远的时候磁化强度低。
“弹丸均匀一致磁化”需要整个弹丸都处于深度磁饱和的状态。这需要线圈产生的磁场很强。可以试试在仿真里给电流加个零,这种情况下计算结果应该就和仿真结果基本一致了。
回复1楼评论中的内容:
我程序的计算是对弹丸区域进行了细分的,分割了100份,也遵循了弹丸离线圈近的时候磁化强度高的现实。。。
这个细分是不对的。弹丸上某个点的磁感应强度,不仅取决于线圈的磁场强度,还取决于弹丸上其他部分的磁化强度。你细分的方式,是考虑不到弹丸各点之间的相互影响的(也可以称之为“弹丸导磁”)。不过你的主要问题应该不是这个,因为这个问题会导致计算结果偏小。
现在只能怀疑是磁化曲线有问题,因为到2.4T后磁化数据是缺失的,超过的部分是外插的结果(线性增长)。电流加个0后,算出的磁导为20T,远大于通常说的深度磁饱和。。。。。
这个是你的主要问题,但是具体出问题的点和你想的不太一样。问题在于你和磁化强度求错了。磁感应强度(B),磁场强度(H),磁化强度(M)之间的关系是
关于磁饱和,你应该是被“饱和磁感应强度”这个词给误导了。磁感应强度B实际上是永远不会饱和的,铁芯里的磁感应强度可以升到任意高,几十几百T都可以,只有磁化强度M会饱和。参考这篇帖子以及我在下面的回复:
https://www.kechuang.org/t/85224
200字以内,仅用于支线交流,主线讨论请采用回复功能。