电树枝物理现象的仿真研究
一、 NPW模型-圆形电极
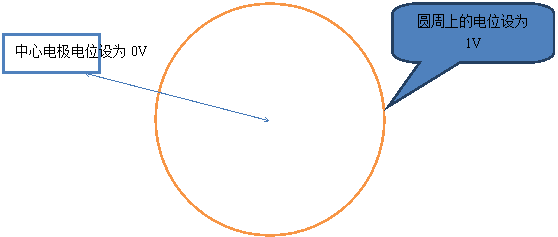
放电发展遵循如下规则:
(1)“步进式”发展模式;放电树枝的发展是按步进行的;
(2)每一步中,点与点之间只有一条连接线被加到放电树枝中,具体哪两点之间进行连接由步骤(3)中的发展概率函数决定。
(3)放电树枝由黑结点向周围发展时,电树向各个方向发展的概率可看成是此结点与周围各结点之间电位梯度的函数。设点的坐标为(i, k),虚点的坐标为(i’ , k’ )。则黑点向虚点发展的概率为
![image002.png]()
各节点的电位可由拉普拉斯方程计算得到
![image007.gif]()
通过有限差分法来求解计算域内的电位分布。
结果
(1)η=0.5时,放电后电位图及树枝形状如下图,计算得放电树枝的分形维数D=1.9388
![image009.gif]()
(2) η=1时,放电后电位图及树枝形状如下图,计算得放电树枝的分形维数D=1.7132
![image011.gif]()
(3) η=1.5时,放电后电位图及树枝形状如下图,计算得放电树枝的分形维数D=1.4974
![image013.gif]()
二、 WZ模型-针板电极
WZ模型简介
在NPW模型上做了两方面的改进:首先引入了临界场强Ec这一参数,只有树枝所处局部场强大于Ec时,树枝才能向周围发展;第二,在介质放电时,树枝上各点电位不为零,放电发展时内部压降位Us*s(Us为单位树枝内压降,s为树枝长度)。
边界条件如第一章
(1) η=0.5,K=0.001(K=phi_i/phi_c phi_i为外电极处电压,phi_c为单位长度内临界放电电压差), phi_S=0.0001时,放电后电位图及树枝形状如下图,计算得放电树枝的分形维数D=1.8317
![image015.gif]()
(2) η=1.0,K=0.001(K=phi_i/phi_c phi_i为外电极处电压,phi_c为单位长度内临界放电电压差), phi_S=0.0001时,放电后电位图及树枝形状如下图,计算得放电树枝的分形维数D=1.7658
![image017.gif]()
(3) η=1.5,K=0.001(K=phi_i/phi_c phi_i为外电极处电压,phi_c为单位长度内临界放电电压差), phi_S=0.0001时,放电后电位图及树枝形状如下图,计算得放电树枝的分形维数D=1.6216
![image019.gif]()
(4) η=0.5,K=0.005(K=phi_i/phi_c phi_i为外电极处电压,phi_c为单位长度内临界放电电压差), phi_S=0.001时,放电后电位图及树枝形状如下图,计算得放电树枝的分形维数D=1. 9112
![image021.gif]()
(5) η=1.0,K=0.005(K=phi_i/phi_c phi_i为外电极处电压,phi_c为单位长度内临界放电电压差), phi_S=0.001时,放电后电位图及树枝形状如下图,计算得放电树枝的分形维数D=1. 6996
![image023.gif]()
(6) η=1.5,K=0.005(K=phi_i/phi_c phi_i为外电极处电压,phi_c为单位长度内临界放电电压差), phi_S=0.001时,放电后电位图及树枝形状如下图,计算得放电树枝的分形维数D=1. 6355
![image025.gif]()
三、 NPW模型-针板电极
![image026.gif]()
Note: 该模型的边界条件设置的合理性有待商榷;
更为合理的边界条件应为“在其他边界满足:![image027.png]() =0”,即表示在边界上没有电荷存在。
=0”,即表示在边界上没有电荷存在。
结果
(1)η=0.5时,放电后电位图及树枝形状如下图,计算得放电树枝的分形维数D=1.8554
![image030.gif]()
![image030.gif]()
(2)η=1.0时,放电后电位图及树枝形状如下图,计算得放电树枝的分形维数D=1.5952
![image032.gif]()
(3)η=1.5时,放电后电位图及树枝形状如下图,计算得放电树枝的分形维数D=1.4606
![image034.gif]()
四、 WZ模型-针板电极
WZ模型简介
在NPW模型上做了两方面的改进:首先引入了临界场强Ec这一参数,只有树枝所处局部场强大于Ec时,树枝才能向周围发展;第二,在介质放电时,树枝上各点电位不为零,放电发展时内部压降位Us*s(Us为单位树枝内压降,s为树枝长度)。
边界条件如第三章
(7) η=0.5,K=0.001(K=phi_i/phi_c phi_i为放电电极处电压,phi_c为单位长度内临界放电电压差), phi_S=0.0001时,放电后电位图及树枝形状如下图,计算得放电树枝的分形维数D=1.6180
![image036.gif]()
(8) η=1.0,K=0.001, phi_S=0.0001时,放电后电位图及树枝形状如下图,计算得放电树枝的分形维数D=1.5171
![image038.gif]()
(9) η=1.5,K=0.001, phi_S=0.0001时,放电后电位图及树枝形状如下图,计算得放电树枝的分形维数D=1.3668
![image040.gif]()
一、 NPW模型-圆形电极

放电发展遵循如下规则:
(1)“步进式”发展模式;放电树枝的发展是按步进行的;
(2)每一步中,点与点之间只有一条连接线被加到放电树枝中,具体哪两点之间进行连接由步骤(3)中的发展概率函数决定。
(3)放电树枝由黑结点向周围发展时,电树向各个方向发展的概率可看成是此结点与周围各结点之间电位梯度的函数。设点的坐标为(i, k),虚点的坐标为(i’ , k’ )。则黑点向虚点发展的概率为
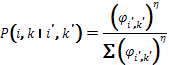
各节点的电位可由拉普拉斯方程计算得到
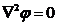
通过有限差分法来求解计算域内的电位分布。
结果
(1)η=0.5时,放电后电位图及树枝形状如下图,计算得放电树枝的分形维数D=1.9388
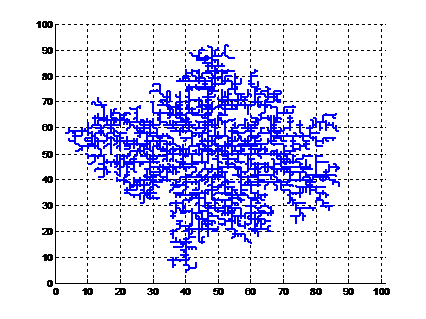
(2) η=1时,放电后电位图及树枝形状如下图,计算得放电树枝的分形维数D=1.7132
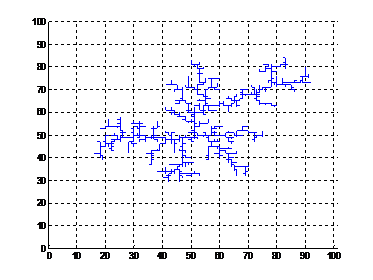
(3) η=1.5时,放电后电位图及树枝形状如下图,计算得放电树枝的分形维数D=1.4974
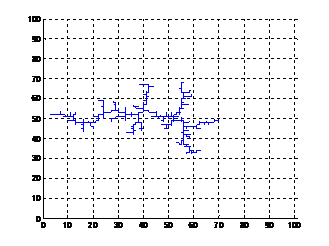
二、 WZ模型-针板电极
WZ模型简介
在NPW模型上做了两方面的改进:首先引入了临界场强Ec这一参数,只有树枝所处局部场强大于Ec时,树枝才能向周围发展;第二,在介质放电时,树枝上各点电位不为零,放电发展时内部压降位Us*s(Us为单位树枝内压降,s为树枝长度)。
边界条件如第一章
(1) η=0.5,K=0.001(K=phi_i/phi_c phi_i为外电极处电压,phi_c为单位长度内临界放电电压差), phi_S=0.0001时,放电后电位图及树枝形状如下图,计算得放电树枝的分形维数D=1.8317

(2) η=1.0,K=0.001(K=phi_i/phi_c phi_i为外电极处电压,phi_c为单位长度内临界放电电压差), phi_S=0.0001时,放电后电位图及树枝形状如下图,计算得放电树枝的分形维数D=1.7658

(3) η=1.5,K=0.001(K=phi_i/phi_c phi_i为外电极处电压,phi_c为单位长度内临界放电电压差), phi_S=0.0001时,放电后电位图及树枝形状如下图,计算得放电树枝的分形维数D=1.6216

(4) η=0.5,K=0.005(K=phi_i/phi_c phi_i为外电极处电压,phi_c为单位长度内临界放电电压差), phi_S=0.001时,放电后电位图及树枝形状如下图,计算得放电树枝的分形维数D=1. 9112

(5) η=1.0,K=0.005(K=phi_i/phi_c phi_i为外电极处电压,phi_c为单位长度内临界放电电压差), phi_S=0.001时,放电后电位图及树枝形状如下图,计算得放电树枝的分形维数D=1. 6996

(6) η=1.5,K=0.005(K=phi_i/phi_c phi_i为外电极处电压,phi_c为单位长度内临界放电电压差), phi_S=0.001时,放电后电位图及树枝形状如下图,计算得放电树枝的分形维数D=1. 6355

三、 NPW模型-针板电极

Note: 该模型的边界条件设置的合理性有待商榷;
更为合理的边界条件应为“在其他边界满足:
 =0”,即表示在边界上没有电荷存在。
=0”,即表示在边界上没有电荷存在。
结果
(1)η=0.5时,放电后电位图及树枝形状如下图,计算得放电树枝的分形维数D=1.8554


(2)η=1.0时,放电后电位图及树枝形状如下图,计算得放电树枝的分形维数D=1.5952

(3)η=1.5时,放电后电位图及树枝形状如下图,计算得放电树枝的分形维数D=1.4606

四、 WZ模型-针板电极
WZ模型简介
在NPW模型上做了两方面的改进:首先引入了临界场强Ec这一参数,只有树枝所处局部场强大于Ec时,树枝才能向周围发展;第二,在介质放电时,树枝上各点电位不为零,放电发展时内部压降位Us*s(Us为单位树枝内压降,s为树枝长度)。
边界条件如第三章
(7) η=0.5,K=0.001(K=phi_i/phi_c phi_i为放电电极处电压,phi_c为单位长度内临界放电电压差), phi_S=0.0001时,放电后电位图及树枝形状如下图,计算得放电树枝的分形维数D=1.6180

(8) η=1.0,K=0.001, phi_S=0.0001时,放电后电位图及树枝形状如下图,计算得放电树枝的分形维数D=1.5171

(9) η=1.5,K=0.001, phi_S=0.0001时,放电后电位图及树枝形状如下图,计算得放电树枝的分形维数D=1.3668



200字以内,仅用于支线交流,主线讨论请采用回复功能。