其实最开始我也钟意磁阻式，但让我真正开始对感应炮感兴趣的是一段视频，XXXXXXXXXXXXXXXX/x/page/XXXXXXXXXXXXXXml。

这个视频标题是《21mm口径感应线圈炮》，看视频中，一枚贰分硬币 ，能把易拉罐击爆，

我后来用扁皮弹弓试了下，至少需要100mps左右的初速度才可以达到这个效果，这个可是单级的效果。

一毛硬币重量大约2.2g，11joule的存能。

-

论坛常见的是磁阻炮，而感应炮见的很少，详见badboyfly和三水合番以及M版主的帖子。

实验贴也只有寥寥无几，国外爱好者玩得也真的少，我就把这个帖子作为这段时间无聊实验的一个记录，

作为对较少见平板线圈炮分析的一个理论设计与实验补充，也给大家带来一些funny。

-

我查阅了一些文献，《电炮原理》就是其中很有用的文献，还有很多paper描述了感应电磁炮的模型。

感应线圈炮其实是最有潜力的一种电炮种类，它无需受到磁阻那样最多2T饱和磁场的材质限制，

所以发射推力在材料强度限制内，几乎可以认为是无限大的，并且效率理论上可达100%，不存在拓扑限制。

实际科学家们做出的模型，可以达到45%的效率。

-

书里面的公式我跟着用笔推了一遍，很晦涩，

我建立了一个基本的知识体系后，想用高中物理和数学知识描述一下感应线圈炮的设计。

感应电磁炮可以用电流丝模型来分析，其运动模型简单来说用能量守恒定律来描述。

简单来讲就是，理想状态下，认为弹丸和线圈是由无限个下图的电流丝组成的，

设定两个电感L1，L2分别是工作线圈、L1固定，L2可以被发射出去，他们之间有各自的自感、互感。

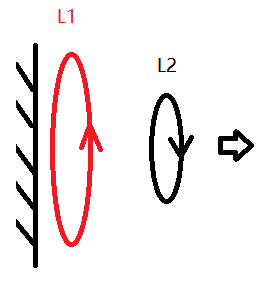
总能量Wsum=WL1+WL2

两个电感的能量可以认为是动能和电能的和，而L1是固定的，所以有WL1=EL1

而L2是电枢，则有WL2=EL2+KL2,KL2是动能。

Wsum=EL1+EL2+KL2

L1和L2之间是有互感的，这个互感定义为M，互感的能量以两个电感的耦合变化量存在，以磁场的形式储存能量。

这个计算方法也是1/2I1I2M12，1/2I1I2M21，有M12=M21，We=I1I2M。

Wsum=EL1+EL2+KL2+I1I2M。

-

从上面这个公式可以发现规律，实际上两个线圈（弹丸和线圈）之间的互感储存的能量是系统输出的动能。

这个规律非常重要，在设计电炮中经常用到，可以广泛应用于包括轨道炮在内的有电感变化的电炮分析。

-

而牛顿第二定律可知，力量矢量与方向的积是力量的做功。

而把I1I2M=KL2对位移dx微分，得到的就是F=dW/dx=d（I1I2M）/dx，这个公式就是弹丸在发射时候的受力情况。

由于I与位移dx可以认为无关，当作常量微分，所以能够得到F=I1I2dM/dx（著名的感应炮公式）。

-

可以看见F（I1，I2 ，dM/dx，）有三个相关参数，

分别是线圈电流、弹丸（电枢）电流，以及dM/dx，前两个参数从直觉上很好理解。

线圈电流大，所以能量大，受力就大，弹丸感应出来的电流大，安培力就大，也很好理解。

其实在耦合度不变的情况下，I1和I2是满足正相关的，可以近似认为I2=K（M）I2。

但dM/dx怎么去理解它？

-

dM/dx从数学意义上看，就是互感在距离上的微分，物理意义就是随着距离变化的互感变化量。

这样一来，就很好理解了

由于互感是由线圈形状与弹丸形状决定的，由之间的耦合度决定，所以受力的大小除了电流大小之外，

还与弹丸离开线圈，互感减小的速度有关，这个量被称为互感梯度。

从这张图里面，可以看出两个线圈之间的互感，当两者完全重合时候，互感达到最大。

而互感梯度就是互感的对dx的微分，也就是变化率，在大约为线圈总长1/4的位置，能获得最大的加速力。

而在线圈总长1/2的位置，是我们设计的可利用加速区间，此时电磁力符号不变化。

理论上可以认为感应线圈炮是不存在回拉的。

-

但是天底下没十全十美的事，实际上弹丸是在运动中的，我们拿出祖传LTspice做一个电路仿真

把不同耦合下的波形画出来

可以看到，随着耦合度的减小，弹丸电流提前过零，变成与励磁电流相同。

此时根据楞次定律，是相互吸引的关系，这样会产生一个吸引力。这个区间就会让弹丸速度变慢，

那么怎么用高中物理理解呢？

可以想象弹丸是一个导体，在磁场中向前运动，会产生动生电流，和感生电流在过零点相互抵消。

-

如何解决这个问题？

回到前面的电感梯度上来，只需要让弹丸在加速区，尽快的脱离耦合区域，就可以让回拉变得很小。

用ansoft Maxwell为硬币弹射模型建立一个field，在仿真后给出磁力线分布，可见当距离15mm时，磁场影响几乎降低一个数量级。

而电容对线圈的放电，是可以通过过1/2pi*sqrtLC来计算振荡周期。

所以一个设计良好的单级感应电磁炮，是需要让LC放电半周期时，弹丸刚刚脱离“耦合区域”。

1：由于我们希望设计单级尽可能高速度的感应炮，所以放电周期不能很大。

2：这就要求小L和小C的组合，这样唯一的选择就是高电压驱动。

3：考虑到尽快脱离“耦合区域”，这样会要求最开始弹丸就处于电感梯度峰值。

-

综合以上3点，单级感应电磁炮为了达到尽可能高的效率，遵循公式W=MI1I2，F=dM/dxI2I1。

既需要更快的让弹丸脱离，又需要更多的利用整段加速区。

而平板线圈的结构，在初始耦合度接近于0.9，而随着距离的衰减，互感衰减很快，这样就很符合我们对单级线圈炮的定义。

这样意味着整体能量利用效率会很高，并且由于电感梯度很大，加速会很“急”。

-

软件仿真中，设定800V 360uF的电容储能，瞬间的峰值推力可以超过2.8KN，而仅仅持续40us。

以上这两点其实在很多爱好者的实验中，能得到证明，往往发射几次，木质桌面都被打出凹痕，线圈也开胶。

我自己也做了相关实验，用502加水雾固化的线圈用手都掰不动，发射三四次，直接散架。

这一点和线圈间电磁力关系不大，而是由于撞击导致的损坏。

-

接下来利用软件对弹丸仿真，参数仿真功能能够很好的得出最佳值。

扫描5-25圈，发现最佳值出现在16T和22T，分析取前面的值。

从图中可以见到很有意思的现象是，随着匝数加大，速度降低了。

22T是电流和互感梯度的均衡，后者由于回拉，表现出16T一致的初速度，约为130mps。

考虑实际电阻影响，取16T较为合理，。

-

动手做实验

-

各种匝数的线圈实际对比过，和仿真结果基本吻合，确实是匝数多的那个线圈威力最大。

打软木板，能够留下清晰的痕迹，用弹道摆估测过发射的速度大约100mps，后来这个木板被我打散架了。

这个数据比仿真给出的低不少，可能是因为电阻的影响。

但是效果依然不可忽视，大约115J的储能 11J的动能，此时的单级效率约为10%，这超过了很多多级磁阻。

后面我用这台实验炮打了易拉罐，效果和视频一样（懒得录视频了，按我参数自己去测试）

另外我用一个塑料手电的光杯作为目标物，结果一样很炫酷，直接把塑料材质的光杯带着外壳打的粉碎。

-

实验结果可以见的，这种平板线圈是非常适合作为发射硬币的，感谢发明这种结构的爱好者（我不知道是谁，因为很多书上根本没有这种结构）

这种结构既能够满足高能量利用率，又能满足电感梯度，确实是非常有趣的结构，我建议大家都可以尝试一下。

唯一的几个不足的就是，

我现在几乎无法找到能够让线圈不报废的方法，不管胶多厚，发射几次，线圈必然散架GG

另外一个问题就是不知道怎么固定弹丸，只能垂直放在线圈上面，导致我家的天花板直接遭殃，这就是打碎手电光杯撞到天花板的效果。

把我烦死了，有盆友知道怎么弄的顺带告诉我一下，

-

最后就是，一定一定注意安全，这个威力很大，而且没有炮管导向，方向很随机，11J打到眼睛就完蛋。

所以还是要做好安全防护。

enjoy it