好高级的计算器啊！[s:275]。。。。。。。公式有点类似轨道炮计算电容放电时间的公式。。
58077
%7B%22isLastPage%22%3Atrue%2C%22notes%22%3A%5B%5D%2C%22pid%22%3A%22t58077%22%2C%22tid%22%3A%2258077%22%2C%22mainForumsId%22%3A%5B%22139%22%5D%2C%22categoriesId%22%3A%5B%22437%22%5D%2C%22tcId%22%3A%5B%5D%7D
%7B%22isEditMode%22%3Afalse%7D
关于SGTC主电容工作后放电时间的一点理论计算
这几天闲的蛋疼花了一堆时间来算这个= =就为了算出TC主电容过多久了可以碰。不清楚其他KCer有没有进行过类似的研究。本人高中生知识水平所限所以方法可能很笨拙……
假设电源断开后主电容C正好充至额定电压E，此时火花隙断开，电容C和泄放电阻R形成回路放电
一开始很天真的用W=UURt=CUU/2得出t=CR/2的，后来才想起来放电过程中电压和电流都是逐渐减小的，遂予以否定
接下来又发现U、I与t的关系还不是简单的正比例关系，而是一条导数减速递增的减函数(恕我语死早只能这么表达……)(如图)，表达式还是未知的
![it.png]()
![ut.png]()
然后纠结了好久，总算在I-t图像找到了突破口
![it积分.png]()
如图，对I-t图像进行积分，可以得到电荷量Q，电容电压从E降至人体安全电压36V所需时间为t0.
现在将t0平均分割成n份，每份时间为T，假设每个T内电容储有的电荷量不变
初始电荷量为Q0，放电电流I0=E/I=Q0/(C*R)
经过T时间后剩余电荷量Q1=Q0-I0*T=Q0*(1-T/(C*R))
同理，2T时刻剩余的电荷量Q2=Q1*(1-T/(C*R))=Q0*(1-T/(C*R))^2
以此类推，经过t0=n*T时间，剩余电荷量Qn=Q0*(1-T/(C*R))^n
整理，得
![QQ拼音截图未命名.png]()
当n趋近于正无穷时，T*n趋近于t0
现在画出该函数的大致图像，可以看到函数切线的斜率不断逼近0
![IMG0629004600.jpg]()
来看一组数据(以C=15nF,R=50MΩ为例)
![K.png]()
![IMG0629004400.jpg]()
假设电源断开后主电容C正好充至额定电压E，此时火花隙断开，电容C和泄放电阻R形成回路放电
一开始很天真的用W=UURt=CUU/2得出t=CR/2的，后来才想起来放电过程中电压和电流都是逐渐减小的，遂予以否定
接下来又发现U、I与t的关系还不是简单的正比例关系，而是一条导数减速递增的减函数(恕我语死早只能这么表达……)(如图)，表达式还是未知的
然后纠结了好久，总算在I-t图像找到了突破口
如图，对I-t图像进行积分，可以得到电荷量Q，电容电压从E降至人体安全电压36V所需时间为t0.
现在将t0平均分割成n份，每份时间为T，假设每个T内电容储有的电荷量不变
初始电荷量为Q0，放电电流I0=E/I=Q0/(C*R)
经过T时间后剩余电荷量Q1=Q0-I0*T=Q0*(1-T/(C*R))
同理，2T时刻剩余的电荷量Q2=Q1*(1-T/(C*R))=Q0*(1-T/(C*R))^2
以此类推，经过t0=n*T时间，剩余电荷量Qn=Q0*(1-T/(C*R))^n
整理，得
当n趋近于正无穷时，T*n趋近于t0
现在画出该函数的大致图像，可以看到函数切线的斜率不断逼近0
来看一组数据(以C=15nF,R=50MΩ为例)
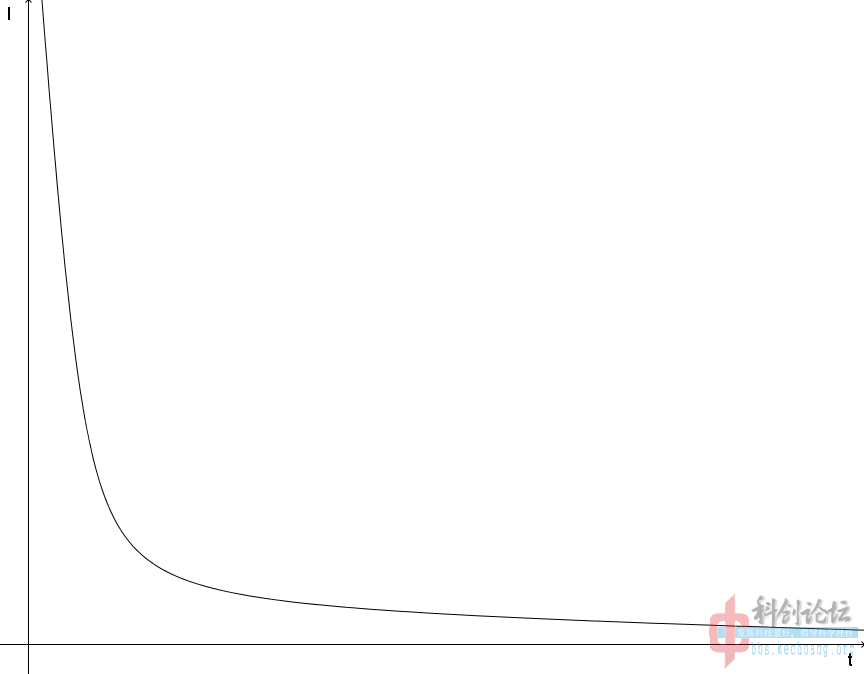
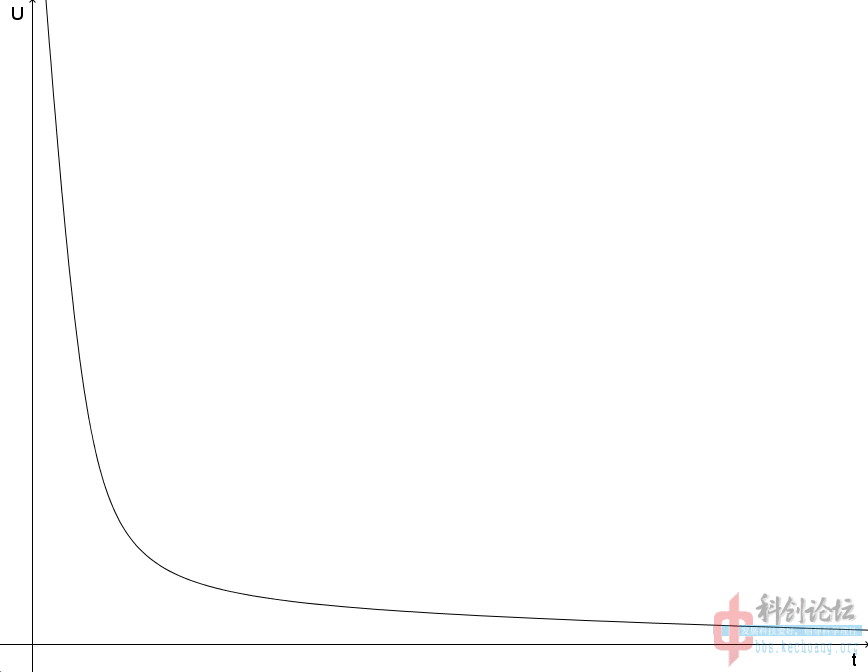
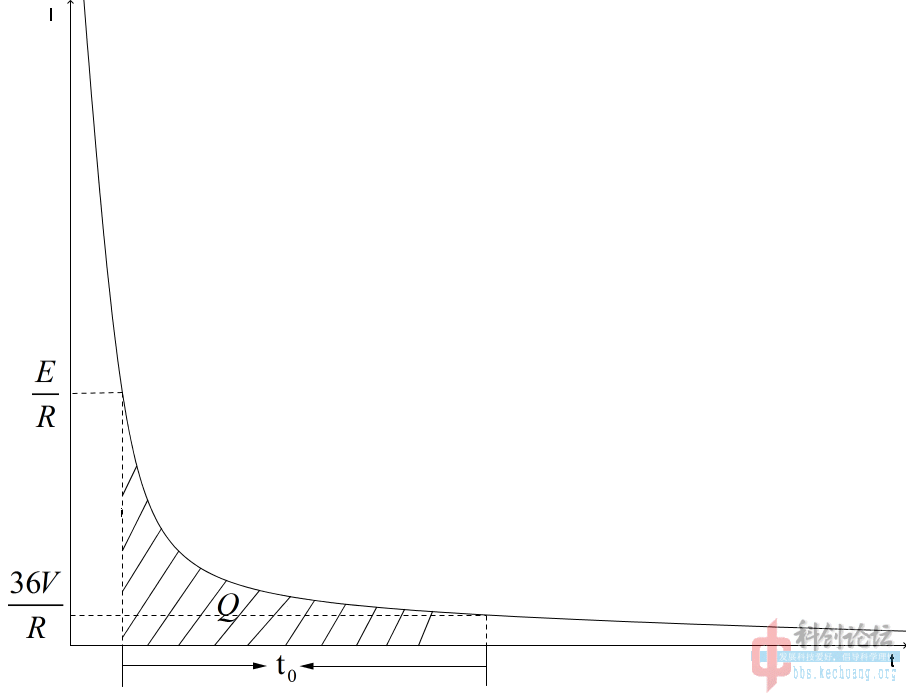
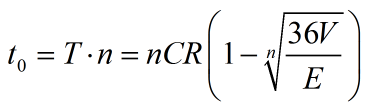
| n\T*n/E | 5000V | 10000V | 20000V | 30000V | 50000V |
| 10 | 2.920748324s | 3.22740711s | 3.513529874s | 3.671934255s | 3.8625711s |
| 1000 | 3.691142755s | 4.208265393s | 4.725029714s | 5.027151466s | 5.407605495s |
| 10000 | 3.699343047s | 4.218929006s | 4.738478951s | 5.042379492s | 5.425231354s |
| 100000 | 3.700164412s | 4.219997348s | 4.739826681s | 5.043905678s | 5.426998151s |
可以看到当n=10000时，计算值的误差已经可以减小到0.01s内，可以满足一般的精度要求了
但是很明显n取10000没有计算器或者电脑的话基本没法算……计算量实在太大，那么要怎么减小计算量呢？
令f(n)=T*n，定义常数K，使得K*f(2)=f(10000)，这样就能大大减少计算量了
K与E的关系如下
图像如下
接着是一组对照表数据，可以根据自己的主电容大致的电压范围取K值求t0的近似值
| E | 5000V | 10000V | 20000V | 30000V | 50000V | 100000V | 200000V | 500000V |
| K | 2.694898411 | 2.992148231 | 3.298948499 | 3.482213751 | 3.716546305 | 4.039781251 | 4.368021839 | 4.80794497 |
以上都是个人的理论，没有能力进行相关实验，欢迎有兴趣的KCer对此进行验证
回 2楼(rudolf) 的帖子
…好吧我在之前没去百度过，找到了，和这个的计算结果出入不大。那个公式的推导需要用到高数吧？
引用
加载评论中，请稍候...
200字以内，仅用于支线交流，主线讨论请采用回复功能。
回 楼主(左凌子) 的帖子
为何要计算过多久时间可以碰。。
楼主有没有听过拖尾无限原理 那后面一段低压区实际上是很长很长的
楼主有没有听过拖尾无限原理 那后面一段低压区实际上是很长很长的
引用
加载评论中，请稍候...
200字以内，仅用于支线交流，主线讨论请采用回复功能。
回 4楼(rb-sama) 的帖子
SGTC工作完电源断开后不是会储有电能么，只是想计算一下关机多长时间后电容内蓄有的电能不再具有危险性
原理没听过…是不是就是无限趋近于0？
原理没听过…是不是就是无限趋近于0？
引用
加载评论中，请稍候...
200字以内，仅用于支线交流，主线讨论请采用回复功能。
引用
加载评论中，请稍候...
200字以内，仅用于支线交流，主线讨论请采用回复功能。
左凌子妹纸辛苦了，好东西大家分享，最近做多大的傻瓜兲(王八)朝啊？rb萨满说得没有错，有点无限低压区，不过那个时候用手摸已经没有影响了。不过有的电容时间长了还保留着高压，，摸起来很爽的。。。单个电容并联兆欧电阻吧。。。
引用
加载评论中，请稍候...
200字以内，仅用于支线交流，主线讨论请采用回复功能。
兰若，公主魂 发表于 前天 19:14
左凌子妹纸辛苦了，好东西大家分享，最近做多大的傻瓜兲(王八)朝啊？rb萨满说得没有错，有点无限低压区，不过那个时候用手摸已经没有影响了。不过有的电容时间长了还保留着高压，，摸起来很爽的。。。单个电容并
高三了没空，而且旧的那个还在故障呢
引用
加载评论中，请稍候...
200字以内，仅用于支线交流，主线讨论请采用回复功能。